La giunzione Schottky Rev1

CAPITOLO IV
La giunzione Schottky
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-1
IV.1 Formazione della giunzione
La giunzione Schottky è l’elemento costituente di praticamente tutti i dispositivi elettronici. Infatti per
polarizzare il dispositivo ed iniettare una corrente elettrica è sempre necessario realizzare piazzole di
contatto elettrico.
Il trasporto di corrente tra questi due materiali dipende strettamente dalle bande di energia e dalla loro
occupazione.
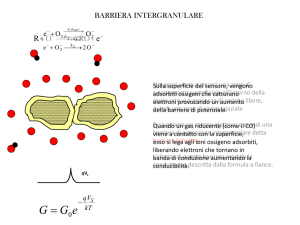
In generale quando si realizza la giunzione tra un metallo ed il semiconduttore si forma una barriera di
energia sia per gli elettroni che per le lacune.
Per valutare questa barriera è necessario conoscere alcuni parametri fisici del metallo e del
semiconduttore:
•
La funzione di lavoro del metallo
•
La funzione di lavoro del semiconduttore
•
L’affinità elettronica del semiconduttore
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-2
Quando si uniscono i materiali, come avveniva per la giunzione p-n, si ha diffusione dei portatori
seguita da una deriva per la formazione di un campo elettrico intrinseco.
L’andamento della corrente tra i due materiali, a causa di questa barriera, non è lineare.
In polarizzazione diretta della giunzione si ha
Mentre in polarizzazione inversa
Nei casi particolari in cui l’andamento della corrente è lineare il contatto è detto Ohmico. Ciò si
ottiene o perché l’altezza della barriera e ridottissima (si ha solo per poche coppie di metallosemiconduttore) o perché la barriera è talmente sottile che viene attraversata per tunnelling.
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-3
(si ottiene drogando pesantemente il materiale semiconduttore).
L’altezza della barriera in prima approssimazione si può scrivere:
φB = φM − χ S
In una giunzione ad esempio tra oro e silicio come in figura
q χ Silicio ≅ 4.15 eV
e
E g Silicio = 1.1 eV
funzione di lavoro del silicio
qφSilicio
qφM Au ≅ 4.75 eV ,
la barriera è nominalmente di 0.6 eV mentre la
dipende dal livello di drogaggio.
In realtà questa relazione si realizza raramente ed i valori sperimentali misurati a volte differiscono
fortemente per diversi motivi tra cui:
•
Per la presenza di uno strato di isolante all’interfaccia
•
Presenza di trappole di superficie
•
Stati di energia nella banda proibita di energia del semiconduttore dovuti alla diffusione di
atomi di metallo
•
Dipoli di interfaccia
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-4
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-5
La figura inoltre mostra la differenza nella giunzione tra quando si metallizza un semiconduttore ptype ed uno n-type.
Come nella giunzione p-n si forma dunque una regione di carica spaziale che si estende solo nel
semiconduttore.
In polarizzazione inversa ( Va < 0 V) l’estensione di questa regione è:
W=
2ε s (Vbi − Va )
qN semicond
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-6
L’integrale del campo dà la tensione di built in.
Vbi = −
1
1 ND 2
ε
W
=
q
W
max
2
2 εs
Dalla figura si vede anche che
⎛
E − EF ⎞
Vbi = φM − φs = φM − ⎜ χ + C
⎟
q
⎝
⎠
dalla capacità corrispondente è possibile ricavare come per la giunzione p-n il drogaggio del
semiconduttore e il potenziale di built-in.
(Vbi − Va )
1
=
2
Cd2
qε s N semicond .
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-7
La carica spaziale per unità di area nel semiconduttore è:
Qs = qN DW = 2qε s N DVbi
Come per la giunzione p-n, se applico un segnale variabile nel tempo ho un comportamento
capacitivo, dove la capacità per unità di area è:
C=
∂Qs
qε s N D
ε
=
= s
∂Va
2 (Vbi − Va ) W
La corrente che circola può essere di diversa origine:
•
Corrente termoionica: è una corrente di portatori maggioritari che hanno energia sufficiente
(grazie anche alla temperatura) per scavalcare la barriera di potenziale. L’espressione di questa
corrente è:
*
2
J term = A T e
−
qφ B
kT
" qV f
%
$ e ηkT −1'
$
'
#
&
dove
A* =
4π qm*k 2
h3
è chiamata costante di Richardson e dipende dal semiconduttore e dal suo drogaggio
•
A*
Si
GaAs
Ge
n-type
110
4.4
143
p-type
30
74
41
Corrente di tunnelling: a differenza di quella vista nella rottura Zener, in questo caso il
portatore attraversa la regione di carica spaziale per passare dal metallo alla banda
corrispondente (BC per gli elettroni e BV per le lacune) o viceversa. L’espressione è
comunque simile e dipende esponenzialmente dalla larghezza della regione di carica spaziale.
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-8
•
Corrente di minoritari: Nel caso di una giunzione metallo-semiconduttore drogato n è la
corrente di lacune limitata dalla diffusione come nel caso della giunzione p-n ed è data da:
a
qDp pn0 ⎡ qV
⎤
kT
Jh =
⎢e − 1⎥
Lp ⎣
⎦
ed è circa 4-6 volte inferiore alla corrente termoionica. Quindi la corrente dominante è quella
dei maggioritari. Ciò fa sì che il diodo Schottky, costituito da un semiconduttore con un
contatto Schottky e l’altro ohmico abbia velocità di oltre due ordini di grandezza superiori
rispetto al diodo p-n (100GHz contro 1 GHz)
•
Corrente di generazione/ricombinazione: è la stessa corrente che si sviluppa in regione di
carica spaziale già vista per la giunzione p-n ed è più importante per basse tensioni di
polarizzazione.
Jg/r
⎡ 2qVkTa ⎤
= J re ⎢e − 1⎥
⎣
⎦
dove J re dipende dalla qualità del materiale.
La caratteristica completa I-V della giunzione è
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-9
Metodi di misura della barriera di potenziale φB
Esistono 5 metodi principali per la misura dell’altezza della barriera.
•
Caratteristica I-V: se il meccanismo di corrente che circola alla giunzione M-S è
principalmente quello della corrente termoionica, conoscendo A*, è possibile estrapolare
φB
•
dalla relazione
J term = A T e
*
2
−
qφB
kT
⎛ − qV f
⎞
η kT
⎜e
− 1⎟
⎜
⎟
⎝
⎠
Dipendenza dalla temperatura di della corrente in polarizzazione diretta J F : di nuovo uso
l’espressione della corrente termoionica e fissata una polarizzazione VF , misuro J F in
funzione della temperatura. Rappresento graficamente log(
JF
1
) vs ed ottengo una curva
2
T
T
la cui pendenza mi dà un’energia di attivazione proporzionale a q(φB − VF )
•
Metodo C-V: è il metodo già visto. Calcolo Vbi e qVn (distanza di E F da EC ) La somma
dei due mi dà qφB
•
Metodo della fotocorrente: Eccito la giunzione con una sorgente ottica monocromatica di
energia variabile. L’efficienza quantica per portatori fotoeccitati dal metallo sopra la
barriera è una funzione dell’energia del fotone hν . Se si rappresenta graficamente la radice
quadrata della fotocorrente in funzione di hν si ottiene dall’intercetta con l’asse x l’altezza
della barriera
•
Effetto fotovoltaico: quando una barriera Schottky è esposta alla luce, è possibile misurare
una corrente di cortocircuito J cc o una tensione di circuito aperto Vca .
La relazione che lega queste due quantità è
Vca =
nkT ⎛ J cc ⎞
ln ⎜
+ 1⎟
q
J
⎝ 0
⎠
dove J 0 è la corrente di buio. Dalla misura di J cc e Vca a diverse intensità della luce,
ottengo J 0 e n da cui calcolo qφB .
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-10
Effetto forza immagine
In un’approssimazione del primo ordine l’ampiezza della barriera di potenziale, qΦB, che si
oppone al flusso di elettroni dal metallo verso il semiconduttore è indipendente dalla tensione
applicata alla giunzione. Questa assunzione però non è corretta: in realtà, un fenomeno noto come
“image-force lowering” riduce l’altezza della barriera di potenziale rispetto al caso ideale, rendendola
dipendente dal potenziale applicato.
Se pongo un elettrone ad una distanza x da un piano metallico infinitamente esteso, esso viene
attratto verso la superficie metallica da una forza coulombiana pari a:
F=
− q2
4πε 0 ⋅ (2x ) 2
dove ε0 indica la permittività del vuoto e q la carica elettronica.
Ho cioè la situazione analoga al porre due cariche di tipo opposto ad una distanza doppia 2x.
La sua energia, considerata nulla ad una distanza infinita dal piano, risulta pari a:
x
E ( x ) = ∫ Fdx =
∞
x
La E ( x ) = ∫ Fdx =
∞
− q2
16 πε 0 x
− q2
indica che la barriera di potenziale all’interfaccia con il metallo non ha un
16 πε 0 x
profilo spigoloso (come nell’ipotesi ideale), bensì più arrotondato, come appare nella rappresentazione
a bande di energia nella figura seguente
Quando l’elettrone risente della presenza di un campo elettrico esterno
ε
x
(come quello dovuto alla
presenza della regione di carica spaziale della giunzione), l’espressione caratteristica della sua energia
viene modificata, diventando:
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-11
⎡ q2
⎤
E ( x) = − ⎢
+ q ⋅ε x ⋅ x⎥
⎣16πε 0 x
⎦
Di conseguenza anche la struttura a bande viene modificata:
La presenza di un campo elettrico esterno quindi abbassa l’altezza della barriera di potenziale di una
quantità:
ΔΦ B =
Dove
ε
m
=
2qN D (Vbi − Va )
εs
qε m
4πε s
è il campo elettrico massimo all’interfaccia
Quindi la giunzione reale avrà un diagramma a bande del tipo
Questi risultati restano validi anche quando riferiti ad una giunzione metallo-semiconduttore, purché
siano chiare le seguenti considerazioni:
1. la permittività del semiconduttore εs deve sostituirsi a quella del vuoto ε0;
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-12
2. il trasferimento di elettroni dal semiconduttore al metallo fino al raggiungimento
dell’equilibrio termodinamico ridistribuisce la carica in prossimità della giunzione
instaurando un campo elettrico permanente che fa sì che il fenomeno di “image-force
lowering” sia verificato anche in condizione di equilibrio (in assenza di polarizzazione);
3. l’applicazione di un campo elettrico esterno equivale a considerare l’applicazione di una
polarizzazione Va alla giunzione metallo-semiconduttore.
Ulteriori effetti secondari, quali la presenza di trappole superficiali, strati isolanti all’interfaccia
metallo-semiconduttore, stati energetici permessi all’interno del band-gap indotti dal metallo,
modificano ulteriormente l’espressione ideale della barriera qΦB.
E’ possibile volontariamente realizzare un aumento della barriera mediante il drogaggio
Il contatto Ohmico
E’ un caso speciale di giunzione Schottky.
La resistenza di interfaccia è molto piccola e si ottiene una caratteristica non rettificante ma
simmetrica e praticamente lineare.
I principali meccanismo sono illustrati in figura:
•
TE: Thermoionic emission (emissione termoionica)
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-13
•
FE: Field emission (tunnelling)
•
TFE: Thermoionic field emission (emissione termoionica + tunnelling)
La scelta del materiale per il contatto è critica. In generale le barriere dei materiali drogati p sono più
basse e quindi su questi materiali i contatti ohmici sono più facili. Sono molto complicati invece i
contatti sui materiali ad elevata energy gap.
Non è tanto importante la linearità quanto una bassa resistenza specifica di contatto:
−1
⎛ ∂J ⎞
Rc = ⎜
⎟
⎝ ∂V ⎠V →0
Poiché R =
Ω ⋅ cm2
Rc
la resistenza aumenta con la miniaturizzazione dei dispositivi.
A
La resistenza specifica di contatto dipende fortemente dal drogaggio come nel grafico seguente
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-14
La caratterizzazione della resistenza specifica di contatto è effettuata mediante la tecnica della
lunghezza di trasferimento o Trasmission Line Model (TLM). Tale tecnica prevede la realizzazione di
particolari strutture test processate sui campioni durante il processo di fabbricazione che consistono in
un pattern lineare di otto piazzole rettangolari (pad) di contatto ohmico con un interspazio variabile ad
esempio da 4 a 25µm, come mostrato schematicamente in figura.
La resistenza totale Rij misurata tra due piazzole consecutive è legata alla resistenza di contatto Rc
espressa in ohm per unità di larghezza della piazzola (Ωmm), ed alla resistenza di strato del
semiconduttore (sheet resistance, Rsh) espressa convenzionalmente in Ω/□ (Ω per quadro), attraverso
la relazione
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-15
Rij = 2 RC + d ij
Rsh
Wc
dove dij è la lunghezza dell’interspazio tra le varie piazzole di contatto (variabile) e Wc la larghezza di
ciascuna piazzola.
Rappresentando graficamente Rij in funzione di dij si ottiene, tipicamente, una retta dalla cui pendenza
e dall’intercetta sull’asse delle ordinate si ricavano, rispettivamente, le resistenze Rsh e Rc.
Assumendo che la resistenza di strato del semiconduttore non vari durante la realizzazione del
contatto ohmico, è possibile calcolare la resistenza specifica di contatto, ρc, mediante l’equazione
ρ c = Rsh L2t
dove Lt è la lunghezza di trasferimento data da
Lt = Wc
Rc
.
Rsh
Questa tecnica non è accurata per la misura di resistenze specifiche di contatto inferiori a 10-7 Ωcm2.
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-16
Leghe tipiche di contatto
Dispositivi Elettronici – Capitolo IV: La giunzione Schottky
IV-17