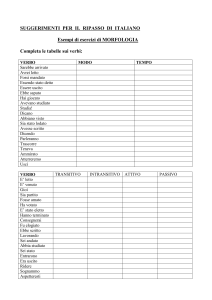
1. In quale figura la seconda lettera è simmetrica rispetto alla prima?
Figura 1
Figura 2
Figura 3
Figura 4
2. Una omotetia di rapporto 1,5 trasforma un quadrato A di area 9 cm 2 in un
quadrato B. Quale è l’area di B?
3. Estraendo due carte da un mazzo di carte napoletane (senza ributtarle nel
mazzo), quale è la probabilità che siano due figure, che almeno una sia una
figura, che sia una carta d’oro ovvero una figura?
4. In un cassetto ci sono, mescolate tra loro, 2 paia di calzini gialli, 2 paia di
calzini rossi e 2 paia di calzini verdi. Se sono al buio, qual è il numero
minimo di calzini che devo prendere per essere sicuro di avere almeno 2
calzini dello stesso colore?
1. Un disco d’oro ha il diametro di 6 cm. Un orefice propone di dividerlo in due
parti, la prima di raggio 3 cm e la seconda la corona circolare rimanente. È
una divisione equa. Se no quale delle due parti è maggiore.
2. Lanciando tre volte una moneta quale è la probabilità che vengano tutti e tre
testa, almeno una testa, una testa e due croci?
3. Due trapezi sono simili. Il primo ha lato 4 cm e area 12 cm 2; il secondo ha
lato 3 cm. Quale è l’area del secondo?
4. Mettere in ordine crescente i seguenti numeri
3/100; 0,125; 1/3; 0,65;
1. La superficie di un cubo di legno è stata completamente verniciata.
Il cubo viene poi segato lungo le linee tratteggiate. Si ottengono
così diversi cubetti, dei quali alcuni non hanno nessuna faccia
verniciata, altri una o più facce verniciate.
Indicare quanti dei cubetti hanno 0, 1, 2, 3, 4, 5, o 6 facce
verniciate.
2. Due prismi sono simili. Il primo ha lato di base 8 cm e area 180 cm 3; il
secondo ha lato 4 cm. Quale è il volume del secondo?
3. Lanciando due dadi quale è la probabilità che entrambe le facce
presentino un tre, quale la probabilità che almeno una presenti un tre e
quale quella che la somma faccia tre?
4. Il prezzo di una padella dipende dal suo diametro d secondo la
formula
prezzo = (1/15)d2 Dire se questa è una legge di proporzionalità
diretta o inversa e tracciarne il grafico.
1. 2,5,3,5 Se i due quadrati ABCD e A’B’C’D’ sono uguali quale è il rapporto tra
l’area della figura colorata in blu del primo e quella di quella colorata in rosso
della seconda?
2. Un dado non truccato è stato lanciato 70 volte;
l’uno è uscito 11 volte
Il due è uscito 10 volte
Il tre è uscito 11 volte
Il quattro è uscito 16 volte
Il cinque è uscito 9 volte
Il sei è uscito 13 volte
Dire quali di queste affermazioni sono vere:
a. Poiché il 5 è uscito meno volte la probabilità che nel prossimo lancio esca
il 5 è maggiore rispetto agli altri numeri
b. Poiché il 4 è uscito più volte la probabilità che nel prossimo lancio esca il
4 è maggiore rispetto agli altri numeri
c. La probabilità che esca il 4 o il 5 è uguale.
3. Prendiamo un numero n e consideriamo il prodotto n(n-1). Questo
numero è:
a. Sempre pari.
b. Sempre dispari.
c. Dipende da n
Motivare la risposta.
4. Si dispone di un trapezio isoscele che ha base minore di 5 cm. Se ne
vogliono usare due per costruire un esagono regolare di lato 5 cm. Quanto
devono misurare i suoi angoli perché l’operazione sia possibile? Quanto
devono misurare i lati obliqui e la base maggiore?
….
1. Questa è una successione di triangoli equilateri costruiti a partire dal
primo usando più copie di questo. Ci sarà un elemento di questa
successione formato da 300 triangoli? E da 144? Motivare la risposta.
2. La probabilità che domani piova è del 60%, che piova dopodomani del 30%.
Quale è la probabilità che piova in almeno uno dei due giorni?
3. Due rombi sono simili. Il primo ha lato 4 cm e area 12 cm 2; il secondo ha area di
24 cm2. Quale è il lato del secondo?
4.
Questo grafico rappresenta il profilo di una tappa del giro d’Italia. Stabilire quali
di queste affermazioni è vera:
a. La tappa è lunga 125 km
b. L’altitudine massima raggiunta è di 1844 m
c. Il dislivello tra Bolzano e l’arrivo è di 2110 m
d. La distanza tra Bolzano e l’arrivo è di 33,6 km