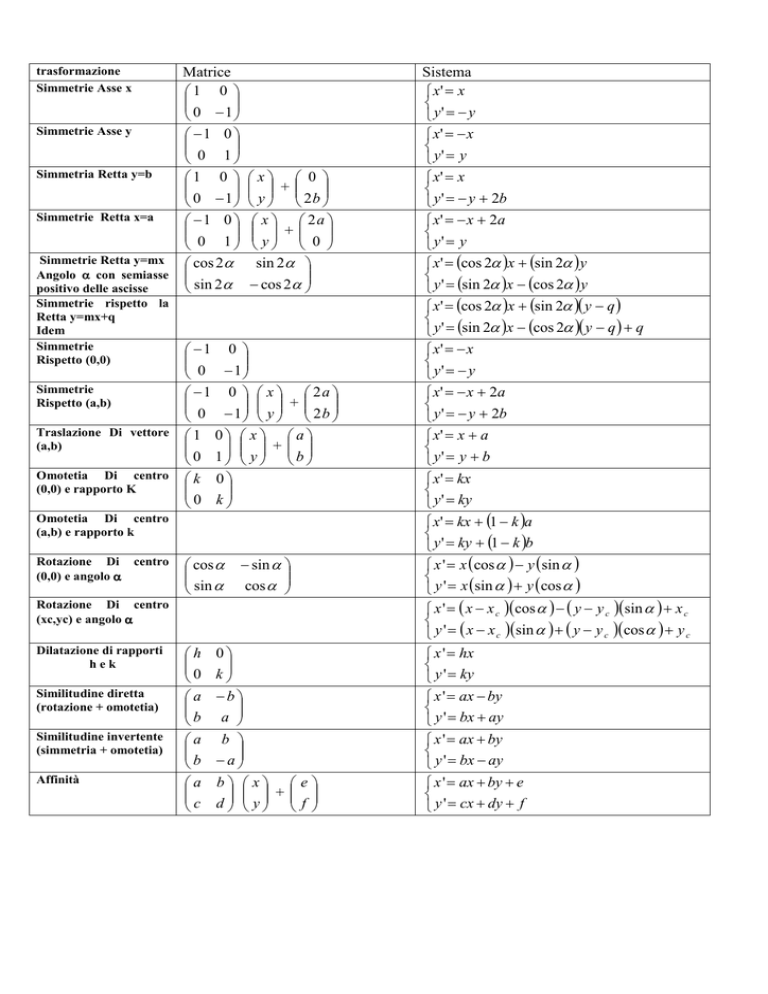
trasformazione
Simmetrie Asse x
Matrice
1 0
0 −1
Sistema
x' = x
y' = − y
Simmetrie Asse y
−1 0
0 1
1 0
0 −1
x' = − x
y' = y
x' = x
y ' = − y + 2b
Simmetria Retta y=b
Simmetrie Retta x=a
Simmetrie Retta y=mx
Angolo α con semiasse
positivo delle ascisse
Simmetrie rispetto la
Retta y=mx+q
Idem
Simmetrie
Rispetto (0,0)
Simmetrie
Rispetto (a,b)
Traslazione Di vettore
(a,b)
Omotetia Di centro
(0,0) e rapporto K
x 0
+
y 2b
x 2a
+
y 0
−1 0
0 1
cos 2α sin 2α
sin 2α − cos 2α
−1 0
0 −1
−1 0 x 2a
+
0 − 1 y 2b
1 0 x a
+
0 1 y b
k 0
0 k
Omotetia Di centro
(a,b) e rapporto k
Rotazione Di centro
(0,0) e angolo α
cos α
sin α
− sin α
cos α
Rotazione Di centro
(xc,yc) e angolo α
Dilatazione di rapporti
hek
Similitudine diretta
(rotazione + omotetia)
Similitudine invertente
(simmetria + omotetia)
Affinità
h 0
0 k
a −b
b a
a b
b −a
a b
c d
x e
+
y f
x ' = − x + 2a
y' = y
x' = (cos 2α )x + (sin 2α ) y
y ' = (sin 2α )x − (cos 2α ) y
x' = (cos 2α )x + (sin 2α )( y − q )
y ' = (sin 2α )x − (cos 2α )( y − q ) + q
x' = − x
y' = − y
x ' = − x + 2a
y ' = − y + 2b
x' = x + a
y' = y + b
x' = kx
y ' = ky
x' = kx + (1 − k )a
y ' = ky + (1 − k )b
x ' = x ( cos α ) − y ( sin α )
y ' = x (sin α ) + y ( cos α )
x ' = ( x − x c )( cos α ) − ( y − y c )( sin α ) + x c
y ' = ( x − x c )(sin α ) + ( y − y c )( cos α ) + y c
x ' = hx
y ' = ky
x ' = ax − by
y ' = bx + ay
x ' = ax + by
y ' = bx − ay
x ' = ax + by + e
y ' = cx + dy + f












