Esercizi su semiconduttori e diodi

Università degli Studi di Roma Tor Vergata
Dipartimento di Ing. Elettronica
corso di
ELETTRONICA APPLICATA
Ing. Rocco Giofrè
Esercizi su semiconduttori e
diodi
ESERCIZIO - GIUNZIONE P-N POLARIZZATA
Una giunzione pn, a cui è applicata una polarizzazione diretta, conduce
una corrente I=2.2µA. La giunzione ha una concentrazione di accettori
NA=1016cm-3 e una concentrazione di donori ND=1015cm-3 e un’area
A=400µm2. Nelle due zone si può assumere, alla temperatura di 20°C,
µp=480 [cm2 V-1 s-1 ], µn=1350 [cm2 V-1 s-1 ], τp =20*10-9 [s], τn =45*10-9 [s],
ni =1010 [cm-3 ].
a) Si trovi la tensione di polarizzazione VA che produce la corrente
specificata e la corrispondente tensione di barriera.
b) Si calcolino le cariche in eccesso immagazzinate nelle zone p ed n e
la carica complessiva.
c) Si determini la capacità di diffusione nelle condizioni specificate.
Si ricorda che la corrente di saturazione
inversa in un diodo è data dalla:
A cura dell’Ing. R. Giofrè
⎛ DP
Dn ⎞
⎟⎟
+
I S = Aqni2 • ⎜⎜
⎝ N D LP N A Ln ⎠
PUNTO A
La corrente che circolante in un diodo è data
(come è noto!) dalla formula:
⎛ VVA ⎞
I = I s • ⎜ e T − 1⎟
⎜
⎟
⎝
⎠
⎛I
⎞
VA = VT • ln⎜⎜ + 1⎟⎟ Dove: VT = KT = 25.23 mV
q
⎝ Is ⎠
Per risolvere l’equazione di cui sopra è necessario prima determinare la
corrente di saturazione inversa:
⎛ DP
Dn ⎞
⎟⎟
I S = Aqni2 • ⎜⎜
+
⎝ N D LP N A Ln ⎠
È necessario determinare
D P D n e L P Ln
Per determinare DP e Dn si può ricorrere alle relazioni di Einstein:
DP
µP
= VT =
A cura dell’Ing. R. Giofrè
Dn
µn
Dn = VT • µ n = 34,08 cm 2 / s
DP = VT • µ P = 12,12 cm 2 / s
Attenzione alle
unità di misura
PUNTO A
Per determinare LP e Ln si può ricorrere alle relazioni di Einstein:
LP = DPτ P = 12,12 • 20 • 10 −9 = 492,3 • 10 −6 cm = 4,923µm
Ln = Dnτ n = 34,08 • 45 • 10 −9 = 1238,4 • 10 −6 cm = 12,38µm
Noto il valore di tali grandezze e ricordando il valore della superficie della
giunzione A=400µm2 e il valore della concentrazione intrinseca ni=10cm-3
⎛ DP
Dn ⎞
⎟⎟ = 1,98 • 10 −15 A
+
I S = Aqn • ⎜⎜
⎝ N D LP N A Ln ⎠
2
i
Attenzione alle
unità di misura
NOTA: L’effettiva corrente che si ha nel diodo con polarizzazione inversa è
molti ordini di grandezza maggiore del valore teorico dato
dall’equazione usata. A tale corrente teorica si sommano infatti
diversi fattori non previsti dal semplice modello assunto per la
giunzione, ma soprattutto gli effetti delle correnti che si generano
nelle zone di confine, dove la giunzione raggiunge la superficie del
semiconduttore.
A cura dell’Ing. R. Giofrè
PUNTO A
Si può quindi calcolare la tensione di polarizzazione esterna che dà la
corrente I = 2.2 µA (si noti che I è 1.1*109 volte la corrente di saturazione Is)
−6
⎛I
⎞
⎛
⎞
2
,
2
10
•
−3
+ 1⎟⎟ = 525,83 mV
VA = VT • ln⎜⎜ + 1⎟⎟ = 25,25 • 10 • ln⎜⎜
−15
⎝ 1,98 • 10
⎠
⎝ Is ⎠
La tensione di barriera è data da Vj =V0 –VA. Il valore di V0 all’equilibrio
(senza polarizzazione) si ricava dalla seguente espressione:
⎛ N AND ⎞
⎟⎟ = 640 mV
V0 = VT • ln⎜⎜
2
⎝ ni ⎠
e quindi, nelle condizioni considerate, la tensione di barriera Vj è
V j = V0 − VA = 0,640 − 0,52 = 114,17 mV
A cura dell’Ing. R. Giofrè
PUNTO B
L’espressione della carica Qp in eccesso nella zona neutra N e
analogamente la carica Qn in eccesso nella zona neutra P (fuori della zona
di svuotamento o regione di carica spaziale) sono le seguenti:
(slide 25 e 15)
⎛ VVA ⎞
Q p = AqL p pn 0 ⎜ e T − 1⎟ = I p • τ p
⎜
⎟
⎝
⎠
⎛ VVA ⎞
Qn = AqLn n p 0 ⎜ e T − 1⎟ = I n • τ n
⎜
⎟
⎝
⎠
L’espressione della corrente di lacune nella zona N e analogamente la
corrente di elettroni nella zona P si desume dalle equazioni di continuità
(slide 25 e 15): :
I p = A• J
diff
p
⎛ VVA ⎞
Dp
= Aq
pn 0 ⎜ e T − 1⎟
⎜
⎟
Lp
⎝
⎠
I n = A • J ndiff
⎛ VVA ⎞
Dn
= Aq
n p 0 ⎜ e T − 1⎟
⎜
⎟
Ln
⎝
⎠
Con i dati specificati si ha:
( )
2
ni2
1010
5
−3
pn 0 =
=
=
10
cm
ND
1015
A cura dell’Ing. R. Giofrè
( )
2
n p0
ni2
1010
4
−3
=
=
=
10
cm
NA
1016
PUNTO B
Dai valori determinati è ora possibile calcolare le due correnti:
I p = A • J pdiff
I n = A • J ndiff
⎛ VVA ⎞
pn 0 ⎜ e T − 1⎟ = 2 µA
= Aq
⎜
⎟
Lp
⎝
⎠
Dp
VA
⎛
⎞
Dn
V
T
= Aq
n p 0 ⎜ e − 1⎟ = 0,2 µA
⎜
⎟
Ln
⎝
⎠
come si vede, si ha corrente maggiore nella zona N, che è la meno drogata.
E’ utile verificare che la somma delle due correnti dà la corrente totale
specificata, cioè Ip +In = I =2.2 µA.
Infine, dai valori delle correnti e tenendo conto che τp =20*10-9 s e τn =45*10-9
s, si ottiene:
Q p = I p • τ p = 40 • 10
−15
C
Qn = I n • τ n = 8,9 • 10 −15 C
QTot = Q p + Qn = 48,9 • 10 −15 C
A cura dell’Ing. R. Giofrè
PUNTO C
La capacità di diffusione è data da:
τT I T
CD =
ηVT
Dove:
•
•
•
•
I = è la corrente totale calcolata in precedenza
τT = è il tempo di vita medio totale delle cariche
η = è il fattore di idealità
VT = è l’equivalente in tensione della temperatura
VT =
Come calcoliamo il tempo di vita totale delle cariche???
kT
≅ 25 mV
q
rappresenta la media pesata tra i tempi di vita medi degli elettroni e delle lacune
Qual’è la grandezza che
è direttamente legata ai
tempi di vita medi??
Corrente o carica!
τT =
τp I p + τ n I n
e quindi per una corrente IT=2.2µA e una tensione VA=0.52V
CD =
τI
= 1.98 pF
ηVT
A cura dell’Ing. R. Giofrè
IT
= 22.7 ns
ESERCIZIO SUI DIODI (Metodo degli Scatti)
Determinare la transcaratteristica vout(vin) del seguente
circuito
R
Vout
Vin
Dati del problema
• VR = 5V
• Ro = 1 k Ω
• R = 10 Ω
• VZ = -8V
•V٧ = 0.7V
•rD = 0 Ω
•rZ = 0 Ω
•ri = ∞ Ω
DZ
D
Ro
VR
Metodo degli scatti
Si determinano i punti di scatto di ogni diodo nel circuito imponendo la condizione id=0A
e vd=v٧ ( nel caso ideale id=0A e vd=0V ). Nel piano della curva di trasferimento
v0=f(vi) si riportano i punti di scatto così individuati e si uniscono con tratti di retta. I lati
estremi della caratteristica linearizzata si determinano calcolando la pendenza delle
semirette, con origine nei punti di scatto estremi, per vi<<0 e vi>>0 .
A cura dell’Ing. R. Giofrè
Circuito equivalente di un diodo zener
+
_
+ VAB
VA
_
Vγ
VB
IDZ
VAB
IDZ
VA
VB
|VZ|
Il circuito equivalente del diodo Zener si ottiene in tre semplici passaggi:
1.
2.
3.
Due diodi ideali antiparalleli
Un generatore di tensione |V٧| in serie al diodo che ha la punta nello
stesso verso del diodo zener e con il polo positivo verso il polo negativo
del diodo (regione n)
Un generatore di tensione |Vz| in serie al diodo che ha la punta nel verso
opposto del diodo zener e con il polo negativo verso il polo positivo del diodo
(regione p) (praticamente il ramo superiore invertito)
Perchè?
1.
2.
Lo zener conduce come un diodo "normale" quando VAB>V٧ (ramo sup.)
Si comporta come un diodo nel verso opposto quando VAB<-|VZ| (ramo inf.)
A cura dell’Ing. R. Giofrè
Circuito equivalente di un diodo zener II
VA
VAB
+
_
+ VAB
_
Vγ
VB
IDZ
VA
IDZ
VB
|VZ|
Nella regione 3 e quindi per VAB> V٧ lo zener si
comporta come una batteria di valore V٧
IDZ
Nella regione 2 e quindi per VAB< -|VZ| lo zener
si comporta come una batteria di valore -|VZ|
per VAB<-|VZ|
Nella regione 1 e quindi per |VZ |-< VAB < |V ٧| lo
zener si comporta come una resistenza di
valore infinito
-|VZ|
-VAB
V٧
VAB
2
1
A cura dell’Ing. R. Giofrè
-IDZ
3
ESERCIZIO SUI DIODI (Metodo degli Scatti)
Quindi Il circuito diventa:
Attenzione in questo caso la
Vz è da intendersi negativa
+
Vin
IDZ
_
VDZ
R
Vout
Vγ
VZ
Dal circuito si evince che Vout=Iout*Ro
D
ID
Ro
Iout
VR
Individuazione dei punti di scatto dei diodi
1. Sul diodo di uscita se Vout=VR+V٧ e ID=0 A
(S1)
2. Sul diodo zener Vin-Vout=V٧ e IDZ=0 A (la corrente in R è uguale a zero) (S2)
3. Sul diodo zener Vin-Vout=VZ e IDZ=0 A (la corrente in R è uguale a zero) (S3)
attenzione: la condizione di "SCATTO" è la SIMULTANEA "VD=V٧ e ID=0 A"
vout
Rappresentazione dei punti di
scatto dei diodi nel piano (Vin, Vout)
A cura dell’Ing. R. Giofrè
vin-S3
vin-S2
vin-S1
vin
ESERCIZIO SUI DIODI (Metodo degli Scatti)
Per Vin>>0 entrambi i diodi sono in conduzione diretta è Vout=VR+V٧
+
Vin
VDZ
IDZ
Vout = ( v R + v γ )
_
R
Vγ
VZ
ID
D
vout
Vout
vout-S1
Ro
Iout
VR
perchè ID=0 A
valida fino a quando Vin> Vin-S1
vin-S1
come calcolo Vin-S1???
Al punto di scatto si ha ID=0A e quindi si può scrivere:
vin − v γ − RI out − R 0 I out = 0
I out =
R0
v in − v γ ) = vR + v γ = vout − S1 = 5 + 0.7 = 5.7 V
(
R + R0
⎛
R0 ⎞
R0
vin = VR + Vγ ⎜ 1+
= vin − S1 = 6.45 V
⎟
R
R
R
R
+
+
0 ⎠
0
⎝
vout = R 0 I out =
A cura dell’Ing. R. Giofrè
vin − v γ
R + R0
vin
ESERCIZIO SUI DIODI (Metodo degli Scatti)
S2: (cioè per Vin=V٧) il diodo zener scatta in pol. dir. mentre il diodo di uscita è interdetto
VDZ
+
Vin
_
vout
R
IDZ
Vout
Vγ
VZ
ID
vin = v γ
D
Ro
Iout
VR
R0
R + R0
I DZ = 0A = I out
Vout = 0 V
vout-S1
vin-S2
vout − S 2 = 0 V
vin-S1
v in − S 2 = v γ
per Vin-S2<Vin<Vin-S1 il diodo zener è in conduzione diretta mentre il
diodo di uscita è interdetto
vin − v γ
I out =
vin − v γ − RI out − R 0 I out = 0
R + R0
Vout = R 0 I out =
A cura dell’Ing. R. Giofrè
R0
vin − v γ )
(
R + R0
Dalla quale si può determinare la
pendenza della retta!
vin
ESERCIZIO SUI DIODI (Metodo degli Scatti)
S3: (cioè per Vin=VZ ) il diodo zener scatta in pol. inv. mentre il diodo di uscita è
interdetto
_
VDZ
vout
+
Vin
IDZ
R
Vout
Vγ
VZ
ID
vin = VZ
D
Ro
vout-S1
Iout
VR
I DZ = 0A = I out
vout − S 3 = 0 V
vin-S3
vin-S2
vin-S1
vin
vin − S 3 = VZ
per Vin-S3<Vin<Vin-S2 tutte e due i diodi sono interdetti IDZ=0A
vin − v DZ − RI out − R 0 I out = 0
Vout = R 0 I out = 0 V
A cura dell’Ing. R. Giofrè
VZ<VDZ<V٧
I=
vin − vDZ
= 0A
R + R0
IZ
vZ
v٧
VZ
ESERCIZIO SUI DIODI (Metodo degli Scatti)
Per Vin<<0 lo zener è in conduzione inversa (la tensione ai suoi capi è VZ=8V), e il diodo in uscita è interdetto
vout
+
Vin
IDZ
VDZ
_
R
Vout
Vγ
VZ
ID
D
Ro
vin-S3
vin
Iout
R0
R + R0
VR
vin − v Z − RI out − R 0 I out = 0
I out =
vout-S3
Transcaratteristica globale
vout
vin − v Z
R + R0
vout-S1
R0
R + R0
vin-S3
Vout = R 0 I out =
A cura dell’Ing. R. Giofrè
R0
( vin − vZ )
R + R0
vin-S2
R0
R + R0
vin-S1
vin
Sollecitazione al circuito
Disegnare l’andamento della tensione d’uscita quando in
ingresso al circuito viene posta una sinusoide
vout
Vout
vout-S1
vin-S3
vin-S2
vin-S1
vin
Vin
t
A cura dell’Ing. R. Giofrè
t
ESERCIZIO SUI DIODI (Metodo degli Stati)
Dato il circuito di figura, ricavare la corrente I
•
•
•
•
•
•
•
V1 = 15V
V2 = 10V
R1 = 10 k Ω
R2 = 5 k Ω
V٧ = 0.7V
rD = 0 Ω
ri = 1MΩ
R1
V1
R2
D2
D1
I
V2
Metodo degli stati
Si assume che ogni diodo presente nel circuito sia in uno stato preciso (ON
o OFF) sostituendolo con il circuito equivalente relativo allo stato scelto. Il
circuito, reso lineare, è esaminato con le leggi di Kirchkoff verificando che
siano corrette le assunzioni iniziali e ripetendo l’analisi in caso di
assunzione non corretta (es. corrente positiva in un diodo considerato OFF)
A cura dell’Ing. R. Giofrè
ESERCIZIO SUI DIODI (Metodo degli Stati)
Ipotesi 1: D1 e D2 ON
Devo sostituire i due diodi con due batterie di valore V٧
R1
I1 =
I=
v1 − v γ
R1
v γ − ( − v2 ) − v γ
R2
V1
= 1.43mA
I1
R2
V٧
V٧
I
V2
= 2mA
OK
⎧ I D 2 = I = 2mA
⎨
⎩ I D1 = I1 − I = −0.57mA
NO
L’ipotesi 1
non è corretta
Lo stato del diodo D1 non è corretto, perchè la corrente che lo attraversa
risulta negativa. Infatti avendolo supposto in polarizzazione diretta la sua
corrente non può essere negativa.
A cura dell’Ing. R. Giofrè
ESERCIZIO SUI DIODI (Metodo degli Stati)
Ipotesi 2: D1 OFF e D2 ON
Devo sostituire rispettivamente: il diodo D1 con una resistenza di
valore ri e il diodo D2 con una batteria di valore V٧
R1
VD1
V٧
R2
I
V1
I=
V2
ri
v1 + v 2 − v γ
R1 + R 2
ri è sicuramente trascurabile
perchè molto elevata
D2 ON
= 1.6mA
VD1 = V1 − R1I = 15 − 16 = −1V
L’ipotesi 2 è corretta
A cura dell’Ing. R. Giofrè
D1 OFF
OK
OK
CIRCUITO A DIODI
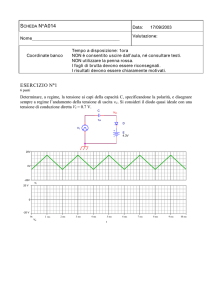
Si disegni la transcaratteristica Vo=f(VI) del circuito di figura
indicando chiaramente i punti di scatto e le pendenze dei vari tratti
giustificando la risposta. Si considerino i diodi ideali.
+
I1
Dati:
VC = 5 V
I1 = 2 mA
R1 = 1 kΩ
R2 = 2 kΩ
R3 = 2 kΩ.
R3
+
Vo
D1
+
R1
Vi
R2
Ripetere l’esercizio sostituendo il diodo D2 con un
diodo zener con VZ=-7V
A cura dell’Ing. R. Giofrè
VC
D2
CIRCUITO A DIODI
Osservando il circuito, si può supporre che, per valori sufficientemente
positivi della tensione Vin, entrambi i diodi siano interdetti. Conviene allora
iniziare l’analisi ipotizzando che:
+
D1 e D2 siano entrambi OFF
Il circuito da studiare si può semplificare come:
Vo = VC + R 3 I0 = 5 V + 4 V = 9 V
VD1 = VA − VB = VAB
Sostituendo la (1) nella (2) si ricava la condizione:
+
+
A
R1
B
Vi
Vo
R2
2
⎛
R1 ⎞
Vi > ⎜ 1+
⎟ • ( VC + R 3 I0 ) = (1.5 ) 9 = 13.5 V = Vin − D1
R
⎝
2 ⎠
A cura dell’Ing. R. Giofrè
R3
1
Questa situazione si mantiene finché la tensione
ai capi dei diodi rimane negativa. La tensione ai
capi di D2 (con le usuali convenzioni di segno) è
pari a –Vo e quindi è effettivamente negativa. La
tensione ai capi di D1 invece risulta pari a:
⎛ R2 ⎞
= Vo − Vi ⎜
⎟
R
+
R
1⎠
⎝ 2
I1
VC
Si può quindi concludere che,
per tensioni superiori a Vin-D1,
la tensione di uscita resta
fissata a 9 V.
CIRCUITO A DIODI
Per tensioni inferiori a Vin-D1, invece, il diodo D1, che è l’unico il cui stato
dipenda da Vi, si accende. Quindi il circuito diventa:
vout
D1 ON e D2 OFF
+ VC
I1
+
Vi
R3
R1 A
+
B
R2
Vo
vin-D1
vin
Per determinare la tensione di uscita conviene applicare il
principio di sovrapposizione degli effetti. Dopo qualche
passaggio, si trova:
⎛ R1 //R 2 ⎞
⎛ R 3 //R 2 ⎞
+
•
Vo = ( VC + R 3 I0 ) • ⎜
V
⎟
⎟ = 2.22 + 0.5 Vi
i ⎜
⎝ R1 //R 2 + R 3 ⎠
⎝ R 3 //R 2 + R1 ⎠
dove è possibile distinguere il contributo dei tre generatori indipendenti. Questa
situazione si mantiene finché la tensione ai capi del diodo D2 rimane negativa e la
corrente sul diodo D1 positiva.
A cura dell’Ing. R. Giofrè
CIRCUITO A DIODI
Determiniamo allora le due quantità:
+ VC
I1
+
R3
A
R1
vout
+
B
Vi
R2
Vo
vin-D1
vin
Per determinare la tensione di uscita conviene applicare il
principio di sovrapposizione degli effetti. Dopo qualche
passaggio, si trova:
⎛ R1 //R 2 ⎞
⎛ R 3 //R 2 ⎞
Vo = ( VC + R 3 I0 ) • ⎜
⎟ + Vi • ⎜
⎟ = 2.22 + 0.5 Vi
+
+
R
//R
R
R
//R
R
2
3 ⎠
2
1⎠
⎝ 1
⎝ 3
dove è possibile distinguere il contributo dei tre generatori indipendenti. Questa
situazione si mantiene finché la tensione ai capi del diodo D2 rimane negativa (ai
capi del diodo quindi finché Vo>0) e la corrente sul diodo D1 positiva.
Determiniamo allora le due quantità:
V − VC
VD 2 = − Vo
I D1 = I o − o
R3
A cura dell’Ing. R. Giofrè
CIRCUITO A DIODI
Sostituendo la (3) nella (4) e nella (5) e imponendo il segno
corretto a ciascuna quantità, si ricavano due condizioni sulla
tensione VIN. In particolare, dalla (5) si trova:
0 V = 2.22 + 0.5 Vi ⇒ Vi =
vout
−2.22
= −4.44 V = Vin − D 2
0 .5
vin-D2
vin-D1
vin
Sostituendo la (3) nella (5) otteniamo ovviamente il valore di tensione Vin-D1 quindi
questa situazione D1 ON e D2 OFF si mantiene per tensioni d’ingresso comprese
tra Vin-D2 <Vin <Vin-D1
Per Vin <Vin-D2 si nota come la tensione d’uscita resta fissa a zero volt perché il
diodo D2 entrando in conduzione cortocircuita l’uscita.
Nel caso in cui il diodo D2 fosse sostituito con
un diodo zener l’unica differenza si avrebbe
quando D2 è in polarizzazione inversa in
quanto lo zener forzerebbe il valore della
tensione d’uscita a VZ e non a Vo =VC+R3Io
cosa che si verificherà per una Vin diversa da
Vin-D1 determinata precedentemente
A cura dell’Ing. R. Giofrè
vout
vin-D2
Con D2 diodo
zener
vin-D1
vin