Potenza elettrica su carico resistivo
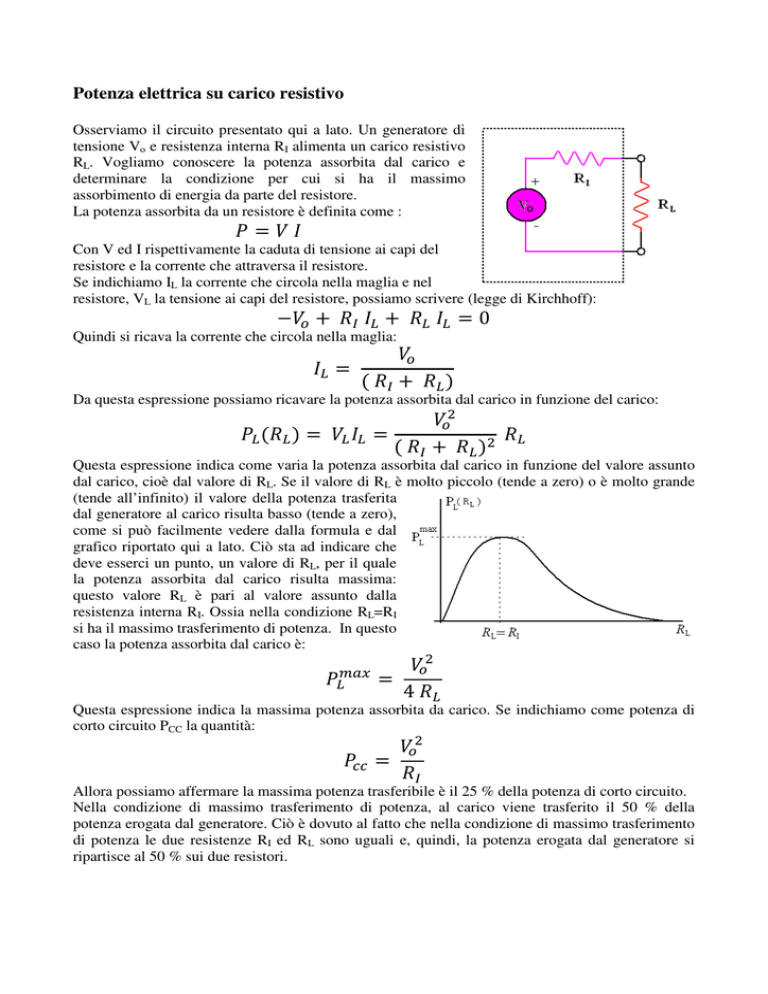
Osserviamo il circuito presentato qui a lato. Un generatore di
tensione Vo e resistenza interna RI alimenta un carico resistivo
RL. Vogliamo conoscere la potenza assorbita dal carico e
determinare la condizione per cui si ha il massimo
assorbimento di energia da parte del resistore.
La potenza assorbita da un resistore è definita come :
Con V ed I rispettivamente la caduta di tensione ai capi del
resistore e la corrente che attraversa il resistore.
Se indichiamo IL la corrente che circola nella maglia e nel
resistore, VL la tensione ai capi del resistore, possiamo scrivere (legge di Kirchhoff):
Quindi si ricava la corrente che circola nella maglia:
Da questa espressione possiamo ricavare la potenza assorbita dal carico in funzione del carico:
Questa espressione indica come varia la potenza assorbita dal carico in funzione del valore assunto
dal carico, cioè dal valore di RL. Se il valore di RL è molto piccolo (tende a zero) o è molto grande
(tende all’infinito) il valore della potenza trasferita
dal generatore al carico risulta basso (tende a zero),
come si può facilmente vedere dalla formula e dal
grafico riportato qui a lato. Ciò sta ad indicare che
deve esserci un punto, un valore di RL, per il quale
la potenza assorbita dal carico risulta massima:
questo valore RL è pari al valore assunto dalla
resistenza interna RI. Ossia nella condizione RL=RI
si ha il massimo trasferimento di potenza. In questo
caso la potenza assorbita dal carico è:
Questa espressione indica la massima potenza assorbita da carico. Se indichiamo come potenza di
corto circuito PCC la quantità:
Allora possiamo affermare la massima potenza trasferibile è il 25 % della potenza di corto circuito.
Nella condizione di massimo trasferimento di potenza, al carico viene trasferito il 50 % della
potenza erogata dal generatore. Ciò è dovuto al fatto che nella condizione di massimo trasferimento
di potenza le due resistenze RI ed RL sono uguali e, quindi, la potenza erogata dal generatore si
ripartisce al 50 % sui due resistori.
La potenza trasferita al resistore viene trasformata in calore per effetto Joule.
La potenza è legata all’energia in base alla formula:
Dove E è la quantità di energia trasferita nel tempo t. La potenza si misura in Watt mentre
l’energia si misura in Joule. Poiché l’energia è anche calore, che si misura in calorie, l’equivalenza
tra Joule (J) e Calorie (Cal) è:
Poiché deve sempre essere soddisfatto il principio di conservazione dell’energia ciò comporta che la
potenza erogata deve essere sempre uguale alla somma delle potenze utilizzate.
Un’altra unità di misura dell’energia è il Watt-Ora indicato con Wh o un suo multiplo il KWh (*).
Infatti possiamo scrivere:
% & ! $ %&
!" #
!$
!&'%&
%&
%&
Dall’ultima espressione scritta si comprende che il Wh (leggi wattora) è un’unità di misura
dell’energia e che, quindi, rappresenta la quantità di energia assorbita/fornita in un’ora.
Spesso si usa il chilo-wattora KWh il cui costo mediamente è di 30/100 di euro.
Se ad esempio teniamo acceso una lampada da 45 W per 3 ore al giorno, il contributo sulla bolletta
Enel sarà:
%
$ %&
( )!&
(!
(!
( )!& ' %&
%
$ %& %
$ %&
Quindi:
)!&
*+, + (
. $ /& $ 0 12+342$ / 563+ 7 / 563+
%&
______________
(*) Il singolare del termine “kilowattora” è “kilowattora”. Il suo plurale invece è “kilowattora”, ossia lo stesso. Questa parola composta, indicante le
migliaia di watt prodotte/consumate nel tempo di una sola ora, presenta cioè la stessa forma sia al singolare che al plurale. Non va declinato. Cioè non
si dice né “Kilowattore” né “kilowattori”.