ESAME DI ELETTROTECNICA DEL 12 GIUGNO 1998 (2) Calcolare

ESAME DI ELETTROTECNICA DEL 12 GIUGNO 1998
(2)
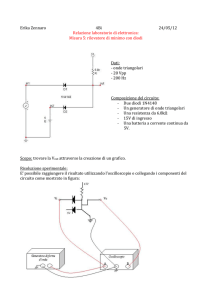
Calcolare la matrice delle impedenze di circuito aperto del doppio bipolo di figura :
1
R1
I1
I2
R2
2
I3
VR2
V1
1
α VR2
VR3 R3
1’
Z12
Z21
Z22
[Z]=
dove ogni singolo elemento è così definito:
V1
V1
Z11 =
Z12 =
I1
I2 = 0
I2
V2
I1 = 0
V2
Z21 =
Z22 =
I1
I2 = 0
I2
I1 = 0
Applichiamo ora la L.K.T. alla maglia 1 e alla 2:
1.
V1 − VR1 − VR3 = 0
VR1 = R1 I1 ;
2.
V2 + VR2 − VR3 = 0
VR2 = − R2 I2 (IR2 = -I2)
Applicando la L.K.C. al nodo A :
A.
I3 = I1 + I2
V2
2’
La matrice delle impedenze di circuito aperto è del tipo :
Z11
2
A questo punto ci serve trovare la tensione VR3 .
La corrente totale all’uscita del parallelo tra R3 ed il generatore di corrente α VR2 sarà:
I3 + α VR2
Quindi
VR3 = R3 ( I3 − α VR2 ) = R3 [ I3 − α (− R2 I2 )] = R3 [ I3 + α R2 I2 ]
A questo punto si sfrutta la L.K.C. al nodo A sostituendo I3 = I1 + I2
VR3 = R3 [ I1 + I2 + α R2 I2 ] = R3 I1 + R3 I2 (1 + α R2 )
Il sistema diventa :
V1 = R1 I1 + VR3
V2 = VR3 − VR2
⇒
⇒
V1 = R1 I1 + R3 I1 + R3 I2 (1 + α R2 )
V2 = R3 I1 + R3 I2 (1 + α R2 ) + R2 I2
V1 = (R1 + R3) I1 + R3 I2 (1 + α R2 )
V2 = R3 I1 + [R3 (1 + α R2 ) + R2 ] I2
Adesso si può scrivere la matrice delle impedenze del circuito:
V1
V1
Z11 =
= R 1 + R3
I1
Z12 =
I2 = 0
I2
V2
V2
Z21 =
= R3
I1
I2 = 0
R 1 + R3
= R3 (1 + α R2 ) + R2
Z22 =
I2
I1 = 0
R3 (1 + α R2 )
Z=
R3
= R3 (1 + α R2 )
I1 = 0
R3 (1 + α R2 ) + R2
Matrice delle
impedenze di circuito
aperto.