ESEMPI DI ANALISI DI
CIRCUITI DINAMICI LINEARI
corso: Teoria dei Circuiti
docente: Stefano PASTORE
1
Esempio di tableau ”dinamico” (tempo e Laplace)
1.1
Dominio del tempo
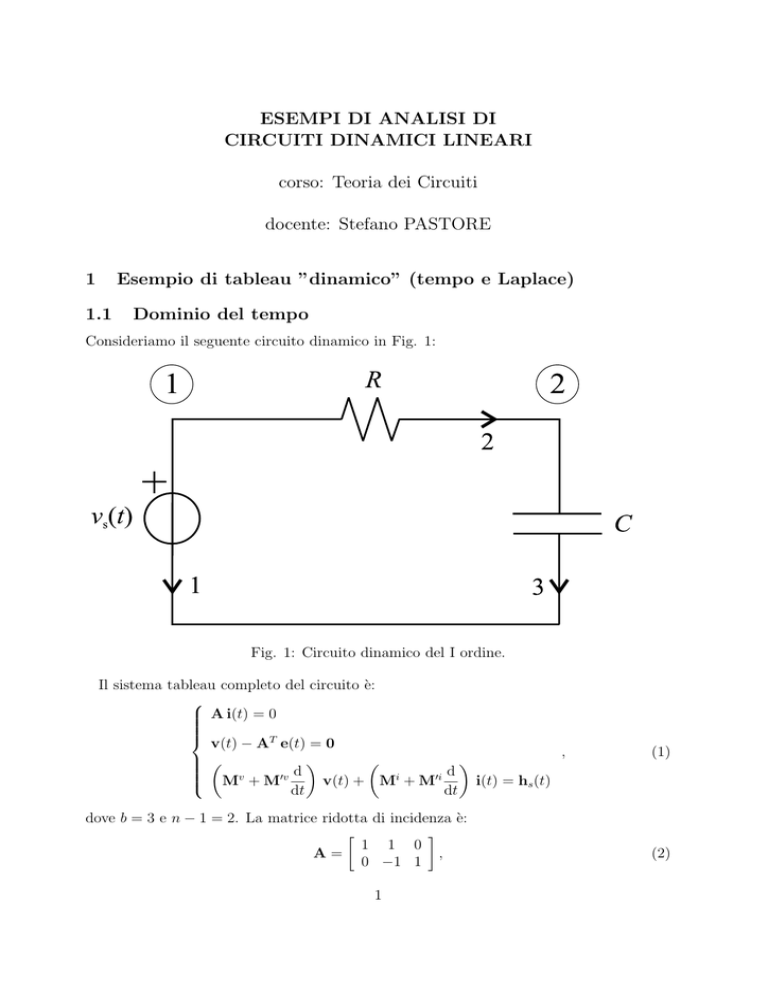
Consideriamo il seguente circuito dinamico in Fig. 1:
Fig. 1: Circuito dinamico del I ordine.
Il sistema tableau completo del circuito è:
A i(t) = 0
v(t) − AT e(t) = 0
,
d
d
v(t) + Mi + Mi
i(t) = hs (t)
Mv + Mv
dt
dt
dove b = 3 e n − 1 = 2. La matrice ridotta di incidenza è:
1 1 0
A=
,
0 −1 1
1
(1)
(2)
mentre le relazioni costitutive sono:
1 0 0
0 1 0 + d
dt
0 0 0
0 0
0
0
d
0 −R 0
0
+
+
dt
0 0 −1
0
0 0 0
v1 (t)
0 0 0 v2 (t) +
0 0 C
v3 (t)
vs (t)
0 0
i1 (t)
0 0 i2 (t) = 0 .
i3 (t)
0
0 0
(3)
Se scrivo estesamente le equazioni del tableau, ottengo un sistema con una incognita
in più rispetto al numero di equazioni. In questo esempio, l’incognita è v̇3 (t), la derivata
della tensione (variabile di stato) dell’unico elemento dinamico (condensatore). Il tableau
completo è:
e1 (t)
0
0 0 0 0 0 1 1
0
0
e2 (t)
0
0 0 0 0 0 0 −1 1
v1 (t) 0
−1 0 1 0 0 0 0 0
0
0
(t)
v
2
−1 1 0 1 0 0 0 0
0
v3 (t) = 0 .
(4)
0 −1 0 0 1 0 0 0
0
0
0
v̇3 (t)
0 1 0 0 0 0 0
0
i1 (t) vs (t)
0
0
0 0 1 0 0 0 −R 0
i2 (t)
0
0
0 0 0 0 C 0 0 −1
i3 (t)
Supponiamo che: R = 1000Ω, C = 1µF e vs (t) = 10 V. Posso allora ridurre la matrice
T direttamente con un metodo di eliminazione gaussiana delle variabili fino ad ottenere
un’unica equazione in v̇3 (t), v3 (t) e vs (t). Oppure, posso considerare la derivata v̇3 (t) un
parametro, per cui posso scrivere:
0
0 0 0 0 1
1
0
0
e1 (t)
0
0
0 0 0 0 0
−1
1
e2 (t) 0 0
−1 0 1 0 0 0
0
0
v1 (t) 0 0
−1 1 0 1 0 0
0
0
v2 (t) = 0 − 0 v̇3 (t).
(5)
0 −1 0 0 1 0
0
0 v3 (t) 0 0
0
0 1 0 0 0
0
0
i1 (t) 10 0
0
i2 (t)
0 0 1 0 0 −1000 0
0
0
i3 (t)
0
0 0 0 0 0
0
−1
0
10−6
Invertendo la matrice quadrata rimanente, si ottiene:
e1 (t)
e2 (t)
v1 (t)
v2 (t)
v3 (t)
i1 (t)
i2 (t)
i3 (t)
=
0
0 0 0 0
0
0 0 0 0
−1 0 1 0 0
−1 1 0 1 0
0 −1 0 0 1
0
0 1 0 0
0
0 0 1 0
0
0 0 0 0
1
1
0
0
−1
1
0
0
0
0
0
0
0
0
0
0
0
0
0 −1000 0
0
0
−1
2
−1
0
0
0
0
0
10
0
0
−
0
0
0
0
0
0
0
10−6
v̇3 (t) =
=
0
0
−1 0 0 1 0
0
0 1000 −1 1 0 1 −1 1000
0
0
0 0 0 1 0
0
0 −1000 0 0 0 0 1 −1000
0 1000 −1 1 1 1 −1 1000
1
1
0 0 0 0 0
1
0
−1
0 0 0 0 0
−1
0
0
0 0 0 0 0
−1
0
0
0
0
0
10
0
0
−
0
0
0
0
0
0
0
10−6
v̇3 (t) .
(6)
Pertanto, trovo la seguente equazione in v3 (t), vs (t) (= 10 V) e v̇3 (t):
10−3 v̇3 (t) + v3 (t) = 10
(7)
che, unitamente alle condizioni iniziali v3 (t) = vC (0), rappresenta la pura evoluzione
dinamica del circuito. Questa equazione viene chiamata equazione di stato del circuito,
nella variabile di stato v3 (t). La sua soluzione è:
v3 (t) = (v3 (0) − 10) e−1000 t + 10 u(t).
(8)
1.2
Dominio di Laplace
Applicando la trasformata di Laplace al circuito di Fig. 1, ottengo il seguente sistema
tableau:
A I(s) = 0
V(s) − AT E(s) = 0
,
(9)
(Mv + sMv ) V(s) + (Mi + sMi ) V(s) = Hs (s) + H0 (s)
dove H0 (s) tiene conto delle condizioni iniziali degli elementi dinamici. Nel nostro caso
particolare, si ha:
V1 (s)
1 0 0
0 0
0
0 1 0 + s 0 0
0 V2 (s) +
V3 (s)
0 0 0
0 0 10−6
0
0
0
10 s−1
0
0 0 0
I1 (s)
.
0
+ 0 −1000 0 + s 0 0 0 I2 (s) = 0 +
−6
I3 (s)
0
0
0
−1
10 v3 (0)
0 0 0
(10)
Il tableau completo T(s) è:
E1 (s)
0
0 0 0
0
1
1
0
0
0
0 0 0
0
0
−1
1
0
E2 (s)
−1 0 1 0
0
0
0
0
0
V1 (s)
−1 1 0 1
(s)
V
0
0
0
0
0
2
=
.
(11)
V3 (s)
0 −1 0 0
1
0
0
0
0
−1
0
0 1 0
0
0
0
0
I1 (s) 10 s
0
0
0 0 1
0
0 −1000 0 I2 (s)
−6
−6
0
−1
I3 (s)
10 v3 (0)
0
0 0 0 10 s 0
3
La soluzione del sistema è ottenuta invertendo la matrice T(s):
0
E1 (s)
E2 (s)
0
V1 (s)
0
V2 (s)
0
−1
= T (s)
,
V3 (s)
0
10 s−1
I1 (s)
I2 (s)
0
−6
I3 (s)
10 v3 (0)
dove la matrice T−1 (s) è:
0
0
−1
0
0
1000
1000
s
106
0
−
−
1000 + s
1000 + s
1000 + s
1000 + s
0
0
0
0
0
6
s
s
s
0 − 10
−
1000 + s
1000 + s
1000 + s
1000 + s
6
10
1000
1000
1000
0
−
1000 + s
1000 + s
1000 + s
1000 + s
1000
1
s
1
s
1
s
1
−
−
1000 + s
1000 1000 + s
1000 1000 + s
1000 1000 + s
1000
1
s
1
s
1
s
0 −
−
1000 + s
1000 1000 + s 1000 1000 + s
1000 1000 + s
s
1
s
1
s
1
s
0
−
1000 + s
1000 1000 + s 1000 1000 + s
1000 1000 + s
1
0
0
1000
1000
106
−
1000 + s
1000 + s
1000 + s
1
0
0
s
1000
106
−
1000 + s
1000 + s
1000 + s
.
6
1000
1000
10
−
1000 + s
1000 + s
1000 + s
1
s
1
s
1000
−
1000 1000 + s 1000 1000 + s
1000 + s
1
s
1
s
1000
−
−
1000 1000 + s
1000 1000 + s
1000 + s
1
s
1
s
1000
−
−
1000 1000 + s
1000 1000 + s
1000 + s
4
(12)
La tensione V3 (s) è uguale allora a:
106
1000 10
+
10−6 v3 (0) =
1000 + s s
1000 + s
10
10
v3 (0)
v3 (0) − 10 10
= −
+
+
=
+ .
1000 + s
s
1000 + s
1000 + s
s
V3 (s) =
(13)
Antitrasformando, si ottiene:
v3 (t) = (v3 (0) − 10) e−1000 t + 10 u(t)
(14)
che è la stessa espressione (ovviamente!) trovata operando nel dominio del tempo (vedi
eq. (8)).
5
2
Circuito del II ordine nel tempo (pk ∈ R)
Consideriamo il seguente circuito lineare, tempo-invariante, dinamico e autonomo, dal
momento che l’unica sorgente indipendente (di tensione) è costante (Fig. 2):
Fig. 2: Circuito dinamico del II ordine.
Notiamo che è un circuito del secondo ordine, dove le due candidate a diventare variabili
di stato, le tensioni sui condensatori, sono manifestatamente indipendenti. L’equazione
di stato del circuito dovrà assumere la forma:
ẋ(t) = Ax(t) + Bū
(15)
dove x(t) ∈ Rn , A è una matrice di dimensione [n × n], B è un vettore [n × k] e ū è un
vettore [k × 1] che rappresenta le k sorgenti del circuito. In questo caso n = 2 e k = 1,
mentre il vettore di stato è:
v1 (t)
.
(16)
x(t)=
v2 (t)
Per la scrittura dell’equazione di stato, usiamo il metodo dei ”Componenti Complementari”. A tal fine, consideriamo il doppio bipolo adinamico (resistivo) di Fig. 3.
La rappresentazione esplicita del doppio bipolo adinamico, da adottare nel caso di due
condensatori, è la rappresentazione controllata in tensione, espressa come:
g11 g21
v1
i1s
i1
=
+
(17)
i2
g12 g22
v2
i2s
Nel nostro caso, con semplici calcoli si ottiene la seguente rappresentazione:
i1
1/1500 −1/3000
−1/300
v1
=
+
i2
v2
−1/3000 1/1500
−1/300
(18)
Ricordando che le relazioni costitutive dei condensatori sono (con la convenzione nonnormale):
(19)
i1 = −C1 v̇1 , i2 = −C2 v̇2
6
Fig. 3: Doppio-bipolo adinamico associato al circuito di Fig. 2.
e sostituendo le stesse in (18), dopo aver eseguito qualche facile operazione, trovo le
equazioni di stato rappresentate dalle seguenti matrici:
4 −2000/3 1000/3
10 /3
.
(20)
A=
, B ū =
104 /3
1000/3 −2000/3
Vediamo ora di trovare la soluzione di questa equazione differenziale, con condizione
iniziale data x(0). Troviamo innanzi tutto gli autovalori e gli autovettori della matrice
A. per far ciò, si deve risolvere l’equazione:
det[sI − A] = s2 +
I due autovalori sono:
4000
3 × 106
s+
= 0.
3
9
s1 = −1000
.
s2 = −1000/3
(21)
(22)
Il primo autovettore destro deve soddisfare all’equazione:
[s1 I − A] x1 = 0,
da cui si ottiene lo spazio lineare rappresentato da:
1
x1 =
.
−1
(23)
(24)
Il secondo autovettore è ottenuto dall’equazione:
[s2 I − A] x2 = 0,
da cui si ottiene lo spazio lineare rappresentato da:
1
x2 =
.
1
7
(25)
(26)
Sapendo che:
−1
A = S Adiag S
=
1 1
−1 1
e che:
At
e
=S
−1000
0
0
−1000/3
0
e−1000 t
0
e−1000/3 t
1/2 −1/2
1/2 1/2
,
(27)
S−1 ,
si trova l’espressione dell’esponenziale della matrice A:
−1000 t
−1000 t
−e
+ e−1000/3 t /2
+ e−1000/3 t /2
e
eA t = .
−1000 t
−e−1000 t + e−1000/3 t /2
e
+ e−1000/3 t /2
(28)
(29)
Possiamo ora considerare la presenza della sorgente costante di tensione. La soluzione
particolare, o similare, o di regime, si trova facilmente considerando degli aperti i condensatori. Le tensioni che vedo alle porte del doppio-bipolo adinamico sono:
p
v1 (t)
10
p
x (t) =
=
.
(30)
v2p (t)
10
La soluzione generale è allora:
v1 (0)
v1 (t)
10
10
At
x(t) =
= e
−
+
.
v2 (t)
v2 (0)
10
10
(31)
Un altro metodo, per trovare la soluzione generale, consiste nell’esprimere il vettore di
stato come combinazione lineare pesata degli autovettori e della soluzione particolare. Si
ha quindi:
1
1
v1 (t)
10
−1000 t
−1000/3 t
= k1 e
+ k2 e
+
,
(32)
v2 (t)
−1
1
10
dove le costante k1 , k2 ∈ R dipendono dalle condizioni iniziali. Pertanto, per t = 0, si
deve risolvere il seguente sistema in k1 e k2 :
v1 (0) − v2 (0)
2
⇒
.
v1 (0) + v2 (0) − 20
v2 (0) = −k1 + k2 + 10
k2 =
2
k1 =
v1 (0) = k1 + k2 + 10
(33)
Come si vede con una veloce sostituzione, e come deve essere, la soluzione trovata è
identica alla precedente.
8
3
Circuito del II ordine nel tempo (pk ∈ C)
Consideriamo il seguente circuito lineare, tempo-invariante, dinamico e autonomo, dal
momento che le due sorgenti indipendenti sono costanti:
Fig. 4: Circuito dinamico del II ordine.
Notiamo che è un circuito del secondo ordine, dove le due candidate a diventare variabili
di stato, la tensione sul condensatore e la corrente dell’induttanza, sono manifestatamente
indipendenti. L’equazione di stato del circuito dovrà assumere la forma:
ẋ(t) = Ax(t) + Bū
(34)
dove x(t) ∈ Rn , A è una matrice di dimensione [n × n], B è un vettore [n × k] e ū è un
vettore [k × 1] che rappresenta le k sorgenti del circuito. In questo caso n = k = 2, mentre
il vettore di stato è:
i1 (t)
.
(35)
x(t)=
v2 (t)
Per la scrittura dell’equazione di stato, usiamo il metodo dei ”Componenti Complementari”. A tal fine, consideriamo il doppio bipolo adinamico (resistivo) di Fig. 5.
La rappresentazione esplicita del doppio bipolo adinamico, da adottare nel caso di un
condensatore e di un induttore, è la rappresentazione ibrida, espressa come:
h11 h21
i1
v1s
v1
=
+
(36)
i2
h12 h22
v2
i2s
Nel nostro caso, con semplici calcoli si ottiene la seguente rappresentazione:
v1
9
0.9
10
i1
=
+
i2
v2
−0.9 0.019
0.05
(37)
Ricordando che le relazioni costitutive dei condensatori sono (con la convenzione nonnormale):
(38)
v1 = −L1 i̇1 , i2 = −C2 v̇2
9
Fig. 5: Doppio-bipolo adinamico associato al circuito di Fig. 4.
e sostituendo le stesse in (37), dopo aver eseguito qualche facile operazione, trovo le
equazioni di stato rappresentate dalle seguenti matrici:
−9 −0.9
−10
A=
, B ū =
.
(39)
900 −19
−50
Vediamo ora di trovare la soluzione di questa equazione differenziale, con condizione
iniziale data x(0). Troviamo innanzi tutto gli autovalori e gli autovettori della matrice
A. per far ciò, si deve risolvere l’equazione:
det[sI − A] = s2 + 28 s + 981 = 0.
I due autovalori complessi coniugati sono:
s1 = −14 + 28j
s2 = −14 − 28j
(= s∗1 )
.
(40)
(41)
Il primo autovettore destro deve soddisfare all’equazione:
[s1 I − A] x1 = 0,
da cui si ottiene lo spazio lineare rappresentato da:
0.032 ej2.96
−0.03 + 0.0056j
.
=
x1 =
0.9995j
0.9995 ejπ/2
(42)
(43)
Il secondo autovettore è ottenuto dall’equazione:
[s2 I − A] x2 = 0,
10
(44)
da cui si ottiene lo spazio lineare coniugato rappresentato da:
0.032 e−j2.96
−0.03 − 0.0056j
=
x2 =
−0.9995j
0.9995 e−jπ/2
(= x∗1 ).
(45)
Sapendo che:
A = S Adiag S−1 =
=
0.032 ej2.96
0.032 e−j2.96
0.9995 ejπ/2 0.9995 e−jπ/2
−14 + 28j
0
0
−14 − 28j
e che:
eA t = S
−16.07 0.5e−j1.39
−16.07
e(−14+28j)t
0
(−14−28j) t
e
0
0.5ej1.39
,
(46)
S−1 ,
si trova l’espressione di eA t :
−1.03 e−14t cos(28t + 2.96) 0.032e−14t cos(28t + 1.57)
eA t =
−32.12 e−14t cos(28t + 1.57) 0.9995e−14t cos(28t + 0.18)
(47)
(48)
Come si vede, il calcolo in forma chiusa dell’esponenziale di matrice è abbastanza lungo
e laborioso in presenza di autovalori complessi e coniugati.
Possiamo ora considerare la presenza della sorgente costante di tensione. La soluzione
particolare, o similare, o di regime, si trova facilmente applicando il principio di sovrapposizione degli effetti, dopo aver aperto il condensatore e cortocircuitata l’induttanza. La
corrente che vedo alla prima porta del doppio-bipolo adinamico e la tensione alla seconda
porta sono:
p
−0.145
i1 (t)
p
=
.
(49)
x (t) =
−9.45
v2p (t)
La soluzione generale è allora:
−0.145
−0.145
i1 (0)
i1 (t)
At
= e
−
+
.
x(t) =
−9.45
−9.45
v2 (t)
v2 (0)
(50)
Un altro metodo più rapido, per trovare la soluzione generale, consiste nell’esprimere
il vettore di stato come combinazione lineare pesata degli autovettori e della soluzione
11
particolare. Si ha quindi:
i1 (t)
−0.03 + 0.0056j
= k e(−14+28j)t
+
v2 (t)
0.9995j
+k ∗ e(−14−28j) t
−0.03 − 0.0056j
= 2 × k e(−14+28j)t
= |k|e−14t
0.032 ej2.96
+
−0.9995j
1.999 cos(28t + 1.57 + ϕk )
+
0.9995ejπ/2
−9.45
0.064 cos(28t + 2.96 + ϕk )
−0.145
−9.45
+
−0.145
−0.145
−9.45
=
(51)
,
(52)
dove la costante k = kr + j ki = |k| ejϕk dipende dalle condizioni iniziali. Pertanto, per
t = 0, si deve risolvere il seguente sistema in k:
i1 (0) = 2 × {k (−0.03 + 0.0056j)} − 0.145
.
(53)
v2 (0) = 2 × {k (0.9995j)} − 9.45
Si ottiene pertanto:
i1 (0) = −0.06kr − 0.011ki − 0.145
v2 (0) = −1.999ki − 9.45
−9.45 − v2 (0)
1.999
,
⇒
−i1 (0) − 0.06ki − 0.145
kr =
0.02
ki =
da cui si ricavano il modulo e la fase della costante k.
12
(54)
4
Circuito del II ordine con Laplace
Consideriamo il seguente circuito lineare, tempo-invariante, dinamico e autonomo, dal
momento che l’unica sorgente indipendente (di tensione) è costante:
Fig. 6: Circuito dinamico del II ordine.
Trasformiamo il circuito con Laplace estraendo le condizioni iniziali dai componenti
dinamici, mettendo il valore di impedenza accanto a ogni componente (i componenti
dinamici sono considerati inizialmente scarichi) e considerando le trasformate delle forme
d’onda delle sorgenti indipendenti. Otteniamo il seguente circuito:
Fig. 7: Circuito di Fig. 6 trasformato con Laplace.
Il circuito può essere ora risolto nel dominio della trasformata di Laplace, scrivendo
13
dunque un sistema algebrico di equazioni nella variabile s. Formalmente, è come se fosse
un circuito resistivo in continua. Scriviamo, quindi, un sistema completo e indipendente di
equazioni applicando il metodo nodale puro. Notiamo che tutti i componenti sono controllati in tensione, dal momento che ogni generatore di tensione ha in serie una impedenza.
Il sistema di 3 equazioni in 3 incognite è il seguente:
V (s) − V1 (s) V (s) − 10/s V (s) − V2 (s)
+
+
=0
10
10
10
V (s) − V (s) i (0) V (s)
1
L
1
=0
+
+
,
(55)
10
s
sL1
V2 (s) − V (s) V2 (s) − vC (0)/s
=0
+
10
1/sc1
da cui si ottiene, eliminando V (s):
2 (15 + sL1 )
10 30iL (0)
+ V2 (s) [−1] =
−
V1 (s)
sL1
s
s
.
10 + sL1
1 + s10C2
iL (0)
V1 (s) −
+ V2 (s)
=
+ C2 vC (0)
10sL1
10
s
Risolvendo
V1 (s) =
V2 (s) =
(56)
il sistema di 2 equazioni in 2 incognite, troviamo che:
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
s2 + 65s + 1000
(15 + s) (1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
1000
+ . (57)
s (s2 + 65s + 1000)
30iL (0) − 10
+
s
500
Da V1 (s) si ricava la corrente IL (s) nell’induttanza scarica:
IL (s) =
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
V1 (s)
= 500
.
sL
s (s2 + 65s + 1000)
(58)
Aggiungendo le condizioni iniziali, si ottiene infine:
iL (0)
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
= 500
+
s
s (s2 + 65s + 1000)
iL (0)
+
.
s
(59)
Da V2 (s) si ricava direttamente la tensione sul condensatore carico:
IL (s) = IL (s) +
VC (s) = V2 (s) = VC (s) +
30iL (0) − 10
s
(60)
Notiamo che la tensione VC (s) è già comprensiva della tensione iniziale sul condensatore.
Notiamo inoltre che non è conveniente procedere alla somma dei termini in IL (s) e VC (s)
per ottenere un’unica frazione, dal momento che dovremo poi procedere alla scomposizione
delle funzioni stesse per l’operazione di antitrasformazione.
14
Ora possiamo antitrasformare le due funzioni complesse IL (s) e VC (s) per ottenere le
relative funzioni nel dominio del tempo iL (t) e vC (t).
Innanzi tutto, dobbiamo trovare i poli del denominatore di IL (s) e VC (s). Si ha che:
s2 + 65s + 1000 = 0 ⇒
s1 = −40
,
s2 = −25
da cui, scomponendo IL (s) e VC (s) nella somma di frazioni parziali, si ottiene:
A
B
C
iL (0)
+
+
+
IL (s) =
s + 25! s + 40"
s
s
IL (s)
.
B
C
A
30iL (0) − 10
+
+
VC (s) =
+
s
s
+
25
s
+
40
s
!
"
VC (s)
(61)
(62)
Applicando il metodo dei residui, possiamo calcolare le costanti A, B, C, A , B e C nel
modo seguente:
A =
lim sIL (s) =
s→0
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
lim 500
=
s2 + 65s + 1000
s→0
0.5 (1 − 2iL (0))
B =
lim (s + 25)IL (s) =
s → −25
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
=
lim 500
s (s + 40)
s → −25
−1.333 (1 − 2iL (0) − 25 [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
C =
lim (s + 40)IL (s) =
s → −40
1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)]
=
lim 500
s (s + 25)
s → −40
0.833 (1 − 2iL (0) − 40 [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
15
(63)
A =
lim sVC (s) =
s→0
(15 + s) (1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
lim 1000
=
s2 + 65s + 1000
s→0
15 (1 − 2iL (0))
B =
lim (s + 25)VC (s) =
s → −25
(15 + s) (1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
lim 1000
=
s (s + 40)
s → −25
26.666 (1 − 2iL (0) − 25 [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
lim (s + 40)VC (s) =
s → −40
(15 + s) (1 − 2iL (0) + s [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
lim 1000
=
s (s + 25)
s → −40
−41.666 (1 − 2iL (0) − 40 [10−2 + 10−3 vC (0) − 3 × 10−2 iL (0)])
(64)
Le rispettive funzioni nel dominio del tempo sono infine:
C =
iL (t) = (A + iL (0) + Be−25t + Ce−40t ) u(t) A
vC (t) = (A + 30iL (0) − 10 + B e−25t + C e−40t ) u(t) V
16
(65)










