Studente ........................................................................
Matricola ...........................................
Data ............................................................
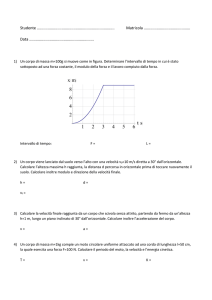
1) Un corpo di massa m=1 kg si muove come in figura. Determinare l’intervallo di tempo (tmin-tmax) in cui è
stato sottoposto ad una forza costante, il modulo della forza e il lavoro compiuto dalla forza.
vms
4
3
2
1
1
2
Intervallo di tempo:
3
4
5
6
F=
ts
L=
2) Ad un corpo di massa m=1 kg che si sta muovendo con velocità v0=10 m/s viene applicata una forza
costante con la stessa direzione della velocità, ma verso opposto. Il corpo si ferma dopo aver percorso una
distanza d=8 m. Calcolare il modulo della forza, il tempo impiegato a fermarsi, ed il lavoro fatto dalla forza.
t =
F=
L=
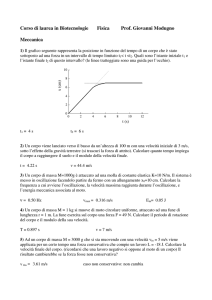
3) Calcolare la velocità massima, la forza massima e l’energia totale di un corpo di massa m=5 g che compie il
moto armonico riportato in grafico. Calcolarne inoltre la velocità a t=0.
x mm
4
2
5
10
15
20
25
30
t ms
2
4
v0 =
F=
E=
v(t=0) =
4) Un corpo viene lanciato dal suolo verso l’alto con una velocità v0=35 m/s diretta a 60° dall’orizzontale, e
successivamente ricade al suolo. Calcolare l’altezza massima h raggiunta, la distanza d percorsa in
orizzontale prima di toccare nuovamente il suolo, il modulo della velocità finale, ed il lavoro complessivo
fatto dalla forza peso.
h=
d=
vf =
L=
5) Un corpo di massa m=10 g e volume V=4 cm3 cade in acqua con una velocità costante v=1 mm/s. Calcolare
la forza di attrito viscoso, tenendo conto anche della spinta di Archimede.
Fv =
6) L’asta omogenea in figura può ruotare nel piano orizzontale (non va quindi considerata la forza peso)
intorno ad un asse verticale posto in C. Trovare il modulo della forza F2 (in funzione di F1) per il quale il
sistema è in equilibrio. Descrivere poi il moto dell’asta se l’asse si rompesse improvvisamente.
2L
F2
L
30°
C
F1
7) Se si trascurassero le forze di attrito, un corpo solido immerso in acqua affonderebbe con una
accelerazione a=4 m/s2. Calcolare la densità del corpo. Se il corpo cadesse per un intervallo di tempo di 3 s,
di quanto aumenterebbe la pressione?
=
p =
8) Considerate il tubo disegnato in figura, con r1=2 cm ed r2=0.2 cm, in cui scorre acqua. Nella sezione di
destra in un tempo t=10 s passa un volume di acqua pari a V=100 cm3, e c’è una pressione p=10000 Pa.
Trascurando la viscosità dell’aqua, calcolare la portata di volume, la velocità dell’acqua nella sezione di
sinistra e la pressione nella sezione di sinistra.
r1
Q=
v1 =
r2
p1 =
9) Si consideri di nuovo il caso dell’esercizio precedente, ma con il tubo disposto
in verticale come in figura. Spiegare sinteticamente quali delle grandezze
precedenti (Q, v, p) cambierebbero, e secondo quale legge.
10) Un’onda sonora di frequenza =5 kHz si sta propagando in aria. Calcolarne la lunghezza d’onda, e stabilire a
quale intervallo spettrale appartiene. Spiegare il motivo microscopico per il quale la velocità di
propagazione dell’onda sonora in acqua è maggiore di quella in aria.
=
intervallo spettrale:
Propagazione in acqua:
11) L’eco di un’onda sonora viene percepito dopo un’intervallo di tempo di 5 s dall’emissione dell’onda. Se
l’onda si sta propagando in aria, quale è la distanza dell’oggetto che ha provocato l’eco?
d=
12) Descrivere in modo sintetico le leggi fondamentali per velocità, accelerazione e forza nel moto circolare
uniforme.
13) Il cilindro in figura, che ha un estremo scorrevole, è riempito di aria a pressione atmosferica, ad una
temperatura T1= 60°K, e con un volume V=1 litro. Il sistema è in equilibrio con la pressione atmosferica
esterna. Se l’aria all’interno viene successivamente scaldata fino a T2=300 °C, ed il pistone scorre per
mantenere la pressione in equilibrio, qual è il nuovo volume dell’aria? Inoltre, sapendo che il volume
occupato da una mole di gas a pressione atmosferica ed a T=0°C è circa 22.4 litri, calcolare la distanza
media d tra le molecole di aria alla temperatura T1.
V=
d=
14) Discutere la definizione microscopica della temperatura assoluta di un corpo, ed un metodo ideale per
misurarla.
15) Ad un volume V=100 cm3 di acqua a T=40°C si fornisce una quantità di calore Q=1x104 cal. Calcolare la
temperatura finale dell’acqua. Se parte dell’acqua si è trasformata in vapore, calcolarne la frazione (calore
latente di evaporazione: 2250 J/g).
T=
frazione vapore/liquido =
16) Quanto vale il calore specifico di un ipotetico gas di atomi di carbonio? Basta impostare il calcolo, senza
riportarne il valore finale.
c=
17) Una sferetta di massa m1=10 g urta con velocità v1i una seconda sferetta di massa m2=5 g, inizialmente
ferma. L’urto è elastico. Calcolare la velocità delle due sferette dopo l’urto (supponendo che le velocità
siano tutte lungo la stessa direzione).
v1f =
v2f =
18) Un corpo scivola senza attrito lungo un piano inclinato di 30° dall’orizzontale. Se il corpo parte da fermo,
dopo quanto tempo si è spostato di una distanza d=15 m lungo il piano? Qual è la sua velocità finale?
t=
v=
19) Discutere in modo sintetico le leggi del moto di un corpo di massa m attaccato ad una molla di costante
elastica k, che parte dalla posizione di equilibrio con velocità v0. Definire in particolare le leggi temporali per
le grandezze: posizione, velocità, energia cinetica ed energia potenziale.