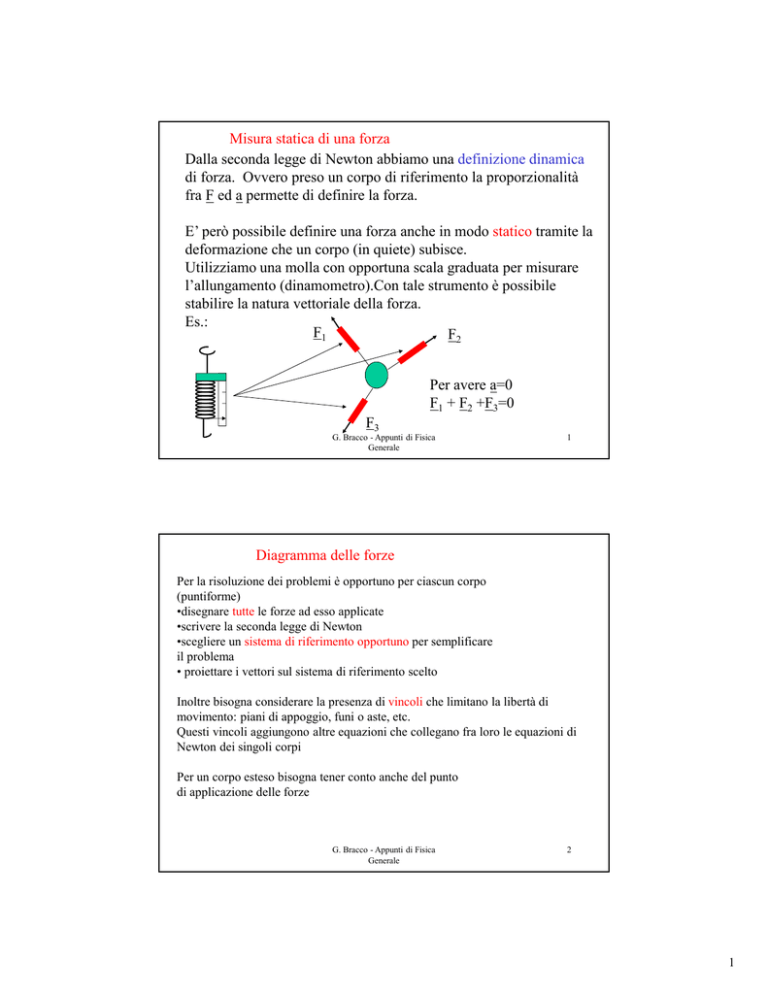
Misura statica di una forza Dalla seconda legge di Newton abbiamo

Misura statica di una forza
Dalla seconda legge di Newton abbiamo una definizione dinamica
di forza. Ovvero preso un corpo di riferimento la proporzionalità
fra F ed a permette di definire la forza.
E’ però possibile definire una forza anche in modo statico tramite la
deformazione che un corpo (in quiete) subisce.
Utilizziamo una molla con opportuna scala graduata per misurare
l’allungamento (dinamometro).Con tale strumento è possibile
stabilire la natura vettoriale della forza.
Es.:
F1
F2
Per avere a=0
F1 + F2 +F3=0
F3
G. Bracco - Appunti di Fisica
Generale
1
Diagramma delle forze
Per la risoluzione dei problemi è opportuno per ciascun corpo
(puntiforme)
•disegnare tutte le forze ad esso applicate
•scrivere la seconda legge di Newton
•scegliere un sistema di riferimento opportuno per semplificare
il problema
• proiettare i vettori sul sistema di riferimento scelto
Inoltre bisogna considerare la presenza di vincoli che limitano la libertà di
movimento: piani di appoggio, funi o aste, etc.
Questi vincoli aggiungono altre equazioni che collegano fra loro le equazioni di
Newton dei singoli corpi
Per un corpo esteso bisogna tener conto anche del punto
di applicazione delle forze
G. Bracco - Appunti di Fisica
Generale
2
1
Attrito radente
Quando due corpi sono a contatto
nascono delle forze che si oppongono
al moto relativo.
Consideriamo un corpo appoggiato su
un piano e disegniamo il diagramma
delle forze direttamente sul corpo.
Lungo la verticale c’è la forza peso
diretta verso il basso e la reazione
normale che si equilibrano. In
orizzontale applichiamo una forza F e
misuriamo il suo modulo. Dobbiamo
raggiungere un valore limite prima
che il corpo si metta in moto. Quindi
esiste una forza fS che fa equilibrio
fino al valore limite. Il valore limite è
proporzionale alla reazione normale
del vincolo N.
G. Bracco - Appunti di Fisica
Generale
3
Oltre questo valore limite una forza di
valore inferiore è necessaria a mantenere
la velocità costante. Il modulo di
questa forza è ancora proporzionale
alla reazione normale
|fS | < =|fS,max| = µS | N|
coefficiente di attrito statico µS
| fK | = µK | N |
coefficiente di attrito dinamico µK
G. Bracco - Appunti di Fisica
Generale
4
2
Forza gravitazionale
E’ la forza che agisce fra ogni coppia di corpi
mA mB
FAB= - G ---------- r^AB forza con cui A attrae B (segno -)
r2
rAB = rB- rA
A
B
r=|rAB| distanza da A a B
FAB
mB mA
FBA= - G ---------- r^BA forza con cui B attrae A (segno -)
r2
A
FBA
B
da notare che vale il principio di azione e reazione
mA mB sono le masse gravitazionali dei corpi, sempre di valore positivo, che
l’esperienza dimostra essere uguali alle loro masse inerziali
G = 6.67259 10-11 N m2/kg2 è la costante di gravitazione universale
G. Bracco - Appunti di Fisica
Generale
5
Forza elettrostatica di Coulomb
E’ la forza che agisce fra ogni coppia di corpi aventi una carica
qA qB
FAB= k ---------- ^rAB forza con cui A interagisce con B
r2
qB qA
^
FBA= k ---------- rBA forza con cui B interagisce con A
r2
qA qB sono le cariche elettriche dei corpi di valore positivo o
negativo
k = 1/(4 πε0) = 8.99 109 Nm2/C2
con ε0 = 8.85 10-12 C2/(Nm2) la costante dielettrica del vuoto
G. Bracco - Appunti di Fisica
Generale
6
3
Al contrario delle forze di attrito che nascono dal contatto fra i corpi
(forze di contatto)
la forza gravitazionale e quella elettrostatica agiscono a distanza
e hanno raggio d’azione infinito.
La loro struttura matematica è identica, inversamente proporzionale
al quadrato della distanza
mA mB
FAB= - G ---------- r^AB
r2
ed agiscono lungo la congiungente fra i corpi.
Esse sono perciò della forma F= f(r) r^AB
e sono dette forze centrali
G. Bracco - Appunti di Fisica
Generale
7
Nella meccanica classica, le forze si trasmettono istantaneamente ma
questo viola che la velocità limite sia quella della luce.
Ciò si modifica introducendo il concetto di campo (funzione (in
questo caso vettoriale) definita in ogni punto dello spazio-tempo)
mA
)
FAB=( - G ---------- r^AB mB= CA mB
r2
Es. con CA campo (gravitazionale in questo caso)
è il campo generato da A che agisce nel punto dove è presente B. Il
campo si propaga con la velocità della luce secondo opportune
equazioni del campo (per la gravità: Relatività generale).
Analogamente per la forza di Coulomb si definisce il campo elettrico
FAB =EA qB ; l’Elettromagnetismo descrive con le eq. di Maxwell come
si comporta il campo elettrico (in genere non disgiunto da quello
magnetico) che vedremo più avanti nel corso.
Altri esempi di campi: velocità di un corso d’acqua, temperatura di
G. Bracco - Appunti di Fisica
8
un corpo, ….
Generale
4
Forza peso
Nel caso frequente in cui il corpo è sulla superficie terrestre la formula generale si
può semplificare considerando
che la distanza dal centro della Terra è in pratica
^
sempre uguale al raggio terrestre R=(6371.01±0.02) km
mA
FAB=( - G -------- rAB ) mB = g mB
r2
con g accelerazione
^ di gravità (la quantità tra parentesi calcolata per r=R) diretta
verso il centro della Terra di massa mA =5.9736x1024 kg
quindi la forza che la Terra esercita su un corpo vicino alla sua superficie (peso) è
P=mg (uguale in modulo alla forza che il corpo esercita sulla Terra?)
Dalla definizione di accelerazione di gravità il modulo varia sia variando quota,
sia per la non perfetta sfericità della Terra, sia per la non omogeneità della Terra
al polo g=9.8321863685 m s-2 all’equatore g= 9.7803267715 m s-2
per i problemi useremo un valor medio
g=9.80625657 m s-2 o con tre cifre significative 9.81 m s-2
G. Bracco - Appunti di Fisica
Generale
9
La forza gravitazionale e quella elettrostatica sono due forze
fondamentali della natura da cui discendono le altre che causano
il moto dei corpi a livello macroscopico. Esistono altre due forze
fondamentali, il cui ruolo è importante a livello subatomico ma i cui
effetti sono anche macroscopici (centrali atomiche ….)
Sono le forze nucleari forti e le forze nucleari deboli.
Le prime tengono uniti i costituenti
del nucleo atomico che sono sia neutri
(neutroni) che carichi (protoni).
I protoni per repulsione elettrostatica
tenderebbero a far esplodere il nucleo
ed è proprio la forza nucleare forte che
li mantiene uniti. La forza debole è
responsabile dei
decadimenti radioattivi
e dei processi di fusione
che avvengono nelle stelle.
G. Bracco - Appunti di Fisica
Generale
10
5
Una breve nota sui costituenti fondamentali della materia:
Per i greci antichi: aria, terra, acqua e fuoco (Empedocle, nel V sec.
a.C )
Poi Democrito (400 a.C.) propose l’idea di atomo, indivisibile e questa
idea rimase per molto tempo. Attorno al 1900, si pensava che gli atomi
fossero fatti come delle palline.
Si vide però che gli atomi potevano essere classificati in base alle loro
proprietà chimiche (come nella tavola periodica): questo fatto lasciava
pensare che non fossero fondamentali. Poi si scoprì l’elettrone e con
esperimenti di diffusione di particelle α si arrivò al concetto di nucleo.
Molti anni dopo, gli scienziati hanno scoperto che il nucleo è
composto: è fatto di protoni (p) e neutroni (n).
I dati sperimentali però hanno mostrato che nemmeno i protoni e i
neutroni sono fondamentali -- sono composti da particelle più
elementari, chiamate quark. Sembra che i quark e gli elettroni siano
fondamentali (?).
G. Bracco - Appunti di Fisica
Generale
11
Adroni: particelle formate da quark
Barioni: Protone (uud) e neutrone (udd)
(up e down, ma anche strange, charmed,
bottom, top). Mesoni: (quark+antiquark)
Leptoni
Come fanno a stare assieme e interagire?
Si è capito che tutte le interazioni (o forze) che riguardano le particelle materiali sono
dovute ad uno scambio di mediatori di forza. Pensiamo al gioco del calcio: i giocatori
sono le particelle materiali che si passano un pallone, questo è la particella mediatrice di
forza che da’ una spinta quando arriva. Quelle che noi chiamiamo comunemente "forze"
sono gli effetti dei mediatori di forza sulle particelle materiali.
G. Bracco - Appunti di Fisica
Generale
Classicamente ad
un mediatore è
associato un campo
di forza.
P.es.
fotone↔campo
12
elettromagnetico
6
La seguente tabella fornisce un ordine di grandezze delle forze in
gioco
Per 2 protoni a distanza di 2 10-15 m
forza
gravità
agisce su
tutte le masse
raggio d’azione
infinito
debole
su quasi tutte le
particelle elementari <10-17 m
intensità
10-34 N
10-2 N
elettromag cariche elettriche
infinito
102 N
forte
10-15 m
104 N
particelle nucleari
G. Bracco - Appunti di Fisica
Generale
13
Forza elastica
Se un corpo viene sollecitato da una forza, almeno inizialmente
le deformazioni sono proporzionali alla forza (legge di Hooke)
p.es. deformazione di una molla:
|F|=k(l-l0) F modulo della forza, k costante elastica della molla
l lunghezza finale della molla, l0 lunghezza a riposo
Supponiamo che un corpo sia vincolato ad una molla di costante
elastica k e che esegua un moto unidimensionale. Fissiamo l’origine
nella posizione di riposo della molla ( l-l0=x ).
m
F
la forza è sempre diretta
O
x
verso O e quindi la
componente F<0 per x>0
X
F
m
X
x
O
G. Bracco - Appunti di Fisica
Generale
F>0 per x<0
da cui
F=-kx
14
7
L’equazione del moto è perciò
ma=-kx ovvero a+ (k/m) x=0
••
x + (k/m) x=0
equazione del moto armonico le cui soluzioni sono del tipo
x=A cos (ωt+φ) con A ampiezza dell’oscillazione
(soluzioni alternative x=A sen (ωt+φ) o x=A cos (ωt) + B sen (ωt+φ) )
ω2= k/m pulsazione del moto, φ fase iniziale
per t=0 s x=A cos(φ) v= - A ω sin(φ) condizioni iniziali
Animazione: molla(phi)
In 3 dimensioni la forza elastica si scrive F = - k (r - r0)
(isotropa in tutte le direzioni)
anche in questo caso si tratta di una forza centrale (rispetto
ad r0 ) come nel caso della forza gravitazionale ed elettrostatica.
G. Bracco - Appunti di Fisica
Generale
15
Attrito viscoso
Il moto di un corpo in un fluido (gas o liquido) incontra una resistenza
che dipende dalla velocità relativa tra corpo e fluido
F=-f(v)v^ con f(v) una funzione della velocità ed il segno - perché la
forza si oppone al moto, si può pensare di sviluppare in serie
f(v)= β v + B v2 + …..
per basse velocità
F= - β v
il coefficiente β è legato alle proprietà del fluido e alle caratteristiche
geometriche del corpo, per una sfera di raggio R: β =6π R η con
η coefficiente di viscosità del fluido.
In aria e con moto turbolento la forza (resistenza aerodinamica)
vale |F|=½CρAv2 con C coefficiente di resistenza aerodinamica,
ρ=massa volumica dell’aria (densità), A=sezione max. del corpo
G. Bracco - Appunti di Fisica
Generale
16
8
In entrambi i casi se un corpo cade soggetto alla gravità si
osserva che la velocità aumenta fino ad un valore limite
Moto unidimensionale:
1)
ma=mg- β v
-βv
la soluzione (costante) a regime è
ma=0 v=mg/ β
x
mg
2)
ma=mg-Bv2
________
ma=0 v=√mg/B con B= ½CρA
Esercizio: trovare le soluzioni per un corpo che parte da fermo e cade
immerso nel fluido.
G. Bracco - Appunti di Fisica
Generale
17
Tensione di una molla: è la forza che agisce su ogni tratto della molla,
in particolare ai suoi estremi. Supponiamo che ci siano due masse agli
estremi. F’+T’=m1 a1 e F+T=m2 a2.
T
F’ T’
F Ma se m →0 m →0 allora F’=-T’e F=-T
1
2
quindi le forze applicate dalla molla
m1
m2
(tensioni) sono uguali e opposte a quelle
che si devono applicare agli estremi per allungarla (o comprimerla)
(forze uguali e opposte) (nella figura la molla è allungata altrimenti tutte
le forze sono opposte).
D’altra parte considerando la molla F’+ F=mmolla amolla, ma se mmolla→0
allora F’=- F cioè la forza ai due estremi è uguale e opposta, quindi la
tensione è uguale e opposta agli estremi T’=-T.
Molla ideale: molla con massa trascurabile che segue la legge di Hooke.
Fune ideale= fune che non si allunga (molla con costante elastica k
infinita per gli allungamenti) e di massa trascurabile. Genera una
tensione uguale e opposta agli estremi (a trazione ma non a spinta).
G. Bracco - Appunti di Fisica
Generale
18
9
La fune determina anche un vincolo sulle posizioni dei corpi che sono
da essa collegati: lo spostamento degli estremi è uguale in modulo (il
segno dipenderà dalla scelta del sistema di riferimento)
Carrucola: essa serve a modificare la direzione della fune che vi si
avvolge attorno e quindi della tensione trasmessa dalla fune.
V
Il perno della carrucola reagisce in modo
da mantenere in quiete la carrucola stessa
(reazione vincolare V).
Se la massa è trascurabile e ruota senza
attriti (carrucola ideale) allora la tensione
si trasmette inalterata, altrimenti la
tensione prima e dopo la carrucola è
differente e la differenza è necessaria per
mettere in rotazione la carrucola
G. Bracco - Appunti di Fisica
Generale
19
Quantità di moto
Si definisce quantità di moto il prodotto p= m v (unità kg m/s)
la seconda legge di Newton si scrive perciò
F= dp/dt (*)
In questa forma essa ha validità anche per sistemi a massa variabile
(p.es. razzi) o per estendere la meccanica classica anche al caso
relativistico in cui la massa di un corpo varia con la velocità o per il
processo di quantizzazione della meccanica quantistica.
Si definisce impulso di una forza (nell’intervallo t1,t2) la quantità
J=∫F dt l’integrale è calcolato fra (t1,t2). Dalla (*) si può pertanto
scrivere ∫dp =∫F dt cioè fra (t1,t2),
∆p=J Teorema dell’impulso
G. Bracco - Appunti di Fisica
Generale
20
10
Momento di una forza e
momento della quantità di moto (momento angolare)
Per trattare i moti, in particolare le rotazioni, è opportuno introdurre
il concetto di momento di una forza (o torcente, unità Nm).
Consideriamo il momento rispetto all’origine degli assi (polo)
t=r×F e
momento della quantità di moto (o momento angolare) (unità kg m2 /s)
l = r × p = r × mv
deriviamo rispetto al tempo
dl/dt=d(r × p )/dt = dr/dt× p + r × dp/dt = v × p + r × dp/dt = r × F
poiché v e p sono paralleli, da cui
t=dl/dt
G. Bracco - Appunti di Fisica
Generale
21
Se scegliamo un altro punto r0 (polo) rispetto a cui calcolare i momenti
t0 = (r- r0) × F
e momento della quantità di moto
l0 = (r- r0) × p = (r- r0) × mv
deriviamo rispetto al tempo
dl0/dt=d((r- r0) × p )/dt = d (r- r0) /dt× p + (r- r0) × dp/dt =
v × p - dr0/dt × p + (r- r0) × dp/dt = -v0 × p + (r- r0) × F
poiché v e p sono paralleli, se il punto r0 è fisso si ha ancora
t0=dl0/dt (altrimenti t0=dl0/dt + v0 × p )
r- r0
r
0
r
G. Bracco - Appunti di Fisica
Generale
22
11
Conservazione del quantità di moto e
e del momento angolare
Se la risultante delle forze su un corpo è nulla allora
dp/dt=0 cioè p è costante: conservazione della quantità di moto
Se il momento risultante è nullo
dl/dt=0 cioè l è costante: conservazione del momento angolare
queste leggi di conservazione sono soprattutto utili nel caso di
sistemi formati da più punti materiali. Esse sono di grande
importanza poiché hanno validità generale e sono legate
all’omogeneità (un fenomeno non cambia se si trasla il sistema di
riferimento) e isotropia (un fenomeno non cambia se si ruota il
sistema di riferimento) dello spazio.
Es. nel caso di forze centrali il momento angolare si conserva
r×f(r) r^ =0 poiché sono vettori paralleli
G. Bracco - Appunti di Fisica
Generale
23
Esercizio:
Una pallina di massa m=2.0 kg è vincolata a muoversi nel piano xy.
Se la sua velocità è |v| =5.0 m/s diretta come la bisettrice del primo
quadrante per valori di x crescenti, calcolare la sua quantità di moto
ed il suo momento angolare rispetto all’origine e rispetto ad punto
P=(0.0 , 2.0) m.
Una pallina di massa m=3.0 kg sta eseguendo nel piano xy la
traiettoria descritta da:
x=2 cos(2 t)
y=2t2, calcolare il tipo di curva che sta descrivendo, la risultante
delle forze ad essa applicata, la quantità di moto ed il momento
angolare rispetto all’origine per t=1.0 s.
G. Bracco - Appunti di Fisica
Generale
24
12