Recupero estivo n°2

1^A - Esercitazione recupero n°2
1. Un cavo di nylon si comporta come una molla di costante elastica 5,0⋅10 4 N / m . Con questo
cavo, trasciniamo sul pavimento una cassa di 280 kg a velocità costante. Il coefficiente di
attrito dinamico tra la cassa e il pavimento è 0,11. Calcola il valore della forza di attrito che si
esercita tra la cassa ed il pavimento. Di quanto si allunga il cavo mentre si trascina la cassa?
[3,0⋅102 N ; 6,0 mm]
2. Un elastico lungo 10 cm viene allungato di 1,5 cm . La distanza media tra due atomi del
nastro elastico è di 0,4 nm . Qual è l'aumento medio della distanza tra un atomo e l'altro lungo
la direzione di allungamento?
−2
[6⋅10 nm]
3. Uno sciatore di massa 82 kg sta scendendo un pendio, la cui inclinazione è 30°. Calcola
l'intensità delle componenti della forza peso parallela e perpendicolare al pendio.
2
2
[4,0⋅10 N ; 6,9⋅10 N ]
4. Seguendo la mappa di un tesoro, un pirata cammina per 2,00 km verso Nord-Est, poi per 3,00 km
verso Est, quindi per 3,00 km verso Sud-Est ed infine per 2,00 km verso Ovest. Arrivato al
termine del percorso, a quale distanza dalla posizione di partenza si trova il pirata?
[ 4,59 km]
5. Una molla, disposta in orizzontale, ha un'estremità fissata ad una parete e
l'altra attaccata ad una cassa. La costante elastica della molla è di
6,0⋅102 N / m , il suo allungamento misura 21 cm , la massa della cassa
è di 20 kg ed il valore del coefficiente di attrito statico tra la cassa e il pavimento è 0,75 .
Quanto vale la forza esercitata dalla molla sulla cassa? Qual è il massimo valore della forza di
attrito statico tra la cassa ed il pavimento? In queste condizioni, la forza elastica fa muovere la
cassa? Qual è il massimo allungamento della molla per il quale la cassa continua a rimanere in
equilibrio?
[1,3⋅10 2 N ;1,5⋅10 2 N ; no ; 25 cm]
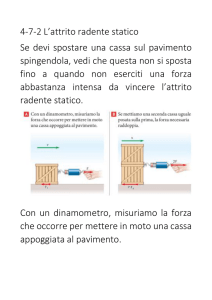
6. Una molla, disposta in orizzontale, ha un estremo fissato ad un muro e l'altro legato ad un
mattone che pesa 27 N . La costante elastica della molla è k =180 N / m ed il coefficiente di
attrito radente statico tra il mattone ed il pavimento vale 0,90 . Si afferra il mattone e lo si fa
strisciare sul pavimento fino ad allungare la molla di 20 cm . Quali sono i moduli della forza
elastica e della forza di primo distacco tra mattone e pavimento? Se lasciamo andare il mattone,
questo si mette in moto?
[36 N ; 24 N ; sì ]
7. Uno scivolo di un parco giochi è alto 1,8 m e lungo 4,5 m . Su di esso si trova un bimbo che
ha una massa m=28 kg . Trascurando l'attrito con lo scivolo, con quale forza il bimbo si deve
afferrare al bordo dello scivolo per rimanere fermo?
[110 N ]
8. Un'automobile è ferma su una strada in discesa, con il freno a mano tirato. La pendenza della
strada è del 10% (ovvero, la strada sale di 10 m ogni 100 m di percorso). La massa
dell'automobile è di 840 kg . Qual è il valore della forza di attrito sugli pneumatici che tiene
[8,2⋅10 2 N ]
ferma l'automobile?
9. Per tenere in equilibrio un carrello della spesa su un piano inclinato lungo 4,00 m e alto
[ 4,9⋅102 N ]
0,75 m , è necessaria una forza di 92 N . Quanto pesa il carrello?
10.La rampa di carico di un magazzino permette di superare un dislivello di 1,5 m . Su di essa è
fermo un carrello, la cui massa è di 130 kg . Per trattenere il carrello occorre esercitare una
[21 m]
forza parallela alla rampa di 91 N . Qual è la lunghezza della rampa?
11.Un facchino sta tenendo ferma una cassa di 33,5 kg , appoggiata su una passerella inclinata alta
2,40 m e lunga 10 m . Se trascuriamo l'attrito, qual è il valore della forza equilibrante
necessaria a tenere la cassa in equilibrio? Qual è il modulo della forza di reazione vincolare del
[78,8 N ; 318 N ]
piano?
Se, invece, il coefficiente di attrito statico tra la cassa e la passerella è 0,150, quali sono la
direzione, il verso ed il modulo della forza di attrito statico? Quanto vale la forza che il facchino
deve esercitare per tenere in equilibrio la cassa?
[ 47,7 N ; 31,1 N ]
12.Due operai devono trasportare una cassa del peso di 1000 N , appoggiata su un'asta lunga
2,0 m e di peso trascurabile. La cassa dista 80 cm da uno dei due operai. Quanto valgono le
intensità delle forze che i due operai devono applicare per poter sostenere la cassa?
[400 N ; 600 N ]
13.Un bambino è seduto ai due estremi di un'altalena a 2,12 m dal fulcro centrale. Il padre lo fa
giocare premendo l'altro braccio dell'altalena a 1,56 m dal centro. Il peso del bambino è
170 N . Quale forza deve esercitare il padre, in direzione perpendicolare all'altalena, per fare in
modo che questa rimanga in posizione orizzontale e non ruoti? Perché questa forza risulta
[231 N ]
maggiore del peso del bambino?
14.Una leva è sottoposta all'azione di una forza resistente di F
m
12 N . Qual è l'intensità della forza motrice in grado di
32 cm
equilibrare la forza resistente? Di che genere è la leva? E'
vantaggiosa o svantaggiosa?
8,0 cm
Fr=12N
[ 2,4 N ]
fulcro
15.Per far ruotare un bicchiere su se stesso, applichiamo sull'orlo con le dita di una mano due forze
uguali e opposte, in punti diametralmente opposti e in modo che le due forze siano tangenti
all'orlo stesso. Il raggio del bicchiere è di 36 mm e ciascuna delle forze ha un'intensità di
1,5 N . Determina il momento della coppia applicata al bicchiere.
[0,11 N⋅m]
16.Due persone spingono sui lati opposti di una porta. Il primo preme a 62 cm dai cardini, con una
forza di intensità 740 N . Il secondo spinge a 78 cm dai cardini, con una forza di 620 N .
Quanto valgono i momenti delle forze esercitate? Da che parte gira la porta?
[ 460 N⋅m ; 480 N⋅m]
1^A - Correzione esercitazione n°2
1. Se un corpo si muove con velocità costante, significa che la risultante delle forze applicate al
corpo è nulla. Nel nostro caso, la forza elastica dovuta al cavo di nylon è uguale ed opposta alla
forza di attrito dinamico tra cassa e pavimento.
Forza di attrito: F att =d P= m g≃0,11⋅9,8
Allungamento:  x=
N
⋅280 kg ≃300 N .
kg
F
300 N
≃
≃6⋅10−3 m .
4
k 5,0⋅10 N / m
2. In un corpo elastico, l'allungamento di una parte qualunque del corpo è direttamente
proporzionale alla sua lunghezza. Quindi:
x
1,5 cm
1,5 cm
=
⇒  x=
⋅0,4 nm=0,06 nm .
0,4 nm 10 cm
10 cm
3. Il triangolo formato dalla forza peso e dalle sue componenti
P║
parallela e perpendicolare al piano inclinato è simile a quello
P
descritto dal piano inclinato, in quanto gli angoli di entrambi
a
P┴
a=30°
misurano 30°, 60° e 90°.
Di conseguenza, i loro lati sono in proporzione, ed abbiamo:
P ∥ =mg sen ≃82 kg⋅9,8
N 1
⋅ ≃400 N ; P
kg 2
⊥
=mg cos ≃82 kg⋅9,8
N 3
⋅ ≃700 N .
kg 2
4. Considero un sistema di riferimento avente l'origine nel punto di partenza del pirata, l'asse x
rivolto verso Est e l'asse y rivolto verso Nord. Rispetto a questo sistema di riferimento, i quattro
spostamenti hanno rispettivamente componenti (espresse in km):
s1≡2 cos 45 ° , 2 sen 45° ≡  2 ,  2 ; s2≡3 , 0 ;
s3≡−3 cos 45° ,−3 sen 45 ° ≡
3
3
2 ,−  2 ; s2≡−2 , 0 .

2
2
Lo spostamento complessivo ha come componenti la somma algebrica delle componenti dei
singoli spostamenti:
s x =  23
3
5
3
1
2−2=1  2≃4,54 ; s y =  2−  2=−  2≃−0,71 .

2
2
2
2
Spostamento complessivo: s=  s 2x s 2y ≃  4,54 20,712≃4,60 km .
2
5. Forza esercitata dalla molla sulla cassa: F el =k el  x=6,0⋅10
N
⋅0,21 m≃130 N .
m
Massimo valore della forza di attrito statico: F att =s mg≃0,75⋅20 kg⋅9,8
N
≃150 N .
kg
La forza elastica non fa muovere la cassa, in quanto il suo modulo è inferiore al massimo valore
che può essere assunto dalla forza di attrito statico.
La cassa continua a rimanere in equilibrio fino a che:
F el ≤F att ⇒ k el  x≤ s m g ⇒  x≤
6. Forza elastica: F el =k el  x=180
s m g 0,75⋅20 kg⋅9,8 N / kg
≃
≃0,25 m .
k el
6,0⋅10 2 N / m
N
⋅0,2 m=36 N .
m
Forza primo distacco: F att = s P=0,90⋅27
N
≃24 N .
kg
Il mattone si mette in movimento, in quanto la forza elastica supera quella di primo distacco.
7. Come nell'esercizio 3, dimostriamo che il triangolo formato
P║
dalla forza peso e dalle sue componenti parallela e
l
perpendicolare al piano inclinato è simile a quello descritto
F
P
P┴
h
dal piano inclinato, in quanto essi hanno gli angoli
ordinatamente uguali. Di conseguenza, i lati sono in proporzione, ed abbiamo:
P∥ h
h
1,8 m
N
= ⇒ P ∥ = ⋅mg≃
⋅28 kg⋅9,8 ≃110 N .
P
l
l
4,5 m
kg
La forza F esercitata dal bambino deve essere uguale ed opposta a P
8. Il fatto che la pendenza sia del 10% significa che il rapporto
∥
.
h
=0,1 .
l
Ragiono come nell'esercizio precedente:
P∥ h
h
N
= ⇒ P ∥ = ⋅mg≃0,1⋅840 kg⋅9,8 ≃820 N .
P
l
l
kg
La forza di attrito tra pneumatici e suolo deve essere uguale ed opposta a P
9. Ho ancora la proporzione:
∥
.
P∥ h
= , ma, in questo caso, l'incognita è il peso del carrello.
P
l
l
4,00 m
⋅92 N ≃490 N .
Quindi: P= P ∥ =
h
0,75 m
10.In questo caso, l'incognita è la lunghezza del piano inclinato.
P∥ h
mg
130 kg⋅9,8 N / kg
= ⇒ l=
h≃
⋅1,5 m≃21 m .
P
l
P∥
91 N
P∥ h
h
2,40 m
N
= ⇒ P ∥ = ⋅mg≃
⋅33,5 kg⋅9,8 ≃78,8 N .
P
l
l
10 m
kg
11.Trascurando l'attrito:
La reazione vincolare del piano è uguale ed opposta alla componente della forza peso
perpendicolare al piano stesso:
P
⊥

=  P 2−P 2∥ ≃ 33,5 kg⋅9,8
N 2
 −78,8 N 2≃318 N .
kg
In presenza di attrito statico, esso ha direzione parallela al piano inclinato, verso opposto a quello
di P
∥
e modulo massimo: F att = s P
Poiché l'attrito massimo è minore di P
⊥
∥
≃0,150⋅318
N
≃47,7 N .
kg
, il facchino deve ancora esercitare una forza pari a:
F =P ∥ −F att ≃78,8−47,7≃31,1 N .
12.La situazione è quella rappresentata in figura.
Poiché i due operai sostengono la cassa senza farla ruotare, i
momenti delle forze che essi esercitano sono uguali ed
F1
F2=P-F1
l2=120 cm
opposti:
F 1 l 1= P−F 1 l 2 ⇒ 80 F 1=1000⋅120−F 1⋅120 ⇒
l1=80 cm
P=1000 N
⇒ 200 F 1=120.000 ⇒ F 1=600 N .
Di conseguenza: F 2=P−F 1=1000−600=400 N .
13.Impongo che i momenti delle forze siano uguali ed opposti:
F 1 l 1=F 2 l 2 ⇒ F 1=
l2
2,12 m
F 2=
⋅170 N ≃231 N .
l1
1,56 m
La forza che deve esercitare il padre è maggiore del peso del bambino, in quanto il braccio della
forza applicata dal padre è minore rispetto al braccio della forza peso del bambino.
14.Impongo che i momenti delle forze siano uguali ed opposti:
F m l m=F r l r ⇒ F m=
lr
8,0 cm
F r=
⋅12 N ≃2,4 N .
lm
40 cm
La leva è del secondo genere, in quanto la forza resistente si trova tra il fulcro e la forza motrice,
e, di conseguenza, è sempre vantaggiosa.
15. M =F d =1,5 N⋅7,2⋅10−2 m≃0,11 N⋅m .
16. M 1=F 1 d 1=740 N⋅0,62 m≃460 N⋅m ;
M 2=F 2 d 2=620 N⋅0,78 m≃480 N⋅m .
La porta si apre nel verso in cui spinge la seconda persona.
F
r
F