Regime sinusoidale

Regime
sinusoidale
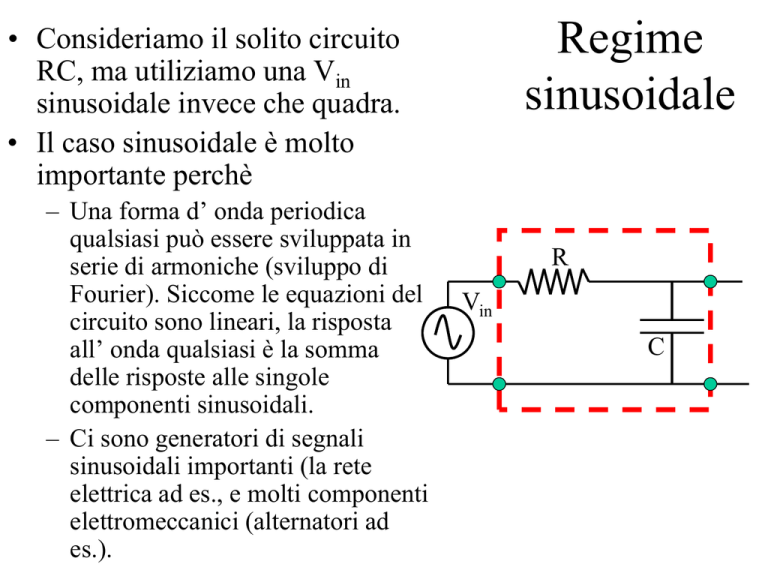
• Consideriamo il solito circuito
RC, ma utiliziamo una Vin
sinusoidale invece che quadra.
• Il caso sinusoidale è molto
importante perchè
– Una forma d’ onda periodica
qualsiasi può essere sviluppata in
serie di armoniche (sviluppo di
Fourier). Siccome le equazioni del
circuito sono lineari, la risposta
all’ onda qualsiasi è la somma
delle risposte alle singole
componenti sinusoidali.
– Ci sono generatori di segnali
sinusoidali importanti (la rete
elettrica ad es., e molti componenti
elettromeccanici (alternatori ad
es.).
R
Vin
C
Regime
sinusoidale
Vin  Vo cos(t )
dQ Q
V (t )  R
 0
dt C
dVC
V (t )  RC
 VC  0
dt
dVC
RC
 VC  Vo cos(t )
dt
si cerca una soluzione del tipo
VC  VoC cos(t   )
Sostituendo si trovano le costanti
VoC e 
R
Vin
C
Regime
sinusoidale
si preferisce pero' usare la notazione
complessa, che rende piu' semplici
i calcoli. Si usa l' identita'
R
e j  cos( )  j sin( )
e si considera, convenzionalmente,
l' equazione per V(t) come la parte
reale di una equazione complessa :
Vin
C
Quindi :
VC  VoC e j (t  )
e Vin  Vo e jt e quindi
dVC
RC
 VC  Vo cos(t )  RCjVoC e j (t  )  VoC e j (t  )  Vo e jt
dt
Regime sinusoidale
RCj  V oC e j ( t   )  V oC e j ( t   )  V o e j t
RCj  V oC e j t e j  V oC e j t e j  V o e j t
RCj  V oC e j  V oC e j  V o
V oC e
j
V oC 
Vo

RCj   1
Vo
RC  
2
1
e quindi
R
Vin
C
Regime sinusoidale
inoltre si puo' anche scrivere
Vo
Vo
j
1  jRC  
V oC e 

2
RCj   1 ( RC  )  1




 Im V oc e j 
 si trova subito
usando il fatto che   arctan 
j 
 Re V oc e 
 RC  
  arctan  
  arctan  RC    arctan   
1 

R
Vin
C
• Possiamo quindi graficare, inRegime sinusoidale
funzione della frequenza del
segnale d’ ingresso, l’ ampiezza
del segnale in uscita, ed il suo
R
sfasamento:
Vin
Vin  Vo e jt

C
Vout  VoC e j (t  )
Vo
Vo / 2
dove
VoC 
Vout
Vo
   1
  arctan   
2
0
VoC
0
1
2
3
4
5
6
RC
0 0
1
2
3
4
5
6
RC

/4
/2
Regime sinusoidale
• Per  0 la tensione ai capi
del condensatore tende ad
essere in ogni istante uguale
a quella del generatore:
condizioni quasistatiche
• Per   le variazioni di
tensione in ingresso sono
talmente veloci che il
condensatore non riesce né a
VoC
Vo
caricarsi né a scaricarsi in
tempo. Di conseguenza la Vo / 2
tensione ai suoi capi rimane
0
nulla.
0

• Per  intermedi, la tensione
del condensatore segue, con
0 0
un certo ritardo e ridotta in
/4
ampiezza, la tensione di
/2
ingresso.
R
Vin
Vout
C
1
2
3
4
5
6
RC
1
2
3
4
5
6
RC
Regime sinusoidale
• Possiamo dire quindi che
le pulsazioni  molto
minori di 1/RC (frequenze
R
molto minori di 1/(2RC))
passano attraverso il
Vin
blocco RC, mentre le
C
pulsazioni  molto
maggiori di 1/RC non
VoC
passano attraverso il
Vo
blocco RC.
Vo / 2
• Si conclude che, quando si
prende il segnale in uscita
0
0
1
2
3
4
5
ai capi del condensatore, il

blocco RC si comporta
come un filtro passa basso
0 0
1
2
3
4
5
• La frequenza fo=1/(2RC) /4
viene detta frequenza di
/2
taglio del filtro.
O.D.G.: R=1k, C=1F, fo=0.16 kHz
Vout
6
RC
6
RC
I fasori
• Alla rappresentazione complessa delle tensioni
corrisponde una rappresentazione geometrica
interessante.
• Nel piano complesso i segnali
Vin  Vo cos(t )
 Vin  Vo e jt
VC  VoC cos(t   )  VC  VoC e
j(t  )
• Sono vettori che ruotano in senso antiorario con
velocità :
VC  VoC e j(t  )
Im(Vin)
Im(V)
jt
Vosin(t)
Vin  Vo e

t
Vocos(t)
Re(Vin)
t+
Vin  Vo e jt
t
Re(V)
Corrente
• La corrente che scorre nel circuito … è


dq
dV C
d
i
VoC e j (  t  )  CV oC j  e j (  t  )
C
C
dt
dt
dt
Legge di Ohm Generalizzata:
iC  i   j  C  VC
basta pensare ad una “impedenza“
del condensatore pari a 1/jC
j  CV in
i  j  CV C 
RCj   1
scrivendo la corrente nella forma i  I o e j (  t  I ) si ottiene :
I o  Vo
C
1  
 I  arctan(
1

)
2
io
io / 2
0
0
/2 
1
2
3
4
5
6
RC
0 0
1
2
3
4
5
6
RC
/4
Corrente
• La corrente che scorre nel circ. durante la carica e scarica
del condensatore è
dV C
d
dq
C
 C VoC e j ( t  )   CV oC j e j ( t  )
i
dt
dt
dt
Legge di Ohm Generalizzata:
iC  i   j C  VC
basta pensare ad una “impedenza“
j CV in
del condensatore pari a 1/jC
i  j CV C 
RCj   1
scrivendo la corrente nella forma i  I o e
Io 
C
1   
 I  arctan(
2
1

)
Vo
da
confrontare
con
j ( t   I )
VoC 

VC
si ottiene :
1
1   
2
Vo
 arctan( )
Corrente
• La corrente nel circuito è quindi sfasata rispetto alla tensione ai
capi del condensatore:
1
 
tan  I   tan  V C
 
 
tan(  I   V C ) 
1  tan  V C tan  I  1   1

• Quindi
 
 I  V 
C
 

2
• La tensione ai capi del condensatore ha un ritardo di 90o rispetto
alla corrente, indipendentemente dalla frequenza.
Im
Vc
I
V
t
Ic
/2
Re
Corrente
• Con la notazione complessa si ritrova subito lo stesso risultato
da iC  i   jC  VC
VoC e
VoC e
j (t V )
C
jV
C

j
1
1
1
j (t  I )
j (t  I )
2

I oe
j
I oe
e
I o e j (t  I )
C
C
j C
I o j ( I  2 )

e
C
Im
  I  VC 
Vc
I

2
V
t
Ic
/2
Re
L’ oscilloscopio
• è lo strumento più utilizzato per studiare grandezze elettriche variabili nel tempo.
• Ha uno schermo sul quale viene visualizzato il grafico della grandezza in funzione del tempo:
• Grazie ai comandi accessori possono essere variate le scale del grafico in un grande intervallo di valori, in modo da visualizzare segnali lenti o veloci, di grande o piccola ampiezza.
monitor
V(t)
t
Y(V/cm)
X(ms/cm)
comandi
L’ oscilloscopio analogico
• Nell’ oscilloscopio analogico la visualizzazione viene ottenuta focalizzando un fascetto di elettroni in diversi punti di uno schermo ricoperto di materiale fosforescente. Arrivando nel centro dello schermo gli elettroni cedono la loro energia agli atomi del fosforo, che poi si diseccitano producendo fotoni e generando così un puntino luminoso.
Tubo a raggi catodici:
F
Tubo sotto vuoto (vetro)
fosforo
Fascetto di elettroni
Punto
luminoso
A1 A2 A3
– F=filamento, C=catodo, A1,A2,A3=anodi
• Gli elettroni, emessi dal filamento incandescente, vengono accelerati dagli anodi fino a circa 1 keV.
C
L’ oscilloscopio analogico
• La posizione del punto luminoso sullo schermo può essere modificata deviando la traiettoria del fascetto di elettroni all’ interno del tubo.
• Ad esempio, applicando un campo elettrico ortogonale al fascetto, si esercita una forza in direzione ortogonale alla traiettoria, deviando il fascetto.
Y
X
F
C
A1 A2 A3
L’ oscilloscopio analogico
• La posizione del punto luminoso sullo schermo può essere modificata deviando la traiettoria del fascetto di elettroni all’ interno del tubo.
• Ad esempio, applicando un campo elettrico ortogonale al fascetto, si esercita una forza in direzione ortogonale alla traiettoria, deviando il fascetto.
Y
X
F
C
A1 A2 A3
E
Z
L’ oscilloscopio analogico
• La posizione del punto luminoso sullo schermo può essere modificata deviando la traiettoria del fascetto di elettroni all’ interno del tubo.
• Ad esempio, applicando un campo elettrico ortogonale al fascetto, si esercita una forza in direzione ortogonale alla traiettoria, deviando il fascetto.
Y
VY
X
F
C
A1 A2 A3
E
Z
• La deviazione lungo Y può essere ottenuta facendo passare il fascetto tra le due armature di un condensatore (parallele a XZ) al quale viene applicata una tensione VY.
L’ oscilloscopio analogico
• La posizione del punto luminoso sullo schermo può essere modificata deviando la traiettoria del fascetto di elettroni all’ interno del tubo.
• Ad esempio, applicando un campo elettrico ortogonale al fascetto, si esercita una forza in direzione ortogonale alla traiettoria, deviando il fascetto.
VX
F
C
Y
E
X
Z
A1 A2 A3
• La deviazione lungo X può essere ottenuta facendo passare il fascetto tra le armature di un altro condensatore (parallelo a ZY) al quale viene applicata una tensione VX.
L’ oscilloscopio analogico
• Nel tubo catodico sono presenti ambedue i condensatori (detti placchette di deflessione). • Combinando opportunamente le tensioni Vx e Vy si può spostare il puntino luminoso in un punto qualsiasi dello schermo.
VY
VX
Y
X
F
C
Z
A1 A2 A3
• Le deflessioni sono proporzionali alle tensioni Vx e Vy
applicate alle placchette.
L’ oscilloscopio analogico
• Colleghiamo adesso la deflessione sullo schermo alla differenza di potenziale applicata alle placchette di deflessione. • L’ elettrone esce dal catodo e viene accelerato dagli anodi. Se l’ ultimo anodo si trova ad un potenziale Vo, l’ elettrone acquista una energia E=eVo. E quindi uscirà dal cannone elettronico con una velocità data da 1 2
mv  eVo
2

2eVo
v
m
• Continuerà a muoversi con questa velocità nel vuoto del tubo a raggi catodici finchè non entrerà nel campo elettrico presente tra le placchette di deflessione.
Vo
F
C
v
A1 A2 A3
E
L’ oscilloscopio analogico
• Il campo sarà E=Vy/d
• Nel campo l’ elettrone subirà una forza diretta lungo l’ asse y
(ortogonale alle sua velocità iniziale) e quindi la traiettoria viene deflessa. Siccome la forza è costante, il moto è uniformemente accelerato lungo y, mentre è uniforme lungo z:
y  12 a y t
2
con
Fy
eE eVy


ay 
m
m md
z  v ot
2
eVy m 2 1 V y 2
z
1
1
• Eliminando t si ottiene y  2 a y 2  2
z 
z
vo
md 2eVo
4d Vo
Vo
F
C
Y
v
A1 A2 A3
E
d
l
L
L’ oscilloscopio analogico
• All’ uscita delle placchette (dopo una distanza l lungo l’ asse z) l’ elettrone si sarà spostato lungo Y di una quantità
1 Vy 2
y (l ) 
l ed uscirà con un angolo
4d Vo
 1 Vy 
1 Vy
d  1 Vy 2 
 
z  
z  
l
dz  4d Vo  z l  2d Vo  z l 2d Vo
z l
• Quindi dopo una ulteriore distanza L si sposterà ulteriormente lungo Y di Ltg, ed arriverà sullo schermo ad una distanza dal centro Y=Ltg +y(l)
dy
tg ( ) 
dz
Vo
F
C
Y
v
A1 A2 A3
E
d
l
L
L’ oscilloscopio analogico
• Si ottiene quindi
1 Vy 2
1 Vy
1 l
Y  y(l )  Ltg ( ) 
l L
l
2d Vo
4d Vo
2d Vo

l
 2  L  Vy


Y  D Vy
• La deflessione Y è quindi proporzionale alla differenza di potenziale Vy. Lo stesso di scorso si può fare per X. La costante D è detta fattore di deflessione (in cm/V) e può essere regolata tramite i comandi frontali dell’ oscilloscopio.
Vo
F
C
Y
v
A1 A2 A3
E
d
l
L
L’ oscilloscopio analogico
• Normalmente si vuole studiare una tensione variabile nel tempo V(t). Lo si fa connettendola all’ ingresso verticale, in modo che la deflessione verticale del punto luminoso sullo schermo sia
Y  DY V (t )
• Contemporaneamente viene generata internamente all’ oscilloscopio una tensione Vx a dente di sega:
X  DX t
• Quindi la tensione da studiare provoca lo spostamento verticale del punto luminoso, e contemporaneamente questo si sposta a velocità costante orizzontalmente. Il risultato è un grafico della tensione in funzione del tempo. • Ovviamente, il fattore di deflessione orizzontale va regolato in modo da poter osservare tutte le variazioni del segnale V(t), e quello verticale va regolato in modo che l’ ampiezza della deflessione sia sufficiente alla visualizzazione.
Vy(t)
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Vy(t)
X
t
Se la V(t) è periodica
e la Vx(t) ha lo stesso
periodo, il fascetto
ripercorrerà esattamente
lo stesso percorso nel
periodo successivo.
Vy(t)
X
t
Questo viene fatto
moltissime volte
al secondo, e a causa
della persistenza dell’
immagine sulla retina,
si vede un disegno stabile
Vy(t)
X
t
L’ oscilloscopio analogico
• è quindi essenziale sincronizzare il periodo del dente di sega a quello dell’ onda in esame.
• Periodo non sincronizzato:
• Periodo sincronizzato:
L’ oscilloscopio analogico
• C’è un circuito all’interno dell’oscilloscopio detto “circuito di trigger”, che risolve questo problema.
• Il circuito confronta il livello e la pendenza del segnale d’ ingresso con dei valori di riferimento che si possono impostare.
V(t)
VTrigger
L’ oscilloscopio analogico
• C’è un circuito all’ interno dell’ oscilloscopio detto “circuito di trigger”, che risolve questo problema.
• Il circuito confronta il livello e la pendenza del segnale d’ ingresso con dei valori di riferimento che si possono impostare.
V(t)
VTrigger
T
L’ oscilloscopio analogico
• Il “circuito di trigger” fa partire il dente di sega tutte le volte che il livello del segnale e la sua pendenza sono quelli impostati.
• In questo modo si sincronizza il dente di sega al segnale
V(t)
VTrigger
T
L’ oscilloscopio analogico
• Il modo migliore per imparare ad usarlo è lavorarci ! L’ oscilloscopio che avrete a disposizione è un National VP‐
5220A, o ISO‐TECH ISR 622 oscilloscopio a due canali.
• Si possono visualizzare contemporaneamente due segnali indipendenti, chiamati canale 1 e canale 2:
V1(t)
V2(t)
L’ oscilloscopio analogico
• Di solito la prima cosa da fare è verificare i comandi di “trigger”.
• INT‐LINE‐EXT
– Su INT funziona il circuito di trigger che sincronizza automaticamente il dente di sega al segnale
– Su LINE il dente di sega è sincrono con la tensione di rete a 50 Hz
– Su EXT il dente di sega è sincrono con un segnale applicato dall’ esterno, ad un apposito “ingresso di Trigger”
• NORM‐CH1‐CH2
– Permette di selezionare il segnale a cui sincronizzare il dente di sega. Se il canale di interesse è l’ 1, si userà CH1, sennò CH2: nei due casi il trigger è il segnale applicato all’ ingresso scelto. Su norm la sorgente è il segnale visualizzato sul tubo a raggi catodici.
L’ oscilloscopio analogico
• LEVEL, FIX, SLOPE controlla il valore della tensione di riferimento del trigger e la pendenza di riferimento. Quando è completamente ruotato in senso orario, su FIX, è regolato in modo automatico. Si può tirare la manopola o spingerla per selezionare la pendenza; girandola si regola il livello.
• La prima cosa da fare è mettere il trigger su auto: questo permetterà di vedere il segnale, anche se non sincronizzato, e di regolare così le deflessioni verticale e orizzontale. • Una volta visualizzato il segnale, se non è sincrono, si potrà utilizzare il trigger interno regolando livello e pendenza.
Velocità del dente di sega, da 0.5s a 0.2 s per quadretto
Fattore di deflessione
Verticale canale 1 (da 2V a 1 mV per divisione)
Fattore di deflessione
Verticale canale 2 (da 2V a 1 mV per divisione)
Circuito di TRIGGER
Uso dell’ Oscilloscopio
• La prima cosa da fare è mettere su “cal” i potenziometri di taratura dei fattori di deflessione e della base dei tempi (cerchiati di verde nella figura). Vanno ruotati completamente in senso orario.
Uso dell’ oscilloscopio: la seconda cosa da fare è regolare lo zero delle tracce: Si mette il trigger su AUTO
Si mettono a zero i segnali in ingresso a CH1 e CH2, commutando su GND i pulsanti identificati in rosso
Si regola la posizione orizzonatale delle tracce con il potenziometro identificato in azzurro
Uso dell’ oscilloscopio
Traccia regolata sullo zero per entrambi i canali
Uso dell’ Oscilloscopio
• A questo punto si rimettono i commutatori di ingresso su DC (indicati in azzurro)
• Regolando il fattore di deflessione verticale (identificato in rosso) si dovrebbero vedere i due segnali.
Due metodi possibili:
Su auto/norm si grafica
V(CH1) e V(CH2) in
funzione di t
Su X‐Y si grafica
V(CH1) in funzione di V(CH2) e quindi si vede una ellisse:
A(f)=Vout/Vin
Vin
Vout
A(f)=Vout/Vin
Vin
Vout
Metodo più furbo
(f)=2t/T
t
T
(f)=2t/T
t
T
Metodo più furbo
Metodo dell’ ellisse
• Si applicano i segnali ai due assi ortogonali.
X  VX cos t
Y  VY cos(t   )
• Eliminando t viene una eq. Y(X) di una ellisse.
sin(f)=a/b=c/d
b
a
c
d
Oscilloscopio analogico collegato con uscita a 50 Ohm del
Generatore di funzioni Uscita TTL del Generatore di funzioni
Dal manuale dell’oscilloscopio analogico ISO‐TECH ISR 622
Dal manuale dell’oscilloscopio iso-tech-622
Dal manuale dell’ iso-tech isr 622
Oscilloscopi Digitali
• Sono sempre più diffusi. • Invece di deflettere il fascetto elettronico, la tensione in ingresso viene campionata da un convertitore analogico‐
digitale e visualizzata sullo schermo di un piccolo computer.
• Sono molto comodi, con automatismi di configurazione e di misura, ma hanno qualche limitazione dovuta al campionamento e alla quantizzazione (vedi laboratorio anno prossimo). Impedenza Complessa • Riprendiamo il circuito RC:
V in ( t )  RI  V C  0

1
V o  Ri o e j  
io e
j C

1

 R 
j C


 i o e

R
j
Vin
C
j
• Quindi la variabile complessa che rappresenta la corrente è proporzionale alla variabile complessa che rappresenta la tensione; la costante di proporzionalità è un numero complesso, detto “impedenza del circuito”.

1 

Z   R 
j C 

• In questo caso, l’ impedenza del circuito è la somma delle impedenze di R e di C, perchè sono in serie.
Impedenza Complessa 
ZR  R
• Legge di Ohm generalizzata:
 
V Z I

1
ZC 
jC
• Se vogliamo la tensione ai capi del condensatore, ci ricorderemo ancora una volta del partitore e lo scriveremo per le impedenze:



ZC
 Vin 
VC  
ZC  Z R
1
j C
1
j C
R

Vin 

1
Vin
1  Rj  C
• Se vogliamo la tensione ai capi della resistenza, avremo :



ZR
 Vin 
VR  
ZC  Z R

R
Rj  C 
Vin 
Vin
1
1  Rj  C
j C  R
I circuiti RC e CR come filtri
• Quindi quando si prende l’ uscita ai capi del condensatore, il circuito RC si comporta come filtro passa basso:
• Invece quando si prende l’ uscita ai capi della resistenza, il circuito CR si comporta come filtro passa alto:

VC 
V oC

1
V in
1  j  RC
V oin

2
1   
  arctan  

VR 
V oR 

j  RC 
V in
1  j  RC
 V oin
1  
2
  arctan 1 / 

Seconda esperienza (12 Aprile 2017) • Carica e scarica di un condensatore (con costante di tempo breve).
• Uso dell’ oscilloscopio. • Studio del circuito RC (onda quadra) e CR (onda quadra)
• Avrete a disposizione:
–
–
–
–
–
–
–
Condensatori
Resistenze
Cronometro
Multimetro digitale
Cavi di collegamento
Oscilloscopio iso‐tech isr 622 a 2 canali
Generatore di segnali alternati (sinusoidali, quadri etc.)
Prima parte esercitazione 2 : carica e scarica del condensatore (circuito RC con breve costante di tempo)
• Sostituire R e C con valori inferiori (2.7k e 22nF). La costante di tempo è molto diminuita (RC=59s) e il processo è troppo veloce per usare voltmetro e cronometro.
• Però si può visualizzare lo stesso il processo di carica (e scarica) usando l’oscilloscopio. • Invece che caricare e scaricare il condensatore collegandolo a mano all’alimentatore Vo, si usa un generatore di funzioni che può generare tensioni periodiche di diverse forme. • L’ uscita TTL genera una tensione periodica che si alterna tra 0V e 5V. • Usando un periodo molto più lungo della costante di tempo, quando la tensione transisce da 0 a 5V inizia la carica del condensatore, che si completa prima che la tensione transisca nuovamente a 0V.
• Quando transisce da 5V a 0V parte la scarica. Anche questa si completa prima della successiva transizione del generatore da 0V a 5V.
Prima parte esercitazione 2 : carica e scarica del condensatore (circuito RC con breve costante di tempo)
Circuito
RC
Vg(t)=0V..5V
Vg(t)
Generatore di
funzioni
(uscita TTL,
frequenza
f=1kHz)
5V
0V
C
Vc(t)
Resistenza
interna R2
500s
500s
0V
Vc
oscilloscopio
f=1/T=1.0 kHz
Vg
5V
R1
60s
60s
t
t
Generatore di funzioni
Regolazione frequenza
Uscita TTL del generatore di funzioni Prima parte esercitazione 2 : (circuito RC con breve costante di tempo)
•
•
•
•
Scegliendo un periodo dell’onda quadra di 1 ms (frequenza 1 kHz) si ha abbastanza tempo nella fase alta e nella fase bassa della tensione del generatore per consentire la carica e scarica praticamente complete del condensatore.
Sullo schermo si possono quindi campionare i valori della tensione al passare del tempo, e ricostruire lo stesso grafico fatto nella prima parte dell’esperienza, dal quale si misurerà nello stesso modo la nuova costante di tempo. Si possono usare anche i dati della scarica, con la formula relativa, e la costante di tempo deve venire la stessa entro gli errori.
La resistenza interna dell’oscilloscopio è molto elevata (1M) e quindi non è facilmente misurabile in questo caso. 100 s/cm
5
1V/cm
Vc(V)
VC (t )  VE e(t to ) /
VC (t )  VE (1  e t / )
t(s)
0
0
500
1000
Seconda parte esercitazione 2 : (circuito RC con breve costante di tempo con partitore)
• Si aggiunge un resistore in parallelo al condensatore (ad es.da 2.7k).
• Si ripetono le misure di tensione ai capi del condensatore in funzione del tempo. Che differenze ci sono rispetto al caso precedente ?
• Quale è il valore asintotico per la tensione di carica del condensatore?
• Come cambia la costante di tempo? Perché? (vedi lezioni)
Vg(t)
Generatore di
funzioni
(uscita TTL,
frequenza
f=1kHz)
Vg(t)=0V..5V
Circuito
RC
R1
oscilloscopio
R2
C
Vc(t)
Resistenza
interna
Circuito RC : schema di montaggio
R
C
Generatore Oscilloscopio
di segnali CH 1: misura Vin
=coccodrilli rossi
Basetta
Oscilloscopio
CH2: misura Vout
=coccodrilli neri
• Problemi pratici:
• Le connessioni ai BNC vanno fatte con cavetti BNC‐coccodrillo. Il rosso è connesso al centrale, il nero allo schermo.
CH1
CH2
Oscilloscopio
R
GEN
C
Generatore
di segnali
Basetta
Oscilloscopio
Terza parte esercitazione 2 : (circuito CR con breve costante di tempo)
• Scambiando R con C nel circuito della parte 1 dell’esperienza, e prendendo il segnale ai capi di R, si misuri, con l’onda quadra in ingresso, la tensione in funzione del tempo.
• Si verifichi che il valore della costante di tempo è entro gli errori, compatibile con quella ricavata nella parte 1 dell’esperienza.
• Confrontare con il valore ottenuto a partire dalla misura di R e C con il ponte
Circuito CR : schema di montaggio
C
R
Generatore Oscilloscopio
di segnali CH 1: misura Vin
=coccodrilli rossi
Basetta
Oscilloscopio
CH2: misura Vout
=coccodrilli neri
• Problemi pratici:
• Le connessioni ai BNC vanno fatte con cavetti BNC‐coccodrillo. Il rosso e’ connesso al centrale, il nero allo schermo.
T CH1
CH2
Oscilloscopio
C
GEN
R
Generatore
di segnali
Basetta
Oscilloscopio
Terza parte esercitazione 2 : (circuito CR con breve costante di tempo)
•
Scegliendo un periodo dell’onda quadra di 1 ms (frequenza 1 kHz) si ha abbastanza tempo nella fase alta e nella fase bassa della tensione del generatore per consentire la carica e scarica praticamente complete del condensatore.
100 s/cm
VR(V)
5
1V/cm
VR (t )  VE et /
t(s)
0
0
500
1000
VR (t )  VE e  (t to ) /