MATEMATICA GENERALE
prof. Mauro Pagliacci
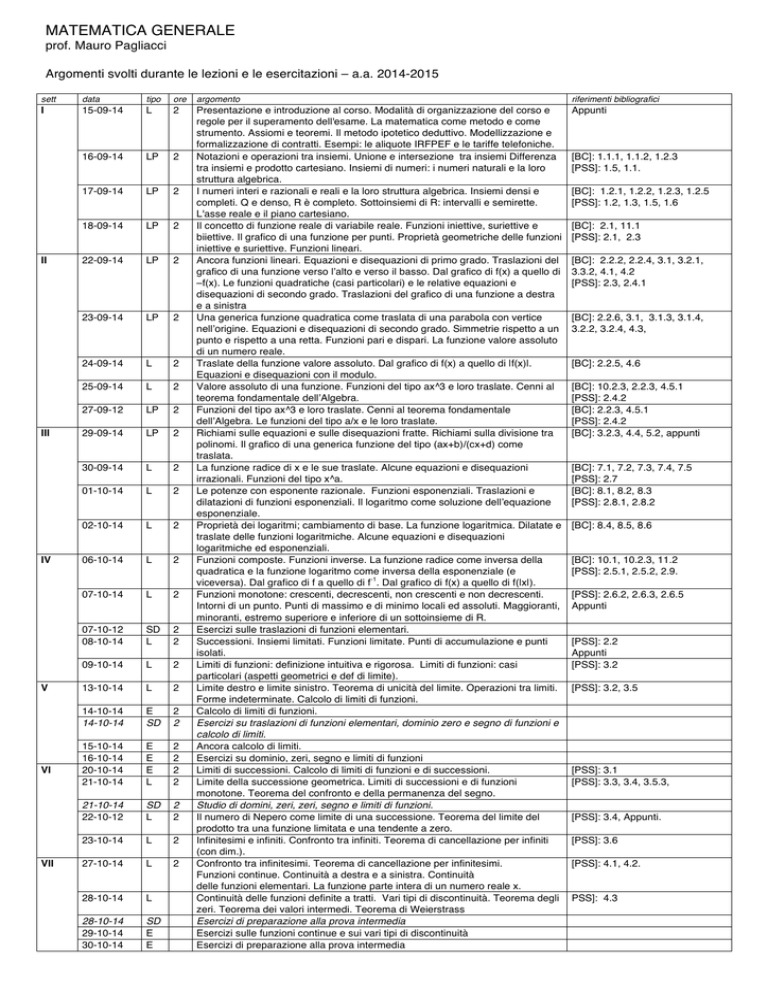
Argomenti svolti durante le lezioni e le esercitazioni – a.a. 2014-2015
sett
data
tipo
ore
argomento
riferimenti bibliografici
I
15-09-14
L
2
Appunti
16-09-14
LP
2
17-09-14
LP
2
18-09-14
LP
2
22-09-14
LP
2
23-09-14
LP
2
24-09-14
L
2
25-09-14
L
2
27-09-12
LP
2
29-09-14
LP
2
30-09-14
L
2
01-10-14
L
2
02-10-14
L
2
06-10-14
L
2
07-10-14
L
2
07-10-12
08-10-14
SD
L
2
2
09-10-14
L
2
13-10-14
L
2
14-10-14
14-10-14
E
SD
2
2
15-10-14
16-10-14
20-10-14
21-10-14
E
E
E
L
2
2
2
2
21-10-14
22-10-12
SD
L
2
2
23-10-14
L
2
27-10-14
L
2
28-10-14
L
28-10-14
29-10-14
30-10-14
SD
E
E
Presentazione e introduzione al corso. Modalità di organizzazione del corso e
regole per il superamento dell'esame. La matematica come metodo e come
strumento. Assiomi e teoremi. Il metodo ipotetico deduttivo. Modellizzazione e
formalizzazione di contratti. Esempi: le aliquote IRFPEF e le tariffe telefoniche.
Notazioni e operazioni tra insiemi. Unione e intersezione tra insiemi Differenza
tra insiemi e prodotto cartesiano. Insiemi di numeri: i numeri naturali e la loro
struttura algebrica.
I numeri interi e razionali e reali e la loro struttura algebrica. Insiemi densi e
completi. Q e denso, R è completo. Sottoinsiemi di R: intervalli e semirette.
L'asse reale e il piano cartesiano.
Il concetto di funzione reale di variabile reale. Funzioni iniettive, suriettive e
biiettive. Il grafico di una funzione per punti. Proprietà geometriche delle funzioni
iniettive e suriettive. Funzioni lineari.
Ancora funzioni lineari. Equazioni e disequazioni di primo grado. Traslazioni del
grafico di una funzione verso l’alto e verso il basso. Dal grafico di f(x) a quello di
–f(x). Le funzioni quadratiche (casi particolari) e le relative equazioni e
disequazioni di secondo grado. Traslazioni del grafico di una funzione a destra
e a sinistra
Una generica funzione quadratica come traslata di una parabola con vertice
nell’origine. Equazioni e disequazioni di secondo grado. Simmetrie rispetto a un
punto e rispetto a una retta. Funzioni pari e dispari. La funzione valore assoluto
di un numero reale.
Traslate della funzione valore assoluto. Dal grafico di f(x) a quello di |f(x)|.
Equazioni e disequazioni con il modulo.
Valore assoluto di una funzione. Funzioni del tipo ax^3 e loro traslate. Cenni al
teorema fondamentale dell’Algebra.
Funzioni del tipo ax^3 e loro traslate. Cenni al teorema fondamentale
dell’Algebra. Le funzioni del tipo a/x e le loro traslate.
Richiami sulle equazioni e sulle disequazioni fratte. Richiami sulla divisione tra
polinomi. Il grafico di una generica funzione del tipo (ax+b)/(cx+d) come
traslata.
La funzione radice di x e le sue traslate. Alcune equazioni e disequazioni
irrazionali. Funzioni del tipo x^a.
Le potenze con esponente razionale. Funzioni esponenziali. Traslazioni e
dilatazioni di funzioni esponenziali. Il logaritmo come soluzione dell’equazione
esponenziale.
Proprietà dei logaritmi; cambiamento di base. La funzione logaritmica. Dilatate e
traslate delle funzioni logaritmiche. Alcune equazioni e disequazioni
logaritmiche ed esponenziali.
Funzioni composte. Funzioni inverse. La funzione radice come inversa della
quadratica e la funzione logaritmo come inversa della esponenziale (e
-1
viceversa). Dal grafico di f a quello di f . Dal grafico di f(x) a quello di f(|x|).
Funzioni monotone: crescenti, decrescenti, non crescenti e non decrescenti.
Intorni di un punto. Punti di massimo e di minimo locali ed assoluti. Maggioranti,
minoranti, estremo superiore e inferiore di un sottoinsieme di R.
Esercizi sulle traslazioni di funzioni elementari.
Successioni. Insiemi limitati. Funzioni limitate. Punti di accumulazione e punti
isolati.
Limiti di funzioni: definizione intuitiva e rigorosa. Limiti di funzioni: casi
particolari (aspetti geometrici e def di limite).
Limite destro e limite sinistro. Teorema di unicità del limite. Operazioni tra limiti.
Forme indeterminate. Calcolo di limiti di funzioni.
Calcolo di limiti di funzioni.
Esercizi su traslazioni di funzioni elementari, dominio zero e segno di funzioni e
calcolo di limiti.
Ancora calcolo di limiti.
Esercizi su dominio, zeri, segno e limiti di funzioni
Limiti di successioni. Calcolo di limiti di funzioni e di successioni.
Limite della successione geometrica. Limiti di successioni e di funzioni
monotone. Teorema del confronto e della permanenza del segno.
Studio di domini, zeri, zeri, segno e limiti di funzioni.
Il numero di Nepero come limite di una successione. Teorema del limite del
prodotto tra una funzione limitata e una tendente a zero.
Infinitesimi e infiniti. Confronto tra infiniti. Teorema di cancellazione per infiniti
(con dim.).
Confronto tra infinitesimi. Teorema di cancellazione per infinitesimi.
Funzioni continue. Continuità a destra e a sinistra. Continuità
delle funzioni elementari. La funzione parte intera di un numero reale x.
Continuità delle funzioni definite a tratti. Vari tipi di discontinuità. Teorema degli
zeri. Teorema dei valori intermedi. Teorema di Weierstrass
Esercizi di preparazione alla prova intermedia
Esercizi sulle funzioni continue e sui vari tipi di discontinuità
Esercizi di preparazione alla prova intermedia
II
III
IV
V
VI
VII
[BC]: 1.1.1, 1.1.2, 1.2.3
[PSS]: 1.5, 1.1.
[BC]: 1.2.1, 1.2.2, 1.2.3, 1.2.5
[PSS]: 1.2, 1.3, 1.5, 1.6
[BC]: 2.1, 11.1
[PSS]: 2.1, 2.3
[BC]: 2.2.2, 2.2.4, 3.1, 3.2.1,
3.3.2, 4.1, 4.2
[PSS]: 2.3, 2.4.1
[BC]: 2.2.6, 3.1, 3.1.3, 3.1.4,
3.2.2, 3.2.4, 4.3,
[BC]: 2.2.5, 4.6
[BC]: 10.2.3, 2.2.3, 4.5.1
[PSS]: 2.4.2
[BC]: 2.2.3, 4.5.1
[PSS]: 2.4.2
[BC]: 3.2.3, 4.4, 5.2, appunti
[BC]: 7.1, 7.2, 7.3, 7.4, 7.5
[PSS]: 2.7
[BC]: 8.1, 8.2, 8.3
[PSS]: 2.8.1, 2.8.2
[BC]: 8.4, 8.5, 8.6
[BC]: 10.1, 10.2.3, 11.2
[PSS]: 2.5.1, 2.5.2, 2.9.
[PSS]: 2.6.2, 2.6.3, 2.6.5
Appunti
[PSS]: 2.2
Appunti
[PSS]: 3.2
[PSS]: 3.2, 3.5
[PSS]: 3.1
[PSS]: 3.3, 3.4, 3.5.3,
[PSS]: 3.4, Appunti.
[PSS]: 3.6
[PSS]: 4.1, 4.2.
PSS]: 4.3
VIII
IX
X
XI
XII
XIII
10-11-14
L
2
11-11-14
L
2
12-11-14
L
2
13-11-14
L
2
17-11-14
L
2
18-11-14
L
2
18-11-14
19-11-14
SD
L
2
2
20-11-14
L
2
24-11-14
L
2
25-11-14
L
2
26-11-14
L
2
27-11-14
27-11-14
01-12-14
E
SD
L
2
2
2
02-12-14
L
2
03-12-14
L
2
04-12-14
L
2
04-12-14
05-12-14
SD
L
2
2
09-12-14
10-12-14
SD
2
11-12-14
L
2
11-12-14
L
2
12-12-14
L
2
15-12-14
L
2
16-12-14
17-12-14
18-12-14
SD
L
L+
E
E
E
2
2
2
18-12-14
19-12-14
Legenda
tipo
riferimenti bibliografici
2
2
Incrementi assoluti e relativi. Rapporto incrementale. Significato geometrico del [PSS]: 5.1 (parte)
rapporto incrementale. Funzioni derivabili in un punto. Derivata prima.
Significato geometrico della derivata prima. Derivata destra e sinistra. La
[PSS]: 5.1 (completare), 5.2, 5.3.
funzione derivata prima. Ogni funzione derivabile è continua (con dim.). Vari
casi di funzioni continue, ma non derivabili. Calcolo di derivate di funzioni
elementari.
Calcolo di derivate di funzioni elementari e algebra delle derivate. Derivate delle [PSS]: 5.3, 5.4.1
funzioni composte.
Calcolo di derivate. Funzioni differenziabili. Equivalenza tra differenziabilità e
[PSS]: 5.5
derivabilità (con dim.).
Il differenziale e il suo significato geometrico. Uso del differenziale nel calcolo
[PSS]: 5.5, Appunti.
approssimato.
Elasticità d’arco ed elasticità puntuale. Elasticità della funzione domanda e della [PSS]: 5.6.1, 5.7.
funzione costo. Introduzione all’ottimizzazione. Teorema di Fermat (con dim.).
Esercizi sul calcolo di derivate e sul differenziale
Teorema di Lagrange (o del valor medio). Conseguenze del teorema di
[PSS]: 5.8, 5.9
Lagrange. Il teorema di Rolle. Ogni funzione con derivata nulla è costante (con
dim.). Test di monotonia (con dim.).
Determinazione dei punti di massimo e di minimo. Esempio di studio della
[PSS]: 5..9, 5.10.
monotonia e di massimi e minimi locali e assoluti. Teorema di de l’Hospital.
[PSS]: 5.11,
Appunti.
Ordine di infinito e di infinitesimo dell’esponenziale e del logaritmo. Derivate successive.
Formula
di
[PSS]: 5.10, 5.11,
Taylor e di Mc Laurin. Uso della formula di Taylor nel calcolo approssimato.
Grafico di e^x e dei polinomi di Taylor che la approssimano. Primitive di una
[PSS]: 7.5.1, 7.5.2.
funzione. Due primitive di una stessa funzione differiscono per una costante
(con dim.). Integrale indefinito. Calcolo di integrali indefiniti immediati.
Integrazione per decomposizione. Integrazione per sostituzione. Integrazione
[PSS]: 7.5.4, 7.5.3.
per parti. Calcolo di integrali indefiniti.
Calcolo di integrali indefiniti. Integrale definito. Funzioni integrabili.
[PSS]: 7.1, 7.2
Esercizi sullo studio di funzione e sugli integrali
Proprietà dell’integrale definito. Teorema della media (con dim.). Funzione
[PSS]: 7.3.1, 7.3
integrale.
Teorema di Torricelli Barrow (con dim.) e Teorema fondamentale del calcolo
[PSS]: 7.4, 7.9
integrale (con dim.). Calcolo di integrali definiti. Calcolo di aree
Introduzione all’algebra lineare. Vettori in R^n. Rappresentazione geometrica di
vettori in R^2 e in R^3. Uguaglianza e somma tra vettori.
[PSS]: 8.1.
Significato geometrico della somma tra vettori. Moltiplicazione di un vettore per
[PSS]: 8.2, 8.3.
uno scalare e suo significato geometrico. Combinazioni lineari. Prodotto scalare
tra vettori. Sottospazi vettoriali.
Eercizi sullo studio di funzione e sugli integrali
Sottospazi vettoriali di R^2 e R^3. L’insieme delle combinazioni lineari di k
[PSS]: 8.4, 8.5
vettori è un sottospazio di R^n. Dipendenza e indipendenza lineare
Esercizi su studio di funzioni e integrali
Basi e dimensioni di un sottospazio. Matrici. Uguaglianza, matrici trasposte,
[PSS]: 8.6, 8.7.
simmetriche, triangolari e diagonali.
Operazioni tra matrici: somma e prodotto per uno scalare. Prodotto tra matrici.
[PSS]: 8.8.1, 8.8.2, 8.9
Proprietà del prodotto. Determinante di una matrice quadrata 2x2 e suo
significato geometrico. Relazione tra dipendenza lineare e determinante.
Determinante di una matrice 3x3. Cenno al teorema di Laplace. Calcolo del
[PSS]: 8.9, 8.11.
determinante con Excel. Rango di una matrice.
Sistemi lineari. Teorema di Rouché-Capelli (con dim.). Regola di Cramer.
[PSS]: 9.1, 9.2, 9.3.
Risoluzione di un sistema lineare.
Molteplicità delle soluzioni di un sistema lineare. Sistemi lineari omogenei.
[PSS]: 9.4
Esercizi sui sistemi e sui vettori linearmente dip/indip.
Esercizi su integrali e studio di funzioni
Funzioni di più variabili. Grafico e curve di livello. Derivate parziali.
[PSS]: 10.1, 10.2, 10.3, 10.6.
Massimi e minimi assoluti e vincolati per funzioni di due variabili.
[PSS]: 10.11 (parte), 10.12
Esercizi di algebra lineare.
(parte).
Esercizi di algebra lineare.
Esercizi di preparazione alla prova scritta.
LP: lezione propedeutica, L: lezione, .E: esercitazione, SD: attività di supporto alla didattica.
[BC]: Boieri, Chiti – Precorso di Matematica, Zanichelli
[PSS]:Peccati, Salsa, Squellati – Matematica per l’economia e l’azienda, Egea (2004)
nota: [PSS]: 2.1 significa capitolo 2, paragrafo 1 del testo [PSS].
[PSS]: 2.1.2 significa capitolo 2, paragrafo 1, sottoparagrafo 2 del testo [PSS].