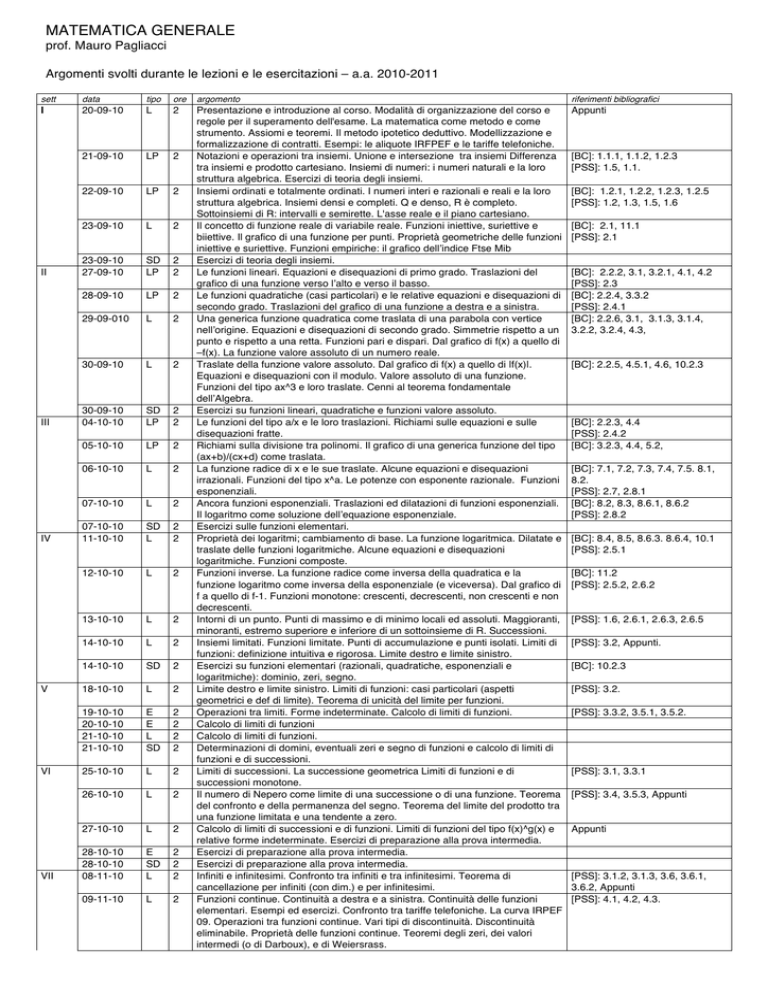
MATEMATICA GENERALE
prof. Mauro Pagliacci
Argomenti svolti durante le lezioni e le esercitazioni – a.a. 2010-2011
sett
data
tipo
ore
argomento
riferimenti bibliografici
I
20-09-10
L
2
Appunti
21-09-10
LP
2
22-09-10
LP
2
23-09-10
L
2
23-09-10
27-09-10
SD
LP
2
2
28-09-10
LP
2
29-09-010
L
2
30-09-10
L
2
30-09-10
04-10-10
SD
LP
2
2
05-10-10
LP
2
06-10-10
L
2
07-10-10
L
2
07-10-10
11-10-10
SD
L
2
2
12-10-10
L
2
13-10-10
L
2
14-10-10
L
2
14-10-10
SD
2
18-10-10
L
2
19-10-10
20-10-10
21-10-10
21-10-10
E
E
L
SD
2
2
2
2
25-10-10
L
2
26-10-10
L
2
27-10-10
L
2
28-10-10
28-10-10
08-11-10
E
SD
L
2
2
2
09-11-10
L
2
Presentazione e introduzione al corso. Modalità di organizzazione del corso e
regole per il superamento dell'esame. La matematica come metodo e come
strumento. Assiomi e teoremi. Il metodo ipotetico deduttivo. Modellizzazione e
formalizzazione di contratti. Esempi: le aliquote IRFPEF e le tariffe telefoniche.
Notazioni e operazioni tra insiemi. Unione e intersezione tra insiemi Differenza
tra insiemi e prodotto cartesiano. Insiemi di numeri: i numeri naturali e la loro
struttura algebrica. Esercizi di teoria degli insiemi.
Insiemi ordinati e totalmente ordinati. I numeri interi e razionali e reali e la loro
struttura algebrica. Insiemi densi e completi. Q e denso, R è completo.
Sottoinsiemi di R: intervalli e semirette. L'asse reale e il piano cartesiano.
Il concetto di funzione reale di variabile reale. Funzioni iniettive, suriettive e
biiettive. Il grafico di una funzione per punti. Proprietà geometriche delle funzioni
iniettive e suriettive. Funzioni empiriche: il grafico dell’indice Ftse Mib
Esercizi di teoria degli insiemi.
Le funzioni lineari. Equazioni e disequazioni di primo grado. Traslazioni del
grafico di una funzione verso l’alto e verso il basso.
Le funzioni quadratiche (casi particolari) e le relative equazioni e disequazioni di
secondo grado. Traslazioni del grafico di una funzione a destra e a sinistra.
Una generica funzione quadratica come traslata di una parabola con vertice
nell’origine. Equazioni e disequazioni di secondo grado. Simmetrie rispetto a un
punto e rispetto a una retta. Funzioni pari e dispari. Dal grafico di f(x) a quello di
–f(x). La funzione valore assoluto di un numero reale.
Traslate della funzione valore assoluto. Dal grafico di f(x) a quello di |f(x)|.
Equazioni e disequazioni con il modulo. Valore assoluto di una funzione.
Funzioni del tipo ax^3 e loro traslate. Cenni al teorema fondamentale
dell’Algebra.
Esercizi su funzioni lineari, quadratiche e funzioni valore assoluto.
Le funzioni del tipo a/x e le loro traslazioni. Richiami sulle equazioni e sulle
disequazioni fratte.
Richiami sulla divisione tra polinomi. Il grafico di una generica funzione del tipo
(ax+b)/(cx+d) come traslata.
La funzione radice di x e le sue traslate. Alcune equazioni e disequazioni
irrazionali. Funzioni del tipo x^a. Le potenze con esponente razionale. Funzioni
esponenziali.
Ancora funzioni esponenziali. Traslazioni ed dilatazioni di funzioni esponenziali.
Il logaritmo come soluzione dell’equazione esponenziale.
Esercizi sulle funzioni elementari.
Proprietà dei logaritmi; cambiamento di base. La funzione logaritmica. Dilatate e
traslate delle funzioni logaritmiche. Alcune equazioni e disequazioni
logaritmiche. Funzioni composte.
Funzioni inverse. La funzione radice come inversa della quadratica e la
funzione logaritmo come inversa della esponenziale (e viceversa). Dal grafico di
f a quello di f-1. Funzioni monotone: crescenti, decrescenti, non crescenti e non
decrescenti.
Intorni di un punto. Punti di massimo e di minimo locali ed assoluti. Maggioranti,
minoranti, estremo superiore e inferiore di un sottoinsieme di R. Successioni.
Insiemi limitati. Funzioni limitate. Punti di accumulazione e punti isolati. Limiti di
funzioni: definizione intuitiva e rigorosa. Limite destro e limite sinistro.
Esercizi su funzioni elementari (razionali, quadratiche, esponenziali e
logaritmiche): dominio, zeri, segno.
Limite destro e limite sinistro. Limiti di funzioni: casi particolari (aspetti
geometrici e def di limite). Teorema di unicità del limite per funzioni.
Operazioni tra limiti. Forme indeterminate. Calcolo di limiti di funzioni.
Calcolo di limiti di funzioni
Calcolo di limiti di funzioni.
Determinazioni di domini, eventuali zeri e segno di funzioni e calcolo di limiti di
funzioni e di successioni.
Limiti di successioni. La successione geometrica Limiti di funzioni e di
successioni monotone.
Il numero di Nepero come limite di una successione o di una funzione. Teorema
del confronto e della permanenza del segno. Teorema del limite del prodotto tra
una funzione limitata e una tendente a zero.
Calcolo di limiti di successioni e di funzioni. Limiti di funzioni del tipo f(x)^g(x) e
relative forme indeterminate. Esercizi di preparazione alla prova intermedia.
Esercizi di preparazione alla prova intermedia.
Esercizi di preparazione alla prova intermedia.
Infiniti e infinitesimi. Confronto tra infiniti e tra infinitesimi. Teorema di
cancellazione per infiniti (con dim.) e per infinitesimi.
Funzioni continue. Continuità a destra e a sinistra. Continuità delle funzioni
elementari. Esempi ed esercizi. Confronto tra tariffe telefoniche. La curva IRPEF
09. Operazioni tra funzioni continue. Vari tipi di discontinuità. Discontinuità
eliminabile. Proprietà delle funzioni continue. Teoremi degli zeri, dei valori
intermedi (o di Darboux), e di Weiersrass.
II
III
IV
V
VI
VII
[BC]: 1.1.1, 1.1.2, 1.2.3
[PSS]: 1.5, 1.1.
[BC]: 1.2.1, 1.2.2, 1.2.3, 1.2.5
[PSS]: 1.2, 1.3, 1.5, 1.6
[BC]: 2.1, 11.1
[PSS]: 2.1
[BC]: 2.2.2, 3.1, 3.2.1, 4.1, 4.2
[PSS]: 2.3
[BC]: 2.2.4, 3.3.2
[PSS]: 2.4.1
[BC]: 2.2.6, 3.1, 3.1.3, 3.1.4,
3.2.2, 3.2.4, 4.3,
[BC]: 2.2.5, 4.5.1, 4.6, 10.2.3
[BC]: 2.2.3, 4.4
[PSS]: 2.4.2
[BC]: 3.2.3, 4.4, 5.2,
[BC]: 7.1, 7.2, 7.3, 7.4, 7.5. 8.1,
8.2.
[PSS]: 2.7, 2.8.1
[BC]: 8.2, 8.3, 8.6.1, 8.6.2
[PSS]: 2.8.2
[BC]: 8.4, 8.5, 8.6.3. 8.6.4, 10.1
[PSS]: 2.5.1
[BC]: 11.2
[PSS]: 2.5.2, 2.6.2
[PSS]: 1.6, 2.6.1, 2.6.3, 2.6.5
[PSS]: 3.2, Appunti.
[BC]: 10.2.3
[PSS]: 3.2.
[PSS]: 3.3.2, 3.5.1, 3.5.2.
[PSS]: 3.1, 3.3.1
[PSS]: 3.4, 3.5.3, Appunti
Appunti
[PSS]: 3.1.2, 3.1.3, 3.6, 3.6.1,
3.6.2, Appunti
[PSS]: 4.1, 4.2, 4.3.
VIII
IX
X
XI
XII
10-11-10
L
1
11-11-10
L
2
11-11-10
15-11-10
16-11-10
SD
L
E
2
2
2
17-11-10
L
2
18-11-10
L
2
18-11-10
SD
2
22-11-10
L
2
23-11-10
L
2
24-11-10
L
2
25-11-10
25-11-10
29-11-10
L
SD
L
2
2
2
30-11-10
01-12-10
E
L
2
2
02-12-10
L
2
02-12-10
03-12-10
06-12-10
SD
E
L
2
2
2
07-12-10
L
2
09-12-10
L
2
09-12-10
10-12-10
SD
L
2
2
13-12-10
L
14-12-10
L
15-12-10
L
16-12-10
L
Invertibilità e continuità.
Incrementi assoluti e relativi. Rapporto incrementale. Significato geometrico del
rapporto incrementale. Funzioni derivabili in un punto. Derivata prima.
Significato geometrico della derivata prima. Derivata destra e sinistra. La
funzione derivata prima. Ogni funzione derivabile è continua (con dim.). Vari
casi di funzioni continue, ma non derivabili.
Esercizi sulle funzioni continue. Calcolo di derivate di funzioni elementari.
Ancora calcolo di derivate di funzioni elementari. Algebra delle derivate.
Derivate delle funzioni composte. Calcolo di derivate. Derivabilità della funzione
che rappresenta l’IRPEF. Aliquote marginali.
Funzione costo di produzione. Costo marginale. Funzioni differenziabili.
Equivalenza tra differenziabilità e derivabilità (con dim.). Il differenziale e il suo
significato geometrico. Uso del differenziale nel calcolo approssimato.
Ancora uso del differenziale nel calcolo approssimato. Elasticità d’arco ed
elasticità puntuale. Elasticità della funzione domanda e della funzione costo.
Introduzione all’ottimizzazione. Teorema di Fermat (con dim.) e teorema di
Lagrange (o del valor medio).
Esercizi sul calcolo di derivate e sull’uso del differenziale nel calcolo
approssimato.
Conseguenze del teorema di Lagrange. Il teorema di Rolle. Ogni funzione con
derivata nulla è costante (con dim.). Test di monotonia (con dim.).
Determinazione dei punti di massimo e di minimo.
Esempi di studio della monotonia e di massimi e minimi locali e assoluti.
Teorema di de l’Hospital. Ordine di infinito dell’esponenziale.
Ordine di infinito del logaritmo. Derivate successive. Formula di Taylor e di Mc
Laurin. Uso della formula di Taylor nel calcolo approssimato.
Insiemi convessi e funzioni convesse. Funzioni concave. Test per la convessità
Esercizi sullo studio dei massimi e minimi, sulla convessità.
Primitive di una funzione. Due primitive di una stessa funzione differiscono per
una costante (con dim.). Integrale indefinito. Calcolo di integrali indefiniti
immediati. Integrazione per decomposizione. Integrazione per sostituzione.
Integrazione per parti. Calcolo di integrali indefiniti.
Integrale definito. Funzioni integrabili. Proprietà dell’integrale definito. Teorema
della media (con dim.). Funzione integrale. Teorema di Torricelli-Barrow.
Dimostrazione del teorema di Torricelli Barrow. Teorema fondamentale del
calcolo integrale (con dim.). Calcolo di integrali definiti e di aree.
Esercizi sullo studio di funzioni.
Esercizi sul calcolo di integrali definiti, indefiniti e di aree.
Introduzione all’algebra lineare. Vettori. Uguaglianza e ordinamento tra vettori.
Somma tra vettori e prodotto per uno scalare. Significato geometrico della
somma tra vettori.
Significato geometrico del prodotto tra un numero e un vettore. Combinazioni
lineari. Prodotto scalare tra vettori. Sottospazi vettoriali.
Sottospazi vettoriali di R^2 e R^3. L’insieme delle combinazioni lineari di k
vettori è un sottospazio di R^n (con dim.). Dipendenza e indipendenza lineare.
Esercizi su studio di funzioni e calcolo di integrali.
Basi e dimensioni di un sottospazio. Matrici. Uguaglianza, matrici trasposte,
simmetriche, triangolari e diagonali. Operazioni tra matrici: somma e prodotto
per uno scalare.
Prodotto tra matrici. Proprietà del prodotto. Determinante di una matrice
quadrata 2x2 e suo significato geometrico. Relazione tra dipendenza lineare e
determinante.
Determinante di una matrice 3x3. Cenno al teorema di Laplace. Calcolo del
determinante con Excel. Rango di una matrice.
Ancora sul rango di una matrice. Sistemi lineari. Teorema di Rouché-Capelli
(con dim.). Regola di Cramer.
Molteplicità delle soluzioni. Sistemi omogenei.
Cenni sulle funzioni di più variabili. Grafico di una funzione in due variabili.
Curve di livello. Derivate parziali.
Esercizi di algebra lineare.
Esercizi di algebra lineare.
[PSS]: 4.3 (completare), 5.1
(parte)
[PSS]: 5.1 (completare), 5.2
[PSS]: 5.2, 5.3.
[PSS]: 5.4.1.
Appunti
[PSS]: 5.5
[PSS]: 5.6.1, 5.7, 5.8 (parte).
[PSS]: 5.8 (completare), 5.9.
[PSS]: 5.10, appunti.
[PSS]: appunti, 5.11.
[PSS]: 2.6.4, 5.12.
[PSS]: 7.5.1, 7.5.2, 7.5.4.
[PSS]: 7.5.4, 7.5.3.
[PSS]: 7.1, 7.2, 7.3, 7.9.
[PSS]: 7.9, 7.4.
[PSS]: 8.1, 8.2 (parte).
[PSS]: 8.2 (completare), 8.3, 8.4
[PSS]: 8.4, 8.5
[PSS]: 8.6, 8.7, 8.8.1.
[PSS]: 8.8.2, 8.9 (parte).
[PSS]: 8.9 (completare), 8.11.
[PSS]: 9.1, 9.2, 9.3.
[PSS]: 9.4, 10.1, 10.2, 10.6.
16-12-10
E
17-12-10
SD
Legenda
tipo
LP: lezione propedeutica, L: lezione, .E: esercitazione, SD: attività di supporto alla didattica.
riferimenti bibliografici
[BC]: Boieri, Chiti – Precorso di Matematica, Zanichelli
[PSS]:Peccati, Salsa, Squellati – Matematica per l’economia e l’azienda, Egea (2004)
nota: [PSS]: 2.1 significa capitolo 2, paragrafo 1 del testo [PSS].
[PSS]: 2.1.2 significa capitolo 2, paragrafo 1, sottoparagrafo 2 del testo [PSS].