27/10/2016
RADIAZIONE ELETTROMAGNETICA (EM)
È una forma di trasmissione di energia attraverso il vuoto o un
mezzo, in cui il campo elettrico e il campo magnetico si propagano
sotto forma di ONDE
Onda = perturbazione che si propaga in un mezzo
(ma la radiazione EM può propagarsi anche nel vuoto)
Per una qualsiasi onda possiamo definire:
Ampiezza A (altezza massima sopra la linea media)
Lunghezza d’onda l (distanza tra due massimi consecutivi)
Frequenza n (il n. di massimi nell’unità di tempo)
1
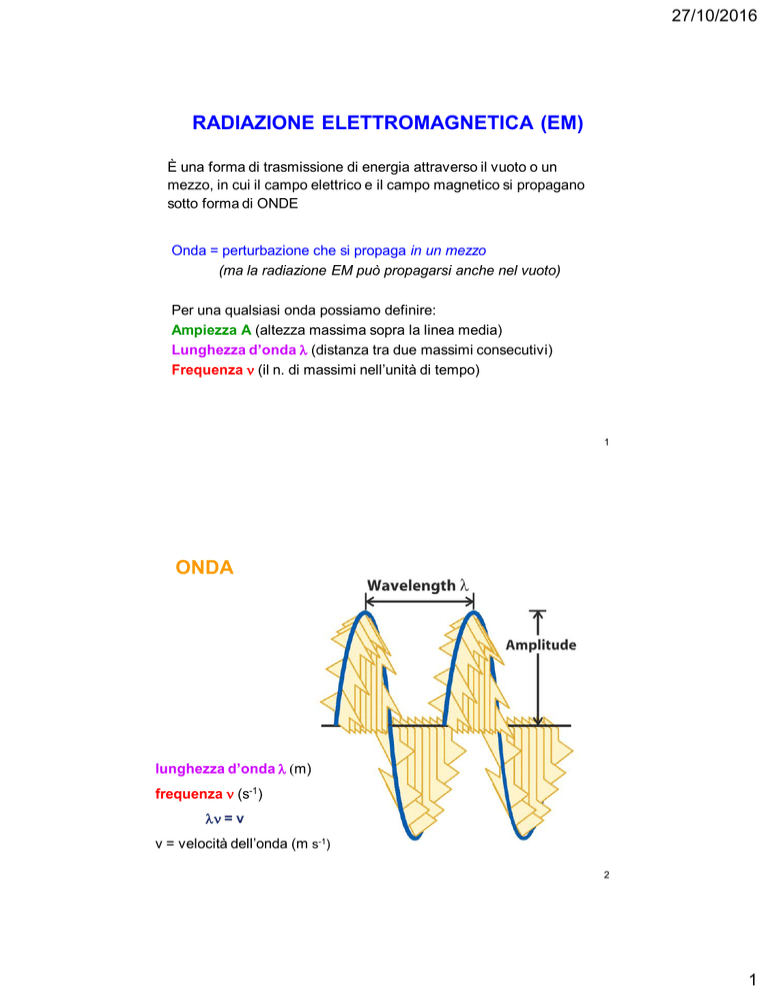
ONDA
lunghezza d’onda l (m)
frequenza n (s-1)
ln = v
v = velocità dell’onda (m s-1)
2
1
27/10/2016
Maggiore è la lunghezza d’onda, minore è la frequenza
3
RADIAZIONE ELETTROMAGNETICA (EM)
In una radiazione EM, la componente della radiazione associata al
campo elettrico oscilla su un piano perpendicolare a quello della
componente associata al campo magnetico.
Per una data radiazione EM, le lunghezze d’onda, frequenze e
ampiezze di campo elettrico e magnetico sono identici.
La velocità di propagazione nel vuoto di una radiazione EM è :
c= ln
dove c = 3.00 x 108 m/s
4
2
27/10/2016
TIPI COMUNI
di
RADIAZIONE
EM
5
Postulato di Planck: verso la meccanica quantistica
Inapplicabilità della fisica classica alle particelle piccolissime
Errore della fisica classica: ammettere che un oggetto sia in grado di
possedere quantità arbitrarie di energia
1900 – la proposta di Max Planck:
l’energia (come la materia) non è continua energia quantizzata
Postulato di Planck: una radiazione EM di frequenza n è
assimilabile a un fascio di particelle (fotoni) ciascuna dotata di
energia pari a E = h n
(h = 6.63 x 10-34 J s costante di Planck)
La quantità di energia che un campione di materia può assorbire o
emettere è anch’essa quantizzata: gli scambi di energia
avvengono per quanti di energia.
6
3
27/10/2016
SPETTRO ATOMICO dell’IDROGENO
Dallo studio degli spettri atomici sono state ottenute le prime prove della
quantizzazione dell’energia.
Facendo passare una corrente elettrica attraverso un campione di H2 a
bassa pressione, si osserva che il campione emette luce.
La corrente elettrica
(i) scinde le molecole H2 formando atomi H
(ii) eccita gli atomi H a energie superiori a quella dello stato
fondamentale: gli atomi eccitati si liberano dell’energia eccedente
emettendo radiazione EM.
La radiazione EM emessa dagli atomi H è costituita da un certo numero di
componenti, dette righe spettrali.
La riga più intensa cade nel visibile (l = 656 nm) ma si ottengono righe
anche nell’infrarosso e nell’ultravioletto.
7
SPETTRO ATOMICO dell’IDROGENO
8
4
27/10/2016
SPETTRI ATOMICI
Ogni elemento possiede un proprio spettro di emissione a righe:
le righe caratteristiche nello spettro di emissione di un elemento
vengono utilizzate per identificare la presenza dell'elemento in un
campione, e per determinarne la quantità.
L’osservazione di righe spettrali distinte suggerisce che
nell’atomo l’elettrone possa avere solo certi valori di energia.
Nel 1913 Bohr, riunendo le idee quantistiche di Planck e Einstein,
fornì la prima spiegazione degli spettri a righe dell’atomo di
idrogeno.
9
ATOMO DI BOHR
Il modello atomico accettato dalla comunità scientifica fino a inizio 1900
non indicava il modo in cui gli elettroni sono disposti al di fuori del nucleo.
Nel 1913 Bohr risolse questo problema usando l'ipotesi
quantistica di Planck.
POSTULATI DI BOHR per l’atomo di idrogeno:
1) l'elettrone si muove in orbite circolari attorno al nucleo, secondo un
moto descritto dalla fisica classica;
2) l'elettrone possiede solo una serie fissa di orbite permesse, dette
STATI STAZIONARI: finche' un elettrone resta in una delle orbite
permesse la sua energia resta costante, e non si ha emissione di
energia;
3) un elettrone puo' passare solo da un'orbita permessa a un'altra. In
queste transizioni vengono coinvolte quantita' discrete di energia
(quanti di energia), in accordo con l'equazione di Planck E = h n.
10
5
27/10/2016
ATOMO DI BOHR
La teoria di Bohr consente di prevedere i raggi delle orbite permesse
in un atomo di idrogeno, i valori dei quali dipendono da un numero
intero positivo n che è chiamato numero quantico.
A ciascun valore di n corrisponde un valore permesso di energia:
l’energia dell’elettrone aumenta all’aumentare del valore di n
E’ possibile calcolare l’energia degli stati energetici permessi o
LIVELLI ENERGETICI dell’atomo di idrogeno.
11
BOHR: livelli energetici permessi
per l’atomo di idrogeno
Quando l’elettrone acquista un quanto di
energia, si sposta per es. dallo stato
fondamentale (n=1) a uno dei possibili stati
eccitati (per es. lo stato con n=2).
Nel ritornare allo stato fondamentale viene
emesso un fotone di energia pari a
DE21 = E2 – E1 = h n = E (fotone)
condizione della frequenza di Bohr
12
6
27/10/2016
ATOMO DI BOHR e
SPETTRI ATOMICI
DEn1 = En – E1 = h n = E (fotone)
Maggiore è la differenza di energia DE
tra i due livelli interessati dalla
transizione elettronica, maggiore sarà
la frequenza del fotone emesso.
Il modello di Bohr funziona bene per l’atomo di idrogeno e le specie idrogenoidi (He+, Li++)
ma NON è in grado di prevedere gli spettri atomici degli atomi polielettronici.
13
QUANTOMECCANICA
Sviluppata da Bohr e Schroedinger, è la teoria attualmente accettata
per descrivere il comportamento degli elettroni negli atomi.
PRESUPPOSTI :
1. Dualismo onda-particella (de Broglie)
a un elettrone libero di massa m, che si muove con velocita' v, e'
associata una lunghezza d'onda data dall'equazione:
l = h/(mv)
l'elettrone ha duplici proprieta', cioe' si comporta
simultaneamente sia come un'onda che come una particella.
In generale, a ogni oggetto in moto è associata una lunghezza
d’onda, che è misurabile solo per particelle con massa
estremamente piccola (= particelle subatomiche)
14
7
27/10/2016
QUANTOMECCANICA
PRESUPPOSTI :
2. Principio di indeterminazione (Heisenberg)
Il prodotto dell'incertezza sulla posizione di una particella (Dx) per
l'incertezza sulla sua quantita' di moto (D(mv)) non può essere
inferiore a h/4 (h = costante di Planck).
Dx D(mv) h/4
Se si vuol definire con precisione la quantita' di moto (e quindi
l’energia) di una particella, allora e' impossibile conoscere con
precisione la sua posizione, e viceversa.
15
Principio di indeterminazione: elettrone
Il principio di indeterminazione vale anche per un elettrone in un
atomo: se si vuole determinare la sua energia (che è importante
conoscere con precisione), avremo necessariamente una grande
incertezza sulla sua posizione.
Nel 1927 Schroedinger propose un’equazione la cui risoluzione
fornisce la FUNZIONE D’ONDA di qualunque particella che
possieda proprietà ondulatorie.
La funzione d’onda è una funzione matematica il cui valore varia
con la posizione.
Il concetto di funzione d’onda in quantomeccanica prende il posto
del concetto di traiettoria in fisica classica.
16
8
27/10/2016
Equazione di Schroedinger
Per una particella di massa m che viaggia in una sola dimensione (x) entro
una regione in cui l’energia potenziale sia V(x) l’equazione è la seguente:
- h2/(82m) d2/dx2 + V = E
V(x) = energia potenziale
= funzione d’onda
m = massa della particella
h = costante di Planck
L’equazione si usa sia per calcolare sia la corrispondente energia E.
17
Equazione di Schroedinger
Anche il comportamento di un elettrone in un atomo è descritto dall’equazione di
Schroedinger, la cui risoluzione fornisce una serie di funzioni d’onda .
- h2/(82m) d2/dx2 + V = E
(forma semplificata per una sola dimensione)
Ciascuna funzione d’onda ci dice tutto quello che è noto dello stato fisico
dell’elettrone nell’atomo.
Significato fisico della funzione d’onda (interpretazione di Max Born):
la probabilità di trovare l’elettrone in una data regione dello spazio è
proporzionale a 2 ( 2 = densità di probabilità)
Una funzione d’onda può assumere valori positivi (fase positiva) in alcune
regioni di spazio, valori negativi (fase negativa) in altre.
I punti nei quali la funzione d’onda va a zero sono chiamati nodi.
18
9
27/10/2016
Risoluzione dell’equazione di Schroedinger
L’equazione è usata per calcolare sia la funzione d’onda sia il
corrispondente valore permesso dell’energia.
Schroedinger trovò che i livelli energetici permessi per un elettrone in un
atomo di idrogeno sono:
En = - h R / n2
dove n = numero intero positivo
R = m e e4 /(8h3e02) costante di Rydberg
con me= massa dell’elettrone, e= carica dell’elettrone,
e0= costante dieletttrica del vuoto
quindi
l’energia dell’elettrone è quantizzata (l’elettrone può assumere
solo alcuni valori di energia)
tutti i valori di energia permessa sono negativi
19
Equazione di Schroedinger e orbitali atomici
La risoluzione dell’equazione fornisce i valori esatti delle energie
permesse per l’elettrone nell’atomo di idrogeno
di conseguenza, per il principio di indeterminazione non è possibile
conoscere la posizione dell’elettrone:
si potrà solo parlare di probabilità che un elettrone di energia En
si trovi in una certa regione dello spazio.
Le funzioni d’onda che corrispondono agli stati di energia permessi
per l’elettrone nell’atomo sono chiamate ORBITALI.
Per risolvere l’equazione di Schroedinger nello spazio
tridimensionale è necessario specificare 3 numeri quantici.
20
10
27/10/2016
NUMERI QUANTICI
n numero quantico principale
n = 1,2,3…∞
determina l’energia dell’eletttrone (definisce il GUSCIO o LIVELLO)
l numero quantico angolare
l = 0,1,2…n-1
a ciascun valore di l corrisponde una diversa distribuzione angolare
(= una diversa forma) di orbitale
(definisce il SOTTOLIVELLO)
ml numero quantico magnetico
-l ≤ ml ≤ l
il suo valore regola il comportamento dell’elettrone in
presenza di un campo magnetico esterno;
a ciascun valore di m l corrisponde un orbitale con diversa
orientazione nello spazio (ciascun valore di m l individua un
orbitale del sottolivello)
(definisce l’ORBITALE)
21
Orbitali
atomici
22
11
27/10/2016
Rappresentazione di un orbitale atomico:
SUPERFICIE DEI CONTORNI
entro la quale sussiste il 90% di probabilità di trovare l’elettrone
I tre orbitali s di
minima energia
23
Orbitali
atomici
24
12
27/10/2016
Orbitali di tipo p
25
Orbitali
atomici
26
13
27/10/2016
Orbitali di tipo d
27
Guscio con n=4
28
14
27/10/2016
Orbitali di tipo f
29
15












