ESERCITAZIONE 5
•
•
•
•
•
RICHIAMARE LE RELAZIONI PRINCIPALI SUL MAGNETISMO.
PRESENTARE E CLASSIFICARE I FENOMENI MAGNETICI NEI MATERIALI.
FORNIRE UNA SPIEGAZIONE QUALITATIVA DI TALI FENOMENI.
PRESENTARE I MATERIALI FERRIMAGNETICI ED ANTIFERROMAGNETICI.
DESCRIVERE DA UN PUNTO DI VISTA MACROSCOPICO IL COMPORTAMENTO DEI
MATERIALI FERROMAGNETICI.
• PRESENTARNE LE PROPRIETÀ DI INTERESSE TECNICO.
• PRESENTARE I MATERIALI FERROMAGNETICI DOLCI E DURI.
RICHIAMI DI MAGNETISMO
RICORDIAMO CHE SE SI PONE:
• B = VETTORE INDUZIONE MAGNETICA
• H = VETTORE INTENSITÀ DEL CAMPO MAGNETICO
NEL VUOTO POSSIAMO PORRE:
B = µo H
LA COSTANTE µo SI CHIAMA PERMEABILITÀ MAGNETICA DEL VUOTO E NEL
SISTEMA DI MISURA SI ABBIAMO:
µo = 4 π 10-7 H/m
in pratica approssimato a:
µo = 1,26 10-6 H/m
IN PRESENZA DI UN QUALUNQUE MATERIALE SI PUÒ PORRE:
B = µr µoH
DOVE SI HA:
µr = PERMEABILITÀ RELATIVA DEL MATERIALE.
SI HA:
µr < 1, per materiali diamagnetici.
µr > 1, per materiali paramagnetici.
µr >> 1, per materiali ferromagnetici e ferrimagnetici.
TENENDO CONTO CHE, SALVO CHE PER I MATERIALI FERROMAGNETICI E
FERRIMAGNETICI, µr È SEMPRE MOLTO PROSSIMA AD 1.
SI PUÒ INOLTRE DEFINIRE UN VETTOREM INTENSITÀ DI MAGNETIZZAZIONE:
43
M = (B - Bo)/µ
µ0
DOVE Bo È L’INDUZIONE NEL VUOTO E B L’INDUZIONE CHE SI STABILISCE
QUANDO SI SOSTITUISCE AL VUOTO UN QUALUNQUE MATERIALE.
SI PUÒ ANCHE PORRE:
B = µ0 (H + M)
DOVE M RAPPRESENTA IL MOMENTO MAGNETICO PER UNITÀ DI VOLUME DEL
MATERIALE.
SI DEFINISCE SUSCETTIVITÀ MAGNETICA LA QUANTITÀ:
χm = M/H
DALLE RELAZIONI PRECEDENTI SI OTTIENE:
χm = (µ
µr - 1)
PER MATERIALI DIAMAGNETICI SI HA
M < 0.
NEL VUOTO SI HAM = 0.
PER MATERIALI PARAMAGNETICI SI HA
M > 0.
PER I MATERIALI FERROMAGNETICI E FERRIMAGNETICI SI M
HA
>> 0.
SOLAMENTE I MATERIALI FERROMAGNETICI E
IMPORTANZA PRATICA NELL’INDUSTRIA ELETTRICA
FERRIMAGNETICI
HANNO
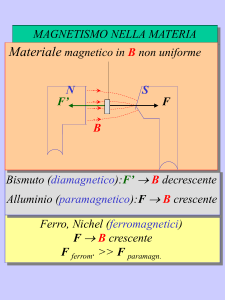
MATERIALI DIAMAGNETICI
Figura 5.1 - Comportamento qualitativo di un materiale diamangnetico
IL CAMPO MAGNETICO VIENE INDEBOLITO ALL’INTERNO DEL MATERIALE. SONO
DIAMAGNETICHE TUTTE LE SOSTANZE. L’EFFETTO È MOLTO DEBOLE
µr circa
(
1,
44
χ circa 10-6), È MASCHERATO DAL PARAMAGNETISMO E DAL
FERROMAGNETISMO.
IN UN MATERIALE DIAMAGNETICO NON ESISTONO DIPOLI MAGNETICI
PERMANENTI. L’APPLICAZIONE DI UN CAMPO MAGNETICO DI INDUZIONE B CREA
DEI DIPOLI MAGNETICI DI DIREZIONE OPPOSTA E QUINDI TALI DA INDEBOLIRE B
(Fig. 5.2 e 5.3).
v0
-e
-e
F
v0
F
r
r
B=0
Figura 5.2 - Materiale diamagnetico in assenza di campo magnetico esterno
FB
v0
-e
-e
FB
F
r
v0
F
r
B≠0
Figura 5.3 - Materiale diamagnetico in presenza di campo magnetico esterno
45
MATERIALI PARAMAGNETICI
Figura 5.4 - Comportamento qualitativo di un materiale paramangnetico
IL CAMPO MAGNETICO VIENE RAFFORZATO ALL’INTERNO DEL MATERIALE.
L’EFFETTO È PIUTTOSTO DEBOLE (µr circa 1, χ = 10-6 - 10-2) ANCHE SE TALE DA
MASCHERARE IL COMPORTAMENTO DIAMAGNETICO.
NEI MATERIALI PARAMAGNETICI SONO PRESENTI DIPOLI MAGNETICI
PERMANENTI DI TIPO ATOMICO:
• PER B = 0 I DIPOLI NON HANNO UNA DIREZIONE PREFERENZIALE;
• PER B DIVERSO DA ZERO I DIPOLI TENDONO AD ORIENTARSI NELLA DIREZIONE
DEL CAMPO RAFFORZANDOLO.
IL FENOMENO È DISTURBATO DALL’AGITAZIONE TERMICA
MATERIALI FERROMAGNETICI
Figura 5.5 - Comportamento qualitativo di un materiale paramangnetico
SI HA UN EFFETTO SIMILE A QUELLO DEI MATERIALI PARAMAGNETICI MA MOLTO
RAFFORZATO (µr dell’ordine di alcune migliaia o decine di migliaia).
I DIPOLI PERMANENTI SONO RAGGRUPPATI IN DOMINI (DETTI DOMINI DI WEISS) I
CUI MOMENTI MAGNETICI NON SONO CONCORDI FRA LORO PER VALORI NULLI O
MOLTO BASSI DI B.
46
SE B CRESCE AUMENTANO LE DIMENSIONI DEI DOMINI CONCORDI CON IL CAMPO
E SI HA ROTAZIONE RIGIDA DI ALTRI DOMINI (Fig. 5.6 e 5.7).
B
ROTAZIONE DEI
MOMENTI MAGNETICI
B
CRESCITA DEI DOMINI
CONCORDI.
CONTRAZIONE DEI
DOMINI DISCORDI
H
Figura 5.6 - Crescita e rotazione dei domini magnetici
H=0
H
H
Figura 5.7 - Spostamento delle pareti dei domini per effetto del campo magnetico esterno
47
MATERIALI FERRIMAGNETICI, ANTIFERROMAGNETICI E
FERROMAGNETICI
MATERIALI ANTIFERROMAGNETICI
SONO MATERIALI PER I QUALI L’ACCOPPIAMENTO DEI DIPOLI MAGNETICI È
RIGOROSAMENTE ANTIPARALLELO. A LIVELLO MACROSCOPICO DIVENTANO
PARAMAGNETICI AL DISOPRA DI UNA CERTA TEMPERATURA (DI NÉEL)
MATERIALI FERRIMAGNETICI
SONO PRESENTI IONI CON DIVERSO MOMENTO MAGNETICO. SI HANNO QUINDI
EFFETTI ESTERNI INTERMEDI FRA I MATERIALI FERROMAGNETICI E QUELLI
ANTIFERROMAGNETICI. ANCHE IN QUESTO CASO AL DISOPRA DI UNA CERTA
TEMPERATURA IL MATERIALE DIVIENE PARAMAGNETICO.
SONO FERRIMAGNETICI ALCUNI MATERIALI CERAMICI CHIAMATI FERRITI. ESSI
HANNO UN VALORE DI PERMEABILITÀ MAGNETICA RELATIVA DELL’ORDINE
DELLE DECINE O DELLE CENTINAIA.
MATERIALI
FERROMAGNETICI
MATERIALI
FERRIMAGNETICI
MATERIALI
ANTIFERROMAGNETICI
Figura 5.8 - Schematizzazione di domini di materiali ferromagnetici, antiferromagnetici e
ferrimagnetici
MATERIALI CON DIVERSO COMPORTAMENTO MAGNETICO.
DIAMAGNETICI: bismuto, rame, argento, stagno, zinco.
PARAMAGNETICI: alluminio, calcio, ossigeno, platino.
FERROMAGNETICI: ferro, cobalto, nichel.
ANTIFERROMAGNETICI: MnO2.
FERRIMAGNETICI: magnetite.
48
DEFINIAMO CURVA DI MAGNETIZZAZIONE DI UN MATERIALE LA CURVA DI B IN
FUNZIONE DI H. DETERMINIAMO TALE CURVA USANDO UN TORO DI MATERIALE
FERROMAGNETICO (Fig. 5.9).
Primario N1
Secondario N2
B
iM
i
R
r
e2
i2
e2
∆t
t
i2
t
Figura 5.9 - Schema per il rilievo della caratteristica di magnetizzazione
SI OTTIENE QUINDI IL VALORE DEL CAMPO:
H = N1 IM/2π
πr
ED IL CORRISPONDENTE VALORE DELL’INDUZIONE MAGNETICA:
e2= N2∆Φ/∆
∆Φ ∆ t = N2BA /∆
∆t
DOVE A È LA SEZIONE DEL TORO.
SE CHIUDIAMO IL SECONDARIO SU UNA RESISTENZA R CIRCOLERÀ UNA
CORRENTE i2 PER UN TEMPO ∆t PARI A:
i2 = e2/R
SI HA QUINDI:
B = e2∆ t/N2A = i2R∆
∆ t/N2A = qR/N2A
49
q = CARICA CHE FLUISCE IN R NEL TEMPO ∆t, SI PUÒ MISURARE CON UN
GALVANOMETRO BALISTICO.
Bs
B (T)
tg α = µmax
α
Hs
H (Asp/m)
Figura 5.10 - Curva di prima magnetizzazione di un materiale ferromagnetico
B (T)
tg α = µi
α
H (Asp/m)
Figura 5.11 - Tratto iniziale della curva di prima magnetizzazione
L’ANDAMENTO DEL TRATTO INIZIALE DELLA CURVA B - H SI PUÒ SPIEGARE CON
UN RITARDO DEI DOMINI AD ORIENTARSI NELLA DIREZIONE DEL CAMPO
MAGNETICO.
50
B (T)
Br
Hc
H (Asp/m)
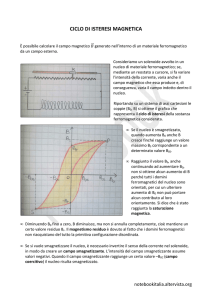
Figura 5.12 - Ciclo di isteresi di un materiale ferromagnetico
IL FENOMENO DELL’ISTERESI IN UN MATERIALE FERROMAGNETICO SI PUÒ
SPIEGARE CON IL FATTO CHE PER B = 0 NON TUTTI I DOMINI RITORNANO
ALL’ORIENTAMENTO INIZIALE.
L’ISTERESI MAGNETICA PRODUCE DELLE PERDITE LA CUI ENTITÀ È
PROPORZIONALE ALL’AREA DEL CICLO.
L’ORIENTAMENTO DEI DOMINI AVVIENE IN MODO DISCONTINUO.
PROPRIETÀ DEI MATERIALI FERROMAGNETICI
LE PROPRIETÀ DI INTERESSE APPLICATIVO SONO:
• L’INDUZIONE DI SATURAZIONE Bs
• IL CAMPO DI SATURAZIONE Hs
• LA PERMEABILITÀ MASSIMAµmax
• LA PERMEABILITÀ INIZIALE µi
DI PARTICOLARE INTERESSE PER I MAGNETI PERMANENTI:
• L’INDUZIONE RESIDUA Br
• LA FORZA COERCITIVA Hc
B (T)
H (Asp/m)
Figura 5.13 - Orientamento dei domini di Weissper effetto del campo
51
MATERIALI FERROMAGNETICI DOLCI E DURI
MATERIALI FERROMAGNETICI DOLCI
SONO CARATTERIZZATI DA UN CICLO DI STERESI STRETTO ED ALTO.
B
SONO CARATTERIZZATI
DA:
ELEVATA µmax
H
ELEVATA Br
BASSO Hc
PICCOLA AREA DEL
CICLO
Figura 5.14 - Ciclo di isteresi di un materiale ferromagnetico dolce
MATERIALI FERROMAGNETICI DURI
SONO CARATTERIZZATI DA UN CICLO DI STERESI BASSO E PANCIUTO.
SONO CARATTERIZZATI
DA:
B
BASSA µmax
H
ELEVATA Hc
GRANDE AREA DEL
CICLO
Figura 5.15 - Ciclo di isteresi di un materiale ferromagnetico duro
ELEMENTI FERROMAGNETICI
GLI ELEMENTI FERROMAGNETICI SONO:
FERRO
COBALTO
NICKEL
FERRO
È L’UNICO ELEMENTO UTILIZZATO ALLO STATO PURO COME MATERIALE
FERROMAGNETICO. PRESENTA PERDITE PER ISTERESI RIDOTTE. SI
SMAGNETIZZA FACILMENTE.
52
È IL COMPONENTE FONDAMENTALE DI MOLTE LEGHE FERROMAGNETICHE.
B
2
Bs = 2,15 Tesla
Br Elevata
1
Hc = 4 As/m
Piccola area del ciclo
µM = 7000
H
µi = 250
(Ferro ARMCO)
Figura 5.16 - Ciclo di isteresi del ferro (ARMCO American Rolling Mill Co)
NICHEL
SI TRATTA DI UN MATERIALE NON INTERESSANTE ALLO STATO PURO.
LE SUE PROPRIETÀ DIPENDONO MOLTO DAI TRATTAMENTI E
LAVORAZIONI. È COSTITUENTE DI MOLTE LEGHE.
DALLE
B
Bs = 0,65 Tesla
0,5
Br Medio - bassa
Hc = 80 As/m
Ciclo tipo mat. duro
H
µM = 2500
µi = 150
Figura 5.17 - Ciclo di isteresi del nichel
COBALTO
È UN MATERIALE CON PERDITE PER ISTERESI ELEVATE. NON È USATO ALLO
STATO PURO, MA RIENTRA IN LEGHE MAGNETICHE, SPECIE PER MAGNETI
PERMANENTI.
ANCHE IL COBALTO È MOLTO SENSIBILE AI TRATTAMENTI TERMICI.
53
B
Bs = 1,8 Tesla
1
Br Media
Hc = 800 As/m
H
Ciclo tipo mat. duro
µM = 250
µi = 70
Figura 5.18 - Ciclo di isteresi del cobalto
B
(Wb/m2 )
2
Fe
Co
1
Ni
H (Aspire/m)
Figura 5.19 - Confronto tra le curve di magnetizzazione di ferro, cobalto e nichel
Fe
B
Ni
Co
H
Figura 5.20 - Confronto tra i cicli d'isteresi di ferro, cobalto e nichel
54