Tema 15-11-2011

DINAMICA DI SISTEMI AEROSPAZIALI
Tema d’esame 15 - 11 - 2011
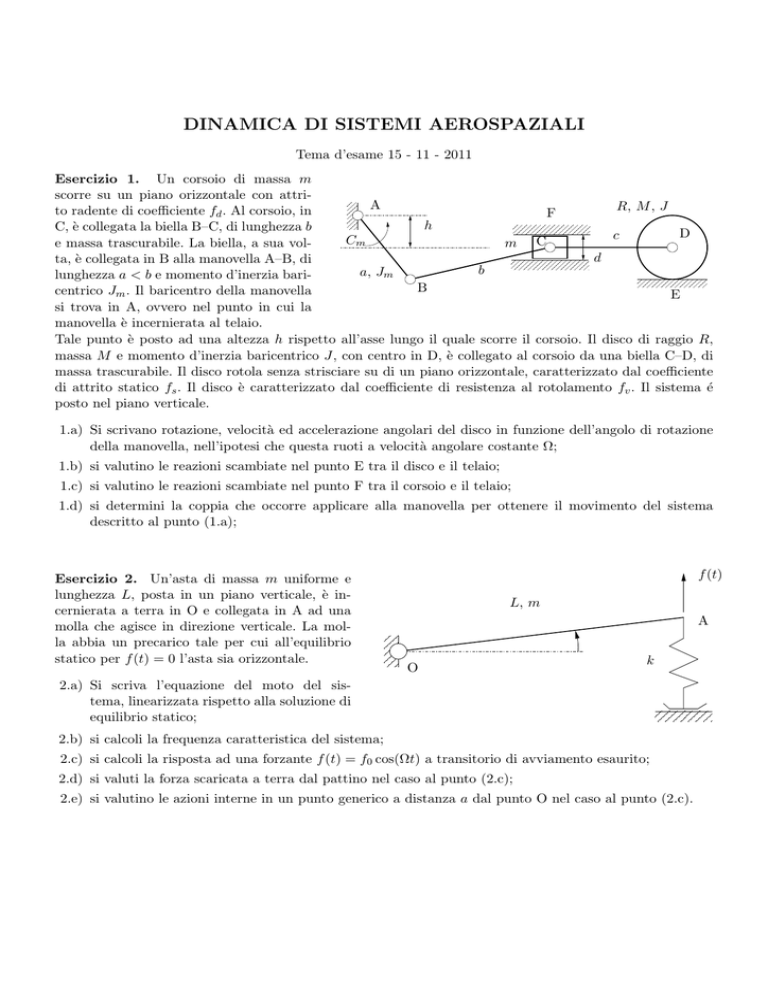
Esercizio 1. Un corsoio di massa m
scorre su un piano orizzontale con attriR, M , J
000 A
111
to radente di coefficiente fd . Al corsoio, in
F
000
111
000
111
h
C, è collegata la biella B–C, di lunghezza b
000000000 c
111111111
000
111
D
000000000
C
C
m
e massa trascurabile. La biella, a sua volm111111111
ta, è collegata in B alla manovella A–B, di
000000000d
111111111
b
a,
J
000000000
111111111
m
lunghezza a < b e momento d’inerzia bari11111111
00000000
B
centrico Jm . Il baricentro della manovella
E
si trova in A, ovvero nel punto in cui la
manovella è incernierata al telaio.
Tale punto è posto ad una altezza h rispetto all’asse lungo il quale scorre il corsoio. Il disco di raggio R,
massa M e momento d’inerzia baricentrico J, con centro in D, è collegato al corsoio da una biella C–D, di
massa trascurabile. Il disco rotola senza strisciare su di un piano orizzontale, caratterizzato dal coefficiente
di attrito statico fs . Il disco è caratterizzato dal coefficiente di resistenza al rotolamento fv . Il sistema é
posto nel piano verticale.
1.a) Si scrivano rotazione, velocità ed accelerazione angolari del disco in funzione dell’angolo di rotazione
della manovella, nell’ipotesi che questa ruoti a velocità angolare costante Ω;
1.b) si valutino le reazioni scambiate nel punto E tra il disco e il telaio;
1.c) si valutino le reazioni scambiate nel punto F tra il corsoio e il telaio;
1.d) si determini la coppia che occorre applicare alla manovella per ottenere il movimento del sistema
descritto al punto (1.a);
Esercizio 2. Un’asta di massa m uniforme e
lunghezza L, posta in un piano verticale, è incernierata a terra in O e collegata in A ad una
molla che agisce in direzione verticale. La molla abbia un precarico tale per cui all’equilibrio
statico per f (t) = 0 l’asta sia orizzontale.
2.a) Si scriva l’equazione del moto del sistema, linearizzata rispetto alla soluzione di
equilibrio statico;
f (t)
11
00
00
11
00 O
11
00
11
L, m
A
k
2.b) si calcoli la frequenza caratteristica del sistema;
1111
0000
2.c) si calcoli la risposta ad una forzante f (t) = f0 cos(Ωt) a transitorio di avviamento esaurito;
2.d) si valuti la forza scaricata a terra dal pattino nel caso al punto (2.c);
2.e) si valutino le azioni interne in un punto generico a distanza a dal punto O nel caso al punto (2.c).
Traccia di soluzione
Esercizio 1.
1.a) Moto del disco. La rotazione ϕ del disco, positiva in senso antiorario, nell’ipotesi di puro rotolamento
è legata alla traslazione y del suo centro D in direzione parallela al piano di rotolamento e positiva verso
destra da
y
ϕ=− .
(1)
R
Dato che il piano di rotolamento è parallelo al piano di strisciamento del corsoio, la traslazione x di quest’ultimo in direzione parallela al piano è uguale alla traslazione del punto D, y. Quindi il moto del disco è legato
al moto del punto C, che a sua volta può essere messo in relazione con quello della manovella A–B attraverso
una equazione di chiusura relativa al triangolo ABC.
Sia α l’angolo di rotazione della manovella, con origine a manovella orizzontale verso destra e verso
positivo antiorario. Sia β l’angolo di rotazione della biella, con le stesse convenzioni. Sia x la componente
orizzontale della distanza del perno C del corsoio dal punto A, positiva verso destra. L’equazione di chiusura
relativa al triangolo ABC è
aejα + bejβ = x − jh;
(2)
scomposta in parte reale ed immaginaria dà
a cos α + b cos β = x
(3a)
a sin α + b sin β = −h,
(3b)
dalle quali si ricava
h a
−1
β = sin
− − sin α
b
b
s
2
h a
x = a cos α + b 1 − − − sin α
b
b
(4a)
(4b)
ovvero β e soprattutto x in funzione di α.
Dalla derivata dell’equazione di chiusura,
j α̇aejα + j β̇bejβ = ẋ
(5)
si ricava
−α̇a sin α − β̇b sin β = ẋ
(6a)
α̇a cos α + β̇b cos β = 0,
(6b)
ovvero
b sin β 1
−b cos β 0
β̇
ẋ
=
−a sin α
a cos α
α̇
(7)
Dalla derivata seconda dell’equazione di chiusura,
j α̈aejα − α̇2 aejα + j β̈bejβ − β̇ 2 bejβ = ẍ
(8)
si ricava
−α̈a sin α − α̇2 a cos α − β̈b sin β − β̇ 2 b cos β = ẍ
2
2
α̈a cos α − α̇ a sin α + β̈b cos β − β̇ b sin β = 0,
(9a)
(9b)
ovvero
b sin β 1
−b cos β 0
β̈
ẍ
=
−a sin α
a cos α
α̈ −
α̇2 a cos α + β̇ 2 b cos β
α̇2 a sin α + β̇ 2 b sin β
.
(10)
A questo punto, il moto del punto C è determinato fino all’accelerazione in funzione di α e delle sue derivate.
In particolare, dal momento che nel caso in esame α̇ = Ω, è possibile operare alcune semplificazioni. È
opportuno notare che, nonostante l’accelerazione angolare della manovella sia nulla, a causa della cinematica
del meccanismo le accelerazioni di alcune parti sono in generale non-nulle.
1.b) Reazioni tra disco e telaio. Nel seguito, per semplicità, si considera la generica condizione di
moto rappresentata in figura alla quale, nell’ipotesi di rotazione antioraria della manovella, corrisponde uno
spostamento di corsoio e disco verso destra, e quindi una rotazione del disco in senso orario.
Dal momento che l’asta C–D ha massa trascurabile e non è sollecitata se non agli estremi, la reazione
vincolare scambiata tra asta e disco può essere diretta soltanto lungo l’asta stessa. Ne consegue che l’equilibrio
alla traslazione del disco in direzione verticale si riduce a
NE = M g.
(11)
Si scriva l’equilibrio alla rotazione del solo disco rispetto al punto C,
−J ϕ̈ + Cv + RTE = 0,
(12)
con TE arbitrariamente scelta come positiva verso destra, da cui si ricava
TE = −
J
ẍ − fv M g.
R2
(13)
1.c) Reazioni tra corsoio e telaio. Si scriva l’equilibrio alla traslazione del solo disco in direzione
orizzontale, considerando la forza HD scambiata con l’asta,
HD + TE − M ẍ = 0;
(14)
si ricava
J
HD = M + 2 ẍ + fv M g.
R
(15)
Si consideri ora l’equilibrio alla rotazione del corsoio rispetto al punto C; la forza dovuta allo strisciamento
si oppone al moto, quindi nel caso in esame e con le ipotesi menzionate in precedenza, la forza è diretta
verso sinistra. Detto W il momento di reazione scambiato con il vincolo e d lo spessore del corsoio, se il
punto F si trova sopra (ovvero se la componente di reazione normale è verso il basso) si ha
d
W + TF = 0
2
(16)
mentre se il punto F si trova sotto si ha
d
W − TF = 0
2
(17)
In ogni caso, questo equivale a considerare la forza TE applicata nel punto C.
Si scriva l’equilibrio alla rotazione del sottosistema costituito dalle aste B–C e C–D e dal corsoio rispetto
al punto B,
b cos βNF − b cos βmg + b sin βTF + b sin βmẍ + b sin βHD = 0
(18)
Siccome TF = fd kNF k, si ha
J
NF − mg + tan β fd kNF k + m + M + 2 ẍ + fv M g = 0
R
(19)
La presenza del modulo non consente di determinare a priori il valore di NF , siccome dipende da come
evolverà il movimento e l’equilibrio del sistema. In ogni caso, si ha
!
!
J
mg − tan β
m + M + 2 ẍ + fv M g
R
NF =
NF > 0
(20a)
1 + tan βfd
!
!
J
mg − tan β
m + M + 2 ẍ + fv M g
R
NF < 0
(20b)
NF =
1 − tan βfd
Questa valutazione può essere svolta a priori dato che il movimento è imposto e quindi β e ẍ sono noti.
1.d) Coppia necessaria. Siccome il sistema ha un solo grado di libertà e non ha vincoli mobili, si può
utilizzare il teorema dell’energia cinetica. L’energia cinetica del sistema è
J
1
1
1
1
1
(21)
Jm α̇2 + m + M + 2 ẋ2 ,
Ec = Jm α̇2 + mẋ2 + mẏ 2 + J ϕ̇2 =
2
2
2
2
2
R
over ẋ = ẋ(α, α̇) è noto dalla cinematica.
La potenza delle forze attive è
Π = Cm α̇ + Πv + Πd ,
(22)
ove Πv rappresenta la potenza dissipata per rotolamento del disco e Πd quella dissipata per strisciamento
del corsoio.
Il calcolo della potenza Πv richiede la componente normale della reazione al contatto tra disco e piano,
NE , la quale consente di calcolare
Πv = − kϕ̇k fv RM g = − kẋk fv M g.
(23)
Il calcolo della potenza Πd richiede la componente normale della reazione al contatto tra corsoio e piano,
NF . Di conseguenza, la potenza dissipata per attrito nelle condizioni ipotizzate è
Πd = − kẋk fd kNF k
Dall’applicazione del teorema dell’energia cinetica si ricava
J
∂x
∂x
∂x
Jm α̈α̇ + m + M + 2 ẍ α̇ = Cm α̇ −
α̇fv M g −
α̇fd kNF k
R
∂α
∂α
∂α
ove i termini ∂x/∂α sono noti dalla cinematica (in assenza di vincoli mobili basta valutare ẋ/α̇).
La coppia necessaria è quindi
∂x
∂x
∂x
J
+
fv M g +
fd kNF k
Cm = Jm α̈ + m + M + 2 ẍ
R
∂α ∂α
∂α
(24)
(25)
(26)
Esercizio 2.
2.a) Equazione del moto linearizzata. Il sistema ha un grado di libertà; conviene utilizzare l’angolo ϑ
di rotazione dell’asta rispetto all’orizzontale in verso antiorario. L’allungamento della molla è u = L sin ϑ,
mentre quello di molla scarica sia u0 . L’equilibrio alla rotazione del sistema rispetto al punto O dà
−JG ϑ̈ − mxG ϑ̈xG − k (L sin ϑ − u0 ) L cos ϑ + f L cos ϑ − mgxG cos ϑ = 0.
Siccome l’asta è uniforme, xG = L/2 e JG = mL2 /12, per cui
L2
L
m ϑ̈ + k (L sin ϑ − u0 ) L cos ϑ = f L − mg
cos ϑ
3
2
(27)
(28)
La soluzione di equilibrio statico indicata corrisponde a ϑ = 0; in tale condizione, per f = 0, si ha
−kLu0 = −mg
L
2
(29)
da cui si ricava la condizione di precarico della molla
u0 =
mg
2k
(30)
La linearizzazione rispetto a ϑ = 0 porta a scrivere
m
L2
ϑ̈ + kL2 ϑ = f L
3
(31)
2.b) Frequenza caratteristica. È
s
v
u
2
kL
3k
u
ω0 = u
=
t L2
m
m
3
(32)
2.c) Risposta a forzante armonica. La risposta sia del tipo ϑ = Θ cos(Ωt), con Ω 6= ω0 . Nell’ipotesi che
lo smorzamento, abbastanza piccolo da essere trascurato nella scrittura dell’equazione del moto, sia tuttavia
presente e sufficiente a far annullare, in un tempo sufficientemente lungo, il movimento libero del sistema,
si ha
2
2 L
2
−Ω m
+ kL Θ = f0 L
(33)
3
da cui si ricava
L
Θ=
kL2
−
Ω2 m
L2
3
f0
(34)
2.d) Reazione al pattino. La reazione al pattino è data dalla forza che attraversa la molla, ovvero
RN = k (L sin ϑ − u0 ) = −
mg
+ kL sin (Θ cos(Ωt))
2
(35)
ovvero una parte costante dovuta al peso dell’asta (metà, per l’esattezza) e una parte variabile dovuta alla
risposta alla forzante.
2.e) Azioni interne. Sono dovute al peso e alle forze d’inerzia distribuite nell’asta.