Università degli studi di Roma
“Tor Vergata”
Facoltà di Scienze MM. FF. NN.
TFA
STORIA E DIDATTICA DELLE SCIENZE ESATTE
Prof. LUCIO RUSSO
TRIANGOLI: PROPRIETA’ E CRITERI
DI
CONGRUENZA NEGLI ELEMENTI DI
EUCLIDE
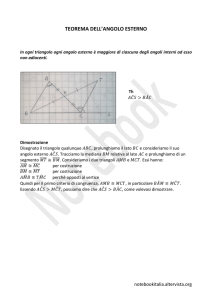
Tirocinante: ANDREA TRUSIANO Roma, 24 Giugno 2013 Anno Accademico 2012-­‐2013 1) IL PRIMO LIBRO DEGLI ELEMENTI, TERMINI, POSTULATI E NOZIONI COMUNI Il primo libro degli elementi di Euclide inizia bruscamente con un elenco di ventitré definizioni (termini) tra cui quelle di punto, linea, superficie, angolo piano retto, ottuso e acuto, figura, figura trilatera (triangolo equilatero, isoscele e scaleno), cerchio, figure quadrilatere (quadrato, rettangolo, rombo, romboide, trapezio) e si conclude con la definizione di rette parallele. La debolezza di questa parte sta nel fatto che alcune definizioni in realtà non definiscono nulla. Infatti non c’è nessun elenco preliminare di elementi indefiniti, in termine dei quali si debbano definire gli altri elementi. Ad esempio la definizione euclidea di angolo piano come “l’inclinazione l’una rispetto all’altra di due rette giacenti in un piano le quali si incontrano ma non sono in linea retta”, è viziata dal fatto che il termine “inclinazione” non è stato definito precedentemente e non è più noto del termine “angolo”. Dopo le definizioni, Euclide elenca cinque postulati. Essi sono proposizioni dal carattere molto semplice riguardanti gli enti introdotti nelle definizioni, si tratta di proposizioni che non vengono dimostrate ma che sono arbitrariamente ipotizzate come vere (citando Aristotele, i postulati sono proposizioni che devono essere convincenti di per se stesse, sono verità comuni a tutte le scienze). 2 Postulati: 1) Che si possa tracciare una retta da un punto qualsiasi a un punto qualsiasi 2) Che si possa prolungare indefinitamente una linea retta 3) Che si possa descrivere un cerchio con un centro qualsiasi e un raggio qualsiasi 4) Che tutti gli angoli retti siano uguali 5) Che se una retta venendo a cadere su due rette forma dalla stessa parte angoli interni inferiori a due angoli retti, le due rette, prolungate illimitatamente si incontrano da quella parte dove gli angoli sono inferiori a due angoli retti L’interpretazione dei postulati è fondamentale per la comprensione di tutta l’opera euclidea. Sembrerebbe che i postulati I, II e III si riferiscano direttamente alla possibilità di eseguire determinate costruzioni: precisamente i postulati I e II riguardano la costruzione di rette, mentre il postulato III riguarda la costruzione di cerchi. Sembrerebbe quindi che i suddetti postulati corrispondano all’uso della riga e del compasso. Osserviamo però che Euclide non nomina mai gli strumenti in questione, egli parla ad un livello più astratto, sostituendo alla riga e al compasso, dei modelli teorici degli strumenti reali, capaci di compiere le operazioni descritte nei primi tre postulati. La costruzione del segmento di retta che congiunge due punti (postulato I) e il prolungamento a piacere di un segmento (postulato II) corrispondono effettivamente 3 all’uso classico della riga, ma non si può dire lo stesso per l’uso del compasso nella costruzione del cerchio alla quale si riferisce il postulato III. Il nostro modo comune di usare il compasso ci permette di fare quanto segue: dato un segmento AB in una posizione qualsiasi sul piano, e dato un punto C del piano, possiamo costruire il cerchio di centro C e raggio uguale ad AB eseguendo il trasporto del segmento. Cioè possiamo aprire il compasso su AB, e poi trasportarlo, così aperto, fino a collocarlo con una punta in C. Euclide non richiede tanto al suo terzo postulato. Dobbiamo pensare al compasso di Euclide come ad uno strumento astratto che si richiude non appena le sue due punte vengono sollevate dal foglio1. L’ultima cosa che viene introdotta da Euclide prima di enunciare e dimostrare i suoi teoremi, sono le “Nozioni comuni”. Anche in questo caso si tratta di proposizioni dal carattere molto generale che vengono enunciate e considerate vere senza che siano dimostrate. A differenza dei postulati però, l’argomento di queste proposizioni non è strettamente geometrico, infatti in esse si parla genericamente di “cose” e di operazioni non meglio specificate come “raddoppiare”, “addizionare”, ecc. 1 Ciò non si rileva direttamente dall’enunciato del terzo postulato ma dalla seconda e dalla terza proposizione del libro I. 4 Nozioni comuni: 1) Cose uguali2 a una medesima cosa sono uguali anche tra loro 2) Se cose uguali vengono aggiunte a cose uguali, i totali sono uguali 3) Se da cose uguali vengono sottratte cose uguali, i resti sono uguali 4) Se cose disuguali sono addizionate a cose uguali, i totali sono disuguali 5) I doppi di una stessa cosa sono uguali tra loro3 6) Le metà di una stessa cosa sono uguali tra loro4 7) Cose che si sovrappongono tra loro sono uguali tra loro5 8) L’intero è maggiore della parte Osserviamo che la prima nozione comune non è nient’altro che la proprietà transitiva dell’ugualianza. La seconda e la terza invece ci offrono i criteri di uguaglianza per somma e per differenza. Esse, se applicate ai poligoni, si riferiscono all’ugualianza di grandezze (equivalenza)6. La penultima (VII) nozione se presa alla lettera, enuncerebbe la proprietà riflessiva dell’ugualianza. Ma l’uso tipico che ne fa Euclide non è per le figure che già sicuramente coincidono, bensì per quelle che si fanno coincidere mediante un 2 La parola uguale (ìsos) viene usata da Euclide nel senso dell’ugualianza estensiva, ciò corrisponderebbe per i poligoni, ad esempio, al nostro termine equivalente. 3 Si può ricavare dalla seconda nozione comune. 4 Si può ricavare dalla terza nozione comune. 5 Per “sovrapporre” Euclide intende che due figure possono essere portate a coincidere esattamente mediante un movimento rigido, cioè senza che vengano deformate nel movimento. 6 Infatti, somme o differenze di poligoni uguali in senso stretto (congruenti) non sono congruenti, ma equivalenti. 5 movimento. Egli infatti, per dimostrare l’ugualianza tra due figure A e B, muove la figura A fino a farla coincidere con B, e poi ricorre alla nozione comune VII per affermare che A e B sono uguali, dato che A (nella sua nuova posizione) coincide con B. Il fatto che la figura , nella posizione finale, sia uguale alla figura nella posizione iniziale non viene messo in discussione da Euclide. Egli considera il movimento nel senso intuitivo, maccanico. È bene notare che, nella sua opera, Euclide fa un uso molto ridotto del movimento rigido7, probabilmente perché ne riconosce la natura extra-­‐
geometrica. L’ultima nozione comune, se applicata (ad esempio) ai segmenti, può essere considerata un abbozzo delle proprietà di ordine dei punti della retta, per il fatto che permette di ottenere un ordine crescente (perchè il maggiore del maggiore risulta pure maggiore). Notiamo che quest’ultima nozione comune non è valida per insiemi infiniti. 2) IL PRIMO CRITERIO DI CONGRUENZA DEI TRIANGOLI Subito dopo i postulati e le nozioni comuni, negli Elementi di Euclide, comincia il ciclo delle 48 proposizioni del libro I. Ogni proposizione è seguita da una dimostrazione giustificata da definizioni, postulati, nozioni comuni o da una proposizione 7 Solamente in I, 4 in I, 8 e in III, 24. 6 dimostrata precedentemente. Spesso le dimostrazioni sono corredate da disegni illustrativi. È da notare che alcune proposizioni sono, in realtà, delle costruzioni. La dimostrazione delle costruzioni è strutturata nel seguente modo: come prima cosa Euclide descrive come eseguire la costruzione, poi si preoccupa di mostrare che la costruzione proposta soddisfa le richieste della proposizione. Le prime quattro proposizioni sono le seguenti: 1) Costruire, su di una retta limitata data, un triangolo equilatero. 2) Porre su un punto dato una retta uguale alla retta data. 3) Date due rette disuguali, sottrarre dalla maggiore una retta uguale alla minore. 4) Primo criterio di congruenza dei triangoli: Se due triangoli hanno due lati rispettivamente uguali a due lati e l’angolo tra essi compreso uguale all’angolo, allora avranno anche la base uguale alla base e il triangolo sarà uguale al triangolo, e i restanti angoli (sotto cui si tendono i lati uguali) saranno rispettivamente uguali ai restanti angoli. La prima delle proposizioni proposte da Euclide offre un procedimento meccanico per costruire un triangolo equilatero di lato dato. Dato un segmento AB, si disegna il triangolo equilatero ABC costruendo i due cerchi di centri A e B e di raggio AB e congiungendo con A e con B uno dei punti (C) di intersezione delle due circonferenze descritte prima. In questo modo i segmenti AC e BC risultano essere raggi delle due 7 circonferenze e quindi il triangolo ABC è equilatero. Questa dimostrazione (che a prima vista sembrerebbe impeccabile) fa in realtà uso di un postulato non espresso precedentemente. Euclide infatti assume, senza dimostrarlo, che i due cerchi si intersechino in un punto. Per restaurare questa mancanza bisognerebbe aggiungere ai postulati un altro postulato equivalente al principio di continuità. La seconda e la terza proposizione costituiscono una precisazione del III postulato e rivelano una grande finezza logica. In pratica esse tolgono dalla portata del III postulato ciò che può essere ottenuto con altri metodi. In particolare la proposizione 2 mostra come costruire un segmento uguale ad un segmento dato e avente un estremo in un punto assegnato. La costruzione proposta da Euclide è la seguente: Facendo riferimento alla Figura 1, inizialmente sono dati il punto A e il segmento BC. Figura 1 8 Come prima cosa si costruisce il triangolo equilatero ABD di lato AB (secondo quanto illustrato nella prima proposizione). Poi si traccia la circonferenza di centro B e raggio BC che incontra la semiretta DB nel punto E. Successivamente si traccia la circonferenza di centro D e raggio DE che incontra la semiretta DA nel punto F. AF è il segmento cercato. Infatti: AF=DF-­DA, DF=DE e DA=DB, quindi AF=BE=BC. Anche la terza proposizione è una costruzione geometrica che stabilisce come portare un segmento dato su di una semiretta assegnata. Euclide fa uso della proposizione 2 per mostrare che, dati due segmenti rettilinei disuguali, è possibile tagliare via dal maggiore un segmento uguale al minore. La costruzione proposta da Euclide è la seguente: Facendo riferimento alla Figura 2, sia AB il segmento che deve essere sottratto da CD. Figura 2 Per prima cosa si applica la costruzione descritta nella proposizione 2 per copiare il segmento AB a partire da C in CE. Successivamente si traccia la circonferenza avente centro in C 9 e raggio pari a CE. Tale circonferenza interseca il segmento CD nel punto F. FD è il segmento cercato. Analizziamo ora la quarta proposizione, meglio nota come primo criterio di congruenza dei triangoli. Ricordiamo che nell’accezione moderna del termine, per “triangoli uguali”, si intende “triangoli identici”, cioè perfettamente sovrapponibili, ovvero aventi tutti i lati e tutti gli angoli uguali. Per Euclide, invece, “triangoli uguali” significa solo “triangoli equivalenti”, cioè aventi la stessa estensione superficiale. Per questo motivo nell’enunciato della quarta proposizione viene specificato esplicitamente che i due triangoli hanno tutti gli elementi corrispondenti (lati e angoli) uguali. La dimostrazione proposta da Euclide può essere riassunta come segue: Facendo riferimento alla Figura 3, siano ABC e DEF due triangoli tali che AB=DE, BC=EF e l’ angolo ABC=DEF. A questo punto Euclide afferma di poter trasportare il segmento DE su AB con il vertice E coincidente con B (analizzeremo in seguito la liceità di tale trasporto). Figura 3 10 Dato che i due segmenti (DE e AB) sono uguali per ipotesi, anche A coincide con D. A questo punto si osserva che le semirette BC ed EF coincidono essendo gli angoli ABC e DEF uguali per ipotesi e quindi il vertice C verrà a coincidere con il vertice F. Essendo allora AC coincidente con DF, sarà anche AC=DF, BAC=EDF e ACB=DFE che era quanto si voleva dimostrare. Osserviamo che in questa dimostrazione viene applicato il movimento rigido di figure senza che tale movimento sia stato precedentemente definito: si tratta del movimento nel senso meccanico della parola. Euclide aveva sicuramente compreso la portata della questione. Infatti è stato riconosciuto che la proposizione 4 viene utilizzata da Euclide come se fosse un vero e proprio postulato8 che giustifica il movimento rigido delle figure. Euclide aveva quindi capito che la proposizione 4 costituisce un vero e proprio postulato. Il perché egli non abbia aggiunto un postulato che giustifichi il trasporto rigido rimane un mistero. Se si analizzano gli altri due criteri di uguaglianza (questo verrà fatto nel seguito di questa trattazione), essi si fondano a loro volta sul primo criterio ed Euclide cerca di limitarne il contenuto al minimo possibile, risalendo, quando non può farne a meno, direttamente alla proposizione 4. Questo è un procedimento caratteristico che Euclide utilizza per i postulati. Sarebbe stato sufficiente aggiungere un tale postulato per rendere la dimostrazione della proposizione 4 8 Si veda l’uso che viene fatto della proposizione 4 nella dimostrazione della proposizione 34 del libro I. 11 più vicina ad una dimostrazione nel senso moderno del termine. Nelle sue prime quattro proposizioni Euclide alterna un impeccabile rigore ad una sorta di grossolanità9. Tale questione può essere risolta ammettendo che le prime quattro proposizioni costituiscano una sorta di prolungamento dei postulati. 3) TRIANGOLI ISOSCELI La proposizione 5 del primo libro degli Elementi è nota come il teorema del triangolo isoscele. Questa proposizione viene anche detta pons asinorum (ponte degli asini), da un lato perché il disegno utilizzato da Euclide nella dimostrazione assomiglia ad un ponte (si veda la Figura 4), dall’altro perché è considerata la prima proposizione non banale presente negli Elementi. È come se fosse un ponte verso le proposizioni di più difficile comprensione presenti nel seguito dell’opera. Se uno studente riesce ad “attraversare” tale ponte, allora sarà pronto ad affrontare le proposizioni successive. Proposizione 5: Gli angoli sulla base dei triangoli isosceli sono uguali tra loro, e, prolungate avanti le rette uguali, gli angoli sotto la base saranno uguali tra loro. 9 Infatti nella proposizione 1 tralascia la dimostrazione che le due circonferenze usate per la costruzione del triangolo equilatero si intersechino effettivamente in un punto ed utilizza questa costruzione nella dimostrazione delle proposizioni 2 e 3. 12 Per la dimostrazione facciamo riferimento alla Figura 4. Figura 4 Sui prolungamenti dei lati AB e AC, consideriamo due segmenti BD e CE tra loro uguali. Anche i segmenti AD e AE saranno tra loro uguali in quanto somma di segmenti uguali10. Consideriamo ora i triangoli ADC e AEB, essi hanno: AD=AE, AC=AB (per ipotesi) e l’angolo BAC in comune. Quindi sono uguali per il primo criterio di uguaglianza dei triangoli. In particolare DC=EB, l’angolo ADC congruente all’angolo AEB e l’angolo ABE congruente all’angolo ACD. Consideriamo ora i triangoli DCB e EBC, essi hanno: DC=EB, BD=CE e gli angoli BDC e CEB congruenti come dimostrato precedentemente. Quindi anche essi sono uguali per il primo criterio di congruenza. In particolare l’angolo CBD è congruente all’angolo BCE e l’angolo BCD è congruente all’angolo CBE. Dato che avevamo già mostrato che ACD=ABE, gli angoli alla base del triangolo isoscele risultano congruenti per differenza di angoli congruenti11. 10 Seconda nozione comune: somme di cose uguali sono uguali. 11 Terza nozione comune: differenze di cose uguali sono uguali. 13 La proposizione 6 è l’inverso della proposizione 5, essa è infatti nota come teorema inverso del triangolo isoscele. L’enunciato del teorema è il seguente: Proposizione 6: Qualora due angoli di un triangolo siano uguali tra loro, anche i lati che si tendono sotto gli angoli uguali saranno uguali tra loro. Euclide dimostra questa proposizione per assurdo. Con riferimento alla figura 5, supponiamo che i lati AB e AC non siano uguali. Sia quindi AB>AC. Figura 5 In questo caso esisterà un punto D sul lato AB tale che DB=AC12. Consideriamo i triangoli ABC e DBC, essi hanno: DB=AC, la base BC in comune e gli angoli ACB e DCB congruenti per ipotesi. I due triangoli considerati risultano uguali per il primo criterio. Questo è però in contraddizione con l’ottava nozione comune, che afferma che il tutto è maggiore della 12 Costruzione dimostrata nella proposizione 3. 14 parte, poiché il triangolo DBC è una parte del triangolo ABC. In questo modo la proposizione è dimostrata. 4) IL TERZO CRITERIO DI CONGRUENZA DEI TRIANGOLI Quello che oggi è noto come il terzo criterio di congruenza dei triangoli viene presentato negli Elementi di Euclide per secondo. Esso si trova nella proposizione 8 del primo libro, mentre quello che attualmente viene indicato come secondo criterio di congruenza è introdotto successivamente13. Per analizzare il criterio e la dimostrazione proposta da Euclide, abbiamo bisogno di introdurre la settima proposizione del libro I: Proposizione 7: Sulla stessa retta altre due rette rispettivamente uguali alle stesse due rette <e> che hanno gli stessi limiti delle rette in origine non saranno costruite verso punti differenti dalla stessa parte14. 13 Proposizione 26 del primo libro. 14 In termini moderni esprimeremo questa proposizione in questo modo: “Dato un segmento, se da ciascuno dei suoi estremi si conducono due segmenti che si incontrano in un punto. Non è possibile costruire con gli 15 Nella dimostrazione di questa proposizione, Euclide procede per assurdo. Facendo riferimento alla Figura 6, supponiamo che ci siano AD e BD, uguali rispettivamente ad AC e BC, che si incontrano in un punto D diverso da C. Figura 6 L’angolo CDA è maggiore dell’angolo BDC in quanto il secondo è una parte del primo. D’altra parte il triangolo BDC è isoscele per ipotesi, quindi BDC=BCD15. Inoltre l’angolo BCD è maggiore dell’angolo DCA in quanto quest’ultimo è in esso contenuto. Abbiamo quindi la seguente serie di disuguaglianze: CDA > BDC = BCD > DCA, da cui ricaviamo che CDA > DCA. Ora, dato che anche il triangolo ACD è isoscele, deve essere CDA = DCA. Abbiamo raggiunto l’assurdo ed il teorema risulta quindi dimostrato. stessi estremi e dalla stessa parte altri due segmenti rispettivamente uguali a quelli costruiti prima ed aventi un diverso punto di intersezione”. 15 Proposizione 5 del libro I. 16 Una volta dimostrata questa proposizione, il terzo criterio di congruenza dei triangoli risulta essere una sua diretta conseguenza. Terzo criterio di congruenza dei triangoli: Qualora due triangoli abbiano i due lati rispettivamente uguali ai due lati, e abbiano anche la base uguale alla base, avranno anche l’angolo compreso dalle rette uguali uguale all’angolo. Per la dimostrazione facciamo sempre riferimento alla Figura 6. Dato che i due triangoli hanno per ipotesi la stessa base, due dei vertici (A e B) possono essere portati a coincidere mediante un movimento rigido che sovrappone la base di uno dei due triangoli con la base dell’altro (notiamo che Euclide utilizza anche in questa dimostrazione la costruzione fatta per dimostrare la proposizione 4). Ragionando per assurdo, se il terzo vertice C del primo triangolo non coincidesse con il terzo vertice D del secondo, avremmo due segmenti uguali con gli stessi estremi che si incontrano in due punti diversi. Questo è in contraddizione con la proposizione 7 dimostrata precedentemente. Quindi anche i terzi vertici coincidono. In conseguenza di ciò ciascuno degli angoli del primo triangolo ha i lati coincidenti con quelli del corrispondente angolo nel secondo triangolo, quindi anche gli angoli risultano uguali. 17 5) IL TEOREMA DELL’ANGOLO ESTERNO E LA CLASSIFICAZIONE DEI TRIANGOLI Quello che oggi chiamiamo teorema dell’angolo esterno, corrisponde alla proposizione 16 degli Elementi. Tale proposizione esprime una disuguaglianza, afferma che in un triangolo ogni angolo esterno è maggiore di ciascun angolo interno ad esso non adiacente. Nella sua dimostrazione Euclide utilizza il primo criterio di uguaglianza. Vediamolo nel dettaglio. Teorema dell’angolo esterno: Prolungando avanti uno solo dei lati di ogni triangolo, l’angolo all’esterno è maggiore di uno e dell’altro degli angoli all’interno e opposti. Per la dimostrazione facciamo riferimento alla figura 7. Figura 7 18 Prolunghiamo il lato BC del triangolo dalla parte di C. Si vuole mostrare che l’angolo ACD è maggiore dell’angolo BAC e dell’angolo ABC. Indichiamo con E il punto medio del lato AC, tracciamo la semiretta BE sulla quale consideriamo il segmento EF=BE16. Consideriamo ora i triangoli ABE e CEF, essi risultano uguali per il primo criterio di uguaglianza (BE=EF per costruzione, AE=EC sempre per costruzione e gli angoli AEB e CEF sono congruenti perché opposti al vertice). In particolare l’angolo BAE è congruente all’angolo ECF . Essendo l’angolo ECF compreso nell’angolo ACD, in base all’ottava nozione comune (il tutto è maggiore della parte), possiamo affermare che: ACD > ECF = BAC. Questo dimostra la prima parte della tesi. Rimane da dimostrare che ACD > ABC. Per fare ciò basta ripetere i passaggi utilizzati precedentemente considerando come angolo esterno BCG ottenuto prolungando il lato AC dalla parte di C. Considerando poi il punto medio di BC e ripercorrendo la costruzione precedente arriveremo a dimostrare che l’angolo BCG è maggiore dell’angolo ABC, e dato che BCG è congruente ad ACD (perché opposti al vertice), possiamo concludere che ACD > ABC e questo conclude la dimostrazione. Nelle successive proposizioni proposte da Euclide nel primo libro degli Elementi, alcune possono essere considerate dei corollari del teorema dell’angolo esterno e saranno utili per classificare i triangoli in base agli angoli. In particolare: 16 In questa costruzione si è fatto ricorso al secondo postulato, il quale afferma che si può prolungare indefinitamente un segmento (quindi indipendentemente da quanto sia lungo BE si può sempre riportare un segmento EF tale che BE=EF sul prolungamento di BE). 19 • Due angoli sostituiti in ogni modo di ogni triangolo sono minori di due retti17 [in ogni triangolo la somma di due angoli è sempre minore di un angolo piatto]. • In un triangolo può esserci solo un angolo maggiore o uguale all’angolo retto. • Gli angoli alla base di un triangolo isoscele sono acuti. Classificazione dei triangoli: Triangoli acutangoli: aventi tutti e tre gli angoli acuti Triangoli ottusangoli: aventi un angolo ottuso e due acuti Triangoli rettangoli: aventi un angolo retto e due acuti 6) IL SECONDO CRITERIO DI CONGRUENZA DEI TRIANGOLI La proposizione 26 del primo libro degli Elementi è oggi nota come secondo criterio di congruenza dei triangoli generalizzato. Nei moderni libri di scuola per secondo criterio di congruenza, si intende il criterio in base al quale due triangoli aventi uguali due angoli e il lato tra essi compreso sono congruenti. Euclide nella sua ventiseiesima proposizione fornisce un enunciato meno restrittivo nel quale afferma che due triangoli sono congruenti se hanno due angoli ed un lato congruenti (il lato congruente non deve necessariamente essere quello compreso tra gli angoli congruenti). 17 Proposizione 17. 20 Secondo criterio di congruenza dei triangoli: Qualora due triangoli abbiano due angoli rispettivamente uguali a due angoli e un solo lato, o quello agli angoli uguali oppure quello che si tende sotto uno solo degli angoli uguali, uguale a un solo lato, avranno anche i restanti lati [rispettivamente] uguali ai restanti lati, e il restante angolo al restante angolo. Euclide suddivide la dimostrazione in due parti, considerando prima il caso in cui il lato congruente sia compreso tra gli angoli congruenti e successivamente il caso generale di due angoli ed un lato qualsiasi congruenti. Dimostriamo il primo caso facendo riferimento alla figura 8. Figura 8 Euclide dimostra la proposizione per assurdo. Siano ABC e DEF due triangoli aventi BC=EF, l’angolo ABC uguale all’angolo DEF e l’angolo ACB uguale all’angolo DFE. Se AB fosse diverso da DE (ad esempio AB < DE), esisterebbe un punto G appartenente al prolungamento del lato BA, tale che BG=DE. I due triangoli BCG e EFD, sarebbero quindi 21 congruenti per il primo criterio di congruenza, in particolare l’angolo BCG sarebbe uguale all’angolo EFD. Per ipotesi l’angolo ACB è uguale all’angolo DFE e quindi dovrebbe essere GCB = ACB, ma questo è assurdo poiché l’angolo ACB è contenuto nell’angolo GCB. Analogamente si dimostra che non può essere neanche AB > DE, quindi dovrà necessariamente essere AB=DE. Dimostrando che AB=DE, si ricade nelle ipotesi del primo criterio. Quindi i due triangoli sono uguali. Vediamo ora la dimostrazione nel caso in cui il lato congruente non sia quello compreso tra i due angoli congruenti. Facendo riferimento alla figura 9, siano gli angoli ABC e ACB del primo triangolo rispettivamente uguali agli angoli DEF e DFE del secondo triangolo e sia AB=DE. Figura 9 Se, per assurdo, BC ed EF non fossero uguali (supponiamo BC > EF), esisterebbe un punto H sul lato BC tale che BH=EF. I due triangoli ABH e DEF sarebbero quindi uguali per il primo criterio di congruenza e in particolare l’angolo AHB risulterebbe uguale all’angolo DFE. Ma, per ipotesi, gli angoli ACB e DFE sono congruenti e quindi ACB=AHB. Questo è in contraddizione con il teorema dell’angolo esterno, infatti 22 considerando il triangolo ACH, gli angoli AHB e ACH sono rispettivamente l’angolo esterno e uno degli angoli interni ad esso non adiacenti. Analogamente si dimostra che non può essere neanche BC < EF e quindi necessariamente dovrà essere BC=EF. Una volta provato ciò si ricade nelle ipotesi del primo criterio di congruenza e possiamo quindi concludere che i due triangoli sono uguali. 23