Facoltà di Ingegneria

Facoltà di Ingegneria
Prova scritta di Fisica I – NO & VO - 22-09-03
Esercizio n.1
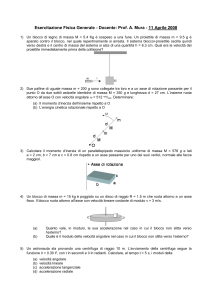
Una pallina, assimilabile ad un punto materiale di massa m = 1 kg, viene lanciata orizzontalmente sopra un tavolo da
N
una molla di costante elastica k = 500
, fissata ad un estremo ed inizialmente compressa di ∆x (vedi figura). La
m
pallina, che non è legata alla molla, prima scivola sul
∆x
tavolo, poi cade ed arriva a terra ad una distanza
d=2.20m dal tavolo. Il tempo di caduta è di 0.5 s.
Trascurando tutti gli attriti, si calcoli:
• La velocità con cui la pallina lascia il tavolo
• L’altezza del tavolo
• La compressione della molla
• L’energia potenziale elastica della molla
compressa
d
• Il modulo della velocità con cui la pallina
arriva a terra
Si risponda quindi alle seguenti domande:
1. La pallina lascia il tavolo con una velocità orizzontale pari a:
m
A. 10.4
s
m
B. 30.1
s
m
(*)
C. 4.4
s
m
D. 0.85
s
2. L’altezza del tavolo risulta
A. 1.22 m (*)
B. 3.55 m
C. 6.76 m
D. 9.81 m
3. La compressione ∆x della molla risulta
A. 20.13 cm
B. 19.68 cm (*)
C. 8.07 cm
D. 3.96 cm
4. L’energia potenziale elastica della molla compressa vale
A. 45.75 J
B. 23.14 J
C. 9.68 J (*)
D. 0.016 J
5. Il modulo della velocità con cui la pallina arriva a terra è
m
A. 0.38
s
m
B. 14.37
s
m
C. 10.61
s
m
(*)
D. 6.59
s
Esercizio n.2
Una pallottola di massa m = 10 g è sparata contro un pendolo balistico di
massa M = 2 kg (vedi figura). Dopo l’urto, la pallottola rimane nel blocco ed
il sistema pallottola-blocco sale fino ad una altezza di h = 20 cm. Trovare
M
h
• il modulo v o della velocità iniziale della pallottola
m
vo
•
il modulo della velocità v con cui il sistema pallottola-blocco ripassa per la posizione verticale
(Suggerimento: nell’urto, la cui durata è trascurabile, non essendoci forze esterne nella direzione orizzontale, la quantità
di moto del sistema pallottola-blocco lungo la direzione orizzontale si conserva)
Rispondere quindi alle seguenti domande:
6. Il modulo della velocità del sistema pallottola-blocco subito dopo l’urto (e cioè prima di iniziare il moto verso
l’alto) ha espressione
m
A.
v o (*)
m+M
m
B.
vo
M
C. v o
M−m
vo
D.
M
7. Quando il sistema pallottola-blocco si muove verso l’alto si conserva:
A. La quantità di moto
B. Il momento angolare
C. L’energia cinetica
D. L’energia meccanica (*)
8. Nel punto di altezza massima, il modulo della velocità del sistema pallottola-blocco ha espressione
m
vo
A.
M
m+M
B.
vo
m
M−m
vo
C.
M
D. 0 (*)
9. Il modulo della velocità iniziale v o del proiettile vale:
m
A. 28.06
s
m
B. 116.21
s
m
C. 397.96
(*)
s
m
D. 713.81
s
10. Il modulo della velocità v con cui il sistema pallottola-blocco ripassa per la posizione verticale
m
A. 0.06
s
m
B. 1.98
(*)
s
m
C. 8.03
s
m
D. 12.71
s
Esercizio n.3
Una ruota di raggio R e momento di inerzia I è libera di ruotare (non c’è attrito) intorno ad un asse
orizzontale passante per il suo centro O. Intorno alla ruota è avvolto un filo inestensibile e di massa
R
trascurabile al cui estremo è appeso un blocchetto di massa m.
O
Il blocco viene lasciato libero da fermo ed il filo si svolge mettendo la ruota in rotazione. Si
determini:
• la tensione del filo
• l’accelerazione del blocco m
m
• il modulo della velocità v con cui si muove il blocco dopo essere sceso di una distanza h
• l’energia cinetica della ruota nell’istante in cui il blocco è sceso di una distanza h
h
Rispondere poi alle seguenti domande:
11. Il modulo della tensione T del filo ha espressione
mg
A. T =
I + 2mR 2
Im g
(*)
B. T =
I + mR 2
Ig
C. T =
mR 2
I + mR 2
D. T =
g
m
12. Il modulo dell’accelerazione a del blocco ha espressione
mg
A. a =
m+I
mg
B. a =
mR 2 + 2I
2mg
C. a =
mR 2 + I
R 2 mg
D. a =
(*)
mR 2 + I
13. Il modulo della velocità v con cui si muove il blocco alla distanza h.
A.
B.
2R 2 mg
h (*)
mR 2 + I
2Rmg
v=
h
mR 2 + I
v=
C.
v=
D.
v=
2R 2 h
I
2g
(
)
h
mg R 2 + I
14. L’energia cinetica della ruota quando il blocco è alla distanza h (ed ha quindi velocità v)
1
A.
mv 2
2
1 2
Iv
B.
2
1 v2
I
C.
(*)
2 R2
1
I Rv 2
D.
2
Altre domande
15. Il periodo delle piccole oscillazioni di un pendolo semplice non dipende
A. dall’ampiezza dell’oscillazione (*)
B. dalla lunghezza del filo
C. dalla massa del pendolo (*)
D. dall’accelerazione di gravità
16. Un moto rettilineo (posizione x, velocità v, accelerazione a) è armonico quando l’accelerazione è
A. a = costante
B. a = − kx con k=costante positiva (*)
C. a = −kx 2 con k=costante positiva
D. a = − kv con k=costante positiva
17. Il centro di massa di un sistema di particelle è quel punto individuato dal vettore
m i ri
A.
r=
i
m i ri
i
ri
B.
i
r=
mi
i
mi
C.
i
r=
m i ri
i
m i ri
D.
r=
i
mi
(*)
i
18. La figura rappresenta due carrucole di raggi r1 ed r2 collegate da una cinghia che non scivola su di esse. Se la
carrucola di raggio r1 ha accelerazione angolare α 1 , l’accelerazione angolare dell’altra carrucola vale
A.
α2 =
r1
α 1 (*)
r2
B.
α2 =
r2
α1
r1
C.
α2 =
r1
α1
r1 + r2
D.
α2 =
r1 + r2
α1
r2
r2
r1
19. Un disco orizzontale gira intorno al proprio asse con velocità angolare costante ω . Ad un certo istante un
piccolo frammento di massa m cade verticalmente sul disco e si attacca alla superficie di esso. Il modulo della
velocità angolare del disco:
A. raddoppia
B. rimane invariato
C. aumenta
D. diminuisce (*)
m
20. Un punto materiale si muove di moto rettilineo lungo l’asse x con velocità v = kt con k = 2 2 e t in
s
secondi. Al tempo t = 0 s, il punto materiale si trova nella posizione x o = x (t = 0 ) = 10m ; al tempo t =2s il
punto materiale si trova nella posizione
A. x = 8m
B. x = 10m
C. x = 12m
D. x = 14m (*)
21. Il centro di massa di un sistema costituito dalle masse puntiformi m 1 ed m 2 , con m 2 >> m 1 , poste a distanza
d, si trova:
d
A. sulla congiungente m 1 − m 2 a distanza da m 1
2
d
B. sulla congiungente m 1 − m 2 a distanza da m 1
4
C. sulla congiungente m 1 − m 2 , vicino ad m 1
D. sulla congiungente m 1 − m 2 , vicino ad m 2 (*)
22. Un disco, di massa m e raggio r, partendo da ferma da un’altezza h (vedi figura) rotola lungo una collina il cui
profilo è rappresentato in figura. Quando il disco arriva nel punto più basso A, la velocità del suo CM è (si
trascuri l’attrito dell’aria e l’attrito volvente)
A.
2gh
B.
4
gh (*)
3
C.
1
gh
2
M,r
h
A
1
gh
3
23. Nel moto parabolico di un proiettile lanciato verso l’alto ad un angolo di 45°, nel punto di altezza massima, la
velocità ha
A. componente orizzontale nulla e componente verticale diversa da zero
B. componente orizzontale diversa da zero e componente verticale nulla (*)
C. entrambe le componenti nulle
D. entrambe le componenti diverse da zero
24. Un sassolino viene lanciato verticalmente verso l’alto. Nel punto di altezza massima, il sassolino ha
A. velocità ed accelerazione nulle
B. velocità ed accelerazione diverse da zero
C. velocità nulla ed accelerazione diversa da zero (*)
D. velocità diversa da zero ed accelerazione nulla
25. I tre settori circolari in figura (1,2,3) sono corpi rigidi bidimensionali, omogenei, di uguale massa
(m1 = m 2 = m 3 = m ) e raggio (r1 = r2 = r3 = r ) . Detti I1 , I 2 , I 3 i loro momenti d’inerzia rispetto ad un asse
passante per O ed ortogonale al piano della
2
3
figura si ha
1
A. I1 = 3I 3 , I 2 = 2I 3
D.
B.
C.
D.
I
I3
, I1 = 2
2
3
I
2I 3
, I1 = 2
I1 =
3
3
I1 = I 2 , I 2 = I 3 (*)
r,
m
I1 =
O
r,
m
O
r,
m
Or
26. Il momento angolare di un corpo rigido QUALSIASI che ruota intorno ad un asse con velocità angolare ω è:
A. parallelo all’asse di rotazione
B. parallelo ed equiverso ad ω
C. perpendicolare all’asse di rotazione
D. ha sia una componente parallela che una componente ortogonale all’asse di rotazione (*)
27. Una ruota di raggio R e massa M compie un moto di puro rotolamento su di un piano orizzontale. Il suo centro
di massa si sposta lungo il piano di ∆s . Il lavoro compiuto dalla forza di attrito statico f s durante questo
spostamento vale:
A. L = 0 (*)
B. L = f s ⋅ ∆s
C.
L = Rf s ⋅ ∆s
1
m∆s 2
2
28. Nel corpo rigido di massa M mostrato in figura, sia a la distanza tra un asse passante per il CM ed un asse
parallelo ad esso e passante per A. Siano I CM ed I A i momenti d’inerzia rispetto a
questi assi, si ha:
A. I CM = I A − M 2 a 2
A
CM
a
B. I CM = I A
D.
L=
C.
I CM = I A + Ma 2
D. I CM = I A − Ma 2 (*)
29. Un oggetto viene sollevato da terra fino ad un’altezza di 10 m e poi abbassato
all’altezza di 1m. Per questi due spostamenti, la forza di gravità compie complessivamente un lavoro
A. Nullo
B. Positivo
C. Negativo (*)
D. Di segno dipendente dal cammino seguito
30. Un punto materiale di massa m si muove in un campo di forza centrale. Durante il moto si conserva:
A. la sua velocità
B. la sua quantità di moto
C. il suo momento angolare (*)
D. nessuna quantità fisica
Soluzione
Esercizio n.1
Non essendoci attrito, l’energia meccanica del sistema molla-pallina si conserva. La pallina, che non è legata alla molla,
si stacca dalla molla quando questa raggiunge la posizione di riposo. La velocità con cui la pallina scivola sul tavolo (e
quindi la velocità orizzontale con cui cade) ha modulo:
k
1
1
k ∆x 2 = mv 2 → v =
∆x
m
2
2
Nella direzione orizzontale, la pallina si muove con moto uniforme e nel tempo t = 0.5 s percorre la distanza d = 2.20 m.
Quindi
d = vt =
m d
→ ∆x = 0.1968 m
k t
k
∆x t → ∆x =
m
L’energia potenziale elastica della molla è
1
k ∆x 2 = 9.6796 J
2
mentre la velocità con cui la pallina lascia il tavolo risulta
d
m
v = = 4 .4
t
s
L’altezza del tavolo è la distanza verticale percorsa dalla pallina nel tempo t = 0.5 s:
1
h = gt 2 = 1.225m
2
essendo il moto verticale della pallina uniformemente accelerato con accelerazione g.
Il modulo della velocità v f con cui la pallina tocca terra può essere ottenuto ad esempio utilizzando il principio di
conservazione dell’energia:
E elas =
1
1
k∆x 2 + mgh = mv f2 → v f =
2
2
m
k∆x 2 + 2mgh
= 6.59
s
m
Esercizio n.2
Nell’urto (completamente anelastico) pallottola-blocco si conserva la quantità di moto. Detto v f il modulo della
velocità orizzontale del sistema pallottola-blocco immediatamente dopo l’urto, dalla conservazione della quantità di
moto si ha:
m
vo
mv o = (m + M )v f → v f =
m+M
Nella fase di salita si conserva l’energia meccanica del sistema pallottola-blocco (le forze esterne agenti sul sistema e
che compiono lavoro sono conservative). Quindi
2
1
(m + M )v f2 = (m + M )gh → 1 (m + M ) m v o = (m + M )gh → v o = m + M 2gh = 397.96 m
s
m
m+M
2
2
La velocità del sistema pallottola-blocco nel punto di altezza massima è ovviamente nulla.
Il sistema pallottola-blocco, oscillando, ripassa per la posizione verticale sempre con la stessa energia cinetica
1
(m + M )v f2 e cioè con velocità v f = m v o = 1.98 m .
2
m+M
s
Esercizio n.3
Con riferimento alle forze rappresentate in figura, le equazioni del moto della ruota e del
blocco sono:
R
RT = Iα
O
−T
mg − T = ma
L’accelerazione a del blocco e l’accelerazione angolare α della ruota sono legate dalla
relazione: a = Rα .
T
Im g
T=
mg
I + mR 2
Risolvendo il sistema si ottiene :
h
R 2 mg
a=
mR 2 + I
Il blocchetto scende con accelerazione costante a, quindi dopo una distanza h, la sua velocità è
v = 2ah =
2R 2 mg
h
mR 2 + I