Argomenti di questa lezione • Ancora esercizi di termodinamica, in

Lezione esTD 30
Argomenti di questa lezione
• Ancora esercizi di termodinamica, in preparazione
della seconda prova in itinere.
pag. 1
Lezione esTD 30
pag. 2
17aprile2003
Una macchina termica è basata su un ciclo reversibile costituito nell’ordine
da una trasformazione isoterma AB in cui il volume aumenta di 4 volte,
una compressione a pressione costante che riporta il gas al suo volume
iniziale e una trasformazione isocora che riporta il gas allo stato iniziale A.
La macchina utilizza 5 moli di gas perfetto monoatomico, e lo stato A (pA,
VA) è noto
Calcolare il lavoro svolto dal gas in ciascuna delle tre trasformazioni:
LAB
LBC
LCA
Calcolare calore scambiato dal gas in ciascuna delle tre trasformazioni:
QAB
QBC
QCA
Calcolare la variazione d’entropia nelle tre trasformazioni :
∆SAB
∆SBC
∆SCA
Determinare il
rendimento del ciclo:
η=
Si supponga ora di sostituire la trasformazione AB con un’espansione
libera adiabatica (mantenendo inalterate tutte le altre cose).
Calcolare lavoro svolto, calore scambiato e variazione d’entropia nella
trasformazione AB e nell’intero ciclo.
LAB
QAB
∆SAB
Lciclo
Qciclo
Riportare sul retro del foglio eventuali commenti.
∆Sciclo
Lezione esTD 30
pag. 3
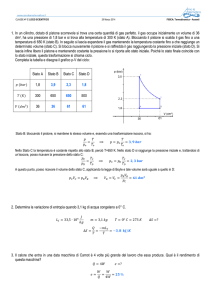
Si consideri un ciclo
termodinamico reversibile che
riguarda n moli di gas perfetto
biatomico e che è costituito
nell’ordine da una compressione
adiabatica AB, da un’isobara BC
e da un’isocora CA. Nella
trasformazione AB, il volume del
gas dimezza.
Determinare il rapporto fra le
pressioni negli stati B ed A e rappresentare il ciclo sul piano pV. Inoltre,
supponendo note la pressione pA e il volume VA dello stato A, calcolare
il lavoro svolto dal gas in AB, il calore scambiato in BC, la variazione
d’entropia in CA, ed il rendimento del ciclo (specificando il tipo di
macchina cui si fa riferimento)
pB/pA
lavoro svolto in AB
calore scambiato nell’isobara
variazione d’entropia
nell’isocora
rendimento del ciclo
O motore
O frigorifero
O pompa di calore
Lezione esTD 30
pag. 4
Del gas perfetto monoatomico (5 moli) subisce un ciclo reversibile
che è costituito da un riscaldamento a volume costante AB, da
un’espansione isobara BC e da una trasformazione CA
caratterizzata dal fatto che ogni variazione di pressione ∆p è
proporzionale alla corrispondente variazione di volume ∆V: cioè
in CA si ha dp/dV=costante. È noto lo stato A (pressione pA,
volume VA) e sono note le quantità di calore scambiate
nell’isocora e nell’isobara. In particolare, QAB=2Q0 e QBC=Q0.
Rappresentare il ciclo sul piano di Clapeyron.
Riempire la seguente tabella con le opportune quantità,
esprimendole in funzione dei dati del problema numero di moli,
pA, VA, e Q0, e della costante dei gas R.
Temperatura
Pressione
Volume
Stato A
pA
VA
Stato B
Stato C
Lezione esTD 30
pag. 5
20020411
Esercizio 3
Una mole di gas perfetto
p0, T0
biatomico a temperatura T0 e
1 mole, T0
S
pressione p0 è contenuta in una
parte di un cilindro il quale ha
sezione di area S ed è diviso a
metà da un setto. L’altra metà del cilindro è vuota.
All’esterno è presente aria alla pressione atmosferica p0 e
alla temperatura T0.
Ad un certo istante, il setto si rompe e si raggiunge un
nuovo equilibrio senza che vi siano scambi di calore con
l’esterno; poi per mezzo di un pistone, sempre impedendo
che ci siano scambi di calore, il gas viene riportato
lentamente al suo volume iniziale. Adesso, viene bloccato il
pistone e si permette al gas di scambiare calore con
l’esterno, fino a raggiungere l’equilibrio termico.
a) Rappresentare (ove possibile) le varie fasi del processo
sul piano di Clapeyron.
b) Calcolare la forza con cui deve essere tenuto il pistone
prima che si rompa il setto, dopo il primo equilibrio,
dopo la compressione e dopo l’equilibrio termico.
c) Calcolare l'integrale di Clausius e la variazione
dell’entropia del gas nelle diverse fasi, nonché la
variazione totale.
d) Calcolare il lavoro fatto in ciascuna fase dal gas
contenuto nel cilindro.
Lezione esTD 30
pag. 6
20040402 Esercizio 3
Del gas perfetto biatomico subisce un ciclo reversibile ABC
costituito nell’ordine da un’espansione isobara AB, una
compressione isoterma BC ed una trasformazione isocora CA. Si
conosce lo stato A (pA, VA, TA) del gas, inoltre si sa che
nell’isobara viene scambiata una quantità di calore Q. Calcolare
a) il calore scambiato nell’isocora;
b) il lavoro svolto in un ciclo;
c) la variazione d’entropia in ciascuna tre trasformazioni;
d) il rendimento del ciclo dopo aver dichiarato di tipo di macchina
termica cui si fa riferimento.
Lezione esTD 30
pag. 7
20040402 Esercizio 3
3a) Sfruttando il fatto che, per definizione di cp, nelle
isobare Q=ncp∆T, si può determinare la variazione di
temperatura in AB, e così si può ricavare TBC=TA+Q/ncp.
Poiché pB e VC sono noti (e uguali rispettivamente a pA e
VA) la conoscenza della temperatura TBC permette di
determinare univocamente gli stati B e C.
3b) E’ ora possibile determinare il lavoro svolto
nell’isoterma (che per il 1° principio della termodinamica
applicato ai gas perfetti nelle isoterme è uguale al calore
scambiato), infatti
LBC=∫pdV=nRTBC∫VBVCdV/V=nRTBCln(VC/VB)=
nR(TBC)ln(VA/VB)=
nR(TBC)ln(TA/TB)=
nR(TBC)ln[TA/(TA+Q/ncp)],
quantità negativa (è <1 l’argomento del logaritmo) poiché
si tratta di calore ceduto.
Il lavoro svolto nel ciclo può essere calcolato come
LBC+LAB, oppure, sfruttando il fatto che in un ciclo
Ltot=Qass−Qced, si può trovare come
QAB+QBC+QCA=Q+QBC+ncV∆TCA=
Q+nR(TA+Q/ncp)ln[TA/(TA+Q/ncp)]−cVQ/cp.
Lezione esTD 30
pag. 8
3c) Trattandosi di tre trasformazioni reversibili, le
variazioni d’entropia si possono direttamente valutare
attraverso integrali di Clausius:
∆SAB=∫ABdQ/T=ncpln(TB/TA)=ncpln[(TA+Q/ncp)/TA),
∆SBC=∫BCdQ/T=∫BCdL/T=∫BCpdV/T= ∫BC(nRT/V)dV/T=
nRln(VC/VB)=nRln(VA/VB)=nRln(TA/TB)=
nRln[TA/(TA+Q/ncp)], e similmente ∆SCA=
ncVln[TA/(TA+Q/ncp)].
E’ utile ed opportuno verificare che la somma delle tre
variazioni sia nulla, come deve essere in ogni ciclo.
3d) Il ciclo viene percorso in senso antiorario, per cui può
descrivere un frigorifero (e allora
η=ηfrigo=Qass/|L|=QAB/|L|=Q/|L|) o una pompa di calore (nel
qual caso η=ηpc=Qced/L=(Qass+|L|)/|L|=1+ηfrigo).
Lezione esTD 30
20040402 Esercizio 4
pag. 9
pA
VA
TA
Un cilindro è diviso in
due parti da un setto.
Le due parti hanno volume diverso: una lo ha triplo
dell’altra. Inizialmente, nella parte più piccola è presente
del gas in uno stato A (pA, VA, TA) noto, mentre la parte più
grande è vuota.
Improvvisamente, il setto si rompe così che il gas può
andare ad occupare tutto il cilindro; si indichi con B lo stato
d’equilibrio raggiunto al termine di questo processo. A
questo punto, per mezzo di un pistone il gas viene
compresso lentamente e senza consentire scambi di calore.
Tale compressione procede fin quando la pressione del gas
raggiunge il valore iniziale pA; si indichi C lo stato finale.
Descrivere l’intero processo con un grafico sul piano pV.
Calcolare l’integrale di Clausius e la variazione d’entropia
nelle due trasformazioni AB e BC. Determinare inoltre la
temperatura dello stato C ed il lavoro necessario per
ricomprimere il gas fino allo stato C.
Lezione esTD 30
pag. 10
20040402 Esercizio 4
Alla rottura del setto, si verifica un’espansione libera molto
rapida (perciò si può ritenere che sia trascurabile ogni
scambio di calore).
Dunque, avviene un processo senza scambio di calore nel
quale non viene compiuto lavoro né dal gas né sul gas. Per
il primo principio della termodinamica, da ciò si deduce che
l’energia interna del gas resta costante.
Trattandosi di gas perfetti, ∆Eint=0 implica ∆T=0, perciò
possiamo concludere che TB=TA.
In questo processo , che è palesemente irreversibile,
l’integrale di Clausius è nullo. Vista l’irreversibilità, la
variazione d’entropia deve essere quindi >0.
Per calcolarla, possiamo valutare l’integrale di Clausius su
un’altra trasformazione (che sia reversibile) la quale porti
da A a B.
In particolare, visto che abbiamo appena asserito che
TC=TA, possiamo calcolarlo su un’isoterma reversibile, e
così otteniamo
∆SAB=∫ABdQ/T=∫ABdL/T=∫ABpdV/T= ∫AB(nRT/V)dV/T=
nRln(VB/VA)∆SAB=nRln4.
Lezione esTD 30
pag. 11
Vale la pena fare una considerazione sul segno di questa
quantità: perché questa variazione d’entropia è sicuramente
positiva?
Notiamo che lo è perché l’argomento del logaritmo è >1,
ovvero perché il volume finale è maggiore di quello
iniziale… Come dire che, spontaneamente, un gas può
espandersi ad occupare un volume maggiore ma non si
contrarrà mai per andare ad occupare un volume minore.
Dopo l’espansione libera, il gas viene ricompresso con un
processo adiabatico e reversibile fino a raggiungere
nuovament la pressione pA.
Nelle adiabatiche reversibili, pVγ=costante, inoltre come
sempre per i gas perfetti pV=nRT, dividendo queste due
relazioni membro a membro dopo aver elevato ad 1/γ la
prima, otteniamo p(1/γ−1)T=costante, che per un gas
monoatomico dà p−2/5T=costante.
Poiché lo stato B, avendo la stessa temperatura di A e
volume quadruplo è a pressione pA/4, possiamo asserire che
deve essere
pB−2/5TB= (pA/4)−2/5TA=pC−2/5TC=pA−2/5TC
da cui TC=TA42/5.
Il lavoro svolto sul gas nell’adiabatica reversibile BC è pari
alla variazione d’energia
Lezione esTD 30
pag. 12
170306
170306 Esercizio 1
Un ciclo termodinamico reversibile riguarda del gas
monoatomico ed è costituito, nell’ordine, da un’espansione
isoterma, un’espansione adiabatica, una compressione
isobara ed un’isocora. È noto lo stato A del gas (pA, TA,
VA), che è quello a temperatura massima. Inoltre si sa che
in ciascuna delle due espansioni la pressione dimezza.
Dopo aver rappresentato (sul retro del foglio) l’intero
processo sul piano pV, calcolare
a) il lavoro svolto nell’adiabatica
b) il lavoro svolto in un ciclo
c) il calore scambiato in ciascuna trasformazione
d) la variazione d’entropia del gas in ciascuna
trasformazione
e) il rendimento del ciclo
il rendimento che avrebbe una macchina di Carnot
funzionante fra le temperature massima e minima raggiunte
da questa macchina durante il ciclo.
Ladiab
Lciclo
∆SAB
∆SBC
∆SCD
∆SDA
η
QAB
QBC
QCD
QDA
ηCarnot
Lezione esTD 30
pag. 13
170306 Esercizio 2
Si hanno n moli di gas
monoatomico contenute in un
volume limitato da un pistone di
peso trascurabile a tenuta perfetta,
il quale può scorrere senza attriti
in un intervallo limitato di
gas monoatomico
n moli
posizioni (vedi figura).
All’esterno del contenitore è
presente l’atmosfera a pressione
p0, che quindi si esercita sulla
superficie superiore del pistone.
Inizialmente, il gas è a
temperatura T0 ed occupa il volume minimo (il pistone
tocca inferiormente), poiché la sua pressione è p0/2. Viene
fornito calore Q fino a quando il pistone inizia a staccarsi
dal supporto inferiore. Poi viene fornito altrettanto calore Q
e si osserva che il pistone sale fino a toccare superiormente.
Viene fornita per la terza volta una quantità di calore Q.
Infine, il sistema viene isolato termicamente, e viene
applicata una forza esterna sul pistone tale da farlo tornare
alla sua posizione iniziale. Rappresentare (sul retro del
foglio) l’intero processo sul piano di Clapeyron. Calcolare
la temperatura e la pressione finale del gas e la variazione
d’entropia in ogni fase del processo.
p0
T
p
∆S
∆S
∆S
∆S
Lezione esTD 30
pag. 14
170306Esercizio 3
Un inventore dichiara di aver costruito una macchina
termica ciclica che lavora scambiando calore fra due
termostati che hanno rispettivamente temperatura T1=127°C
e T2=327°C. L’inventore afferma che, in ogni ciclo, tale
macchina scambia con la sorgente fredda una quantità di
calore Q1=4kJ e con la sorgente calda una quantità di calore
Q2<7kJ, producendo una quantità di lavoro L. Determinare
qual è il valore massimo che può assumere L sulla base del
primo e del secondo principio della termodinamica,
chiarendo quindi se è plausibile che l’inventore fornisca il
dato L=2.5kJ
In base al 1° principio, Lmax =
In base al 2° principio, Lmax =
Quindi il dato di L fornito dall’inventore…
è plausibile
non è plausibile
Lezione esTD 30
pag. 15
060324 Esercizio 1
Un ciclo termodinamico reversibile riguarda del gas monoatomico
ed è costituito, nell’ordine, da un’espansione adiabatica,
un’espansione isoterma, una compressione isobara ed un’isocora.
È noto lo stato A del gas (pA, TA, VA), che è quello a temperatura
massima. Inoltre si sa che in ciascuna delle due espansioni il
volume raddoppia. Dopo aver
rappresentato l’intero processo sul piano
pV, calcolare
a) il lavoro svolto nell’isoterma
b) il calore scambiato isocora
c) la variazione d’entropia del gas
nell’isobara
d) il rendimento del ciclo
e) il rendimento che avrebbe una
macchina di Carnot funzionante fra le temperature massima e
minima raggiunte da questa macchina durante il ciclo.
NB:si chiede di esprimere i risultati solo in termini di pA, TA, VA
L
∆S
Q
η
ηCarnot
Lezione esTD 30
pag. 16
060324 Esercizio 2
Un inventore di nome Carletto dichiara di aver costruito una
macchina termica ciclica che produce lavoro scambiando calore
fra due termostati che hanno rispettivamente temperatura
T1=−30°C e T2=300°C. Egli afferma che tale macchina scambia
calore con la sorgente fredda ad una potenza termica di 1.0kW e
sviluppa una potenza meccanica non inferiore a 800W.
Determinare se quanto asserito da Carletto è compatibile con i
principi della termodinamica, e, in caso affermativo indicare in
quale intervallo di valori deve essere la potenza termica assorbita
Non è compatibile perché…
È compatibile, e la potenza termica assorbita è nell’intervallo fra…
Pass-min =
Pass-max =