Ottica geometrica

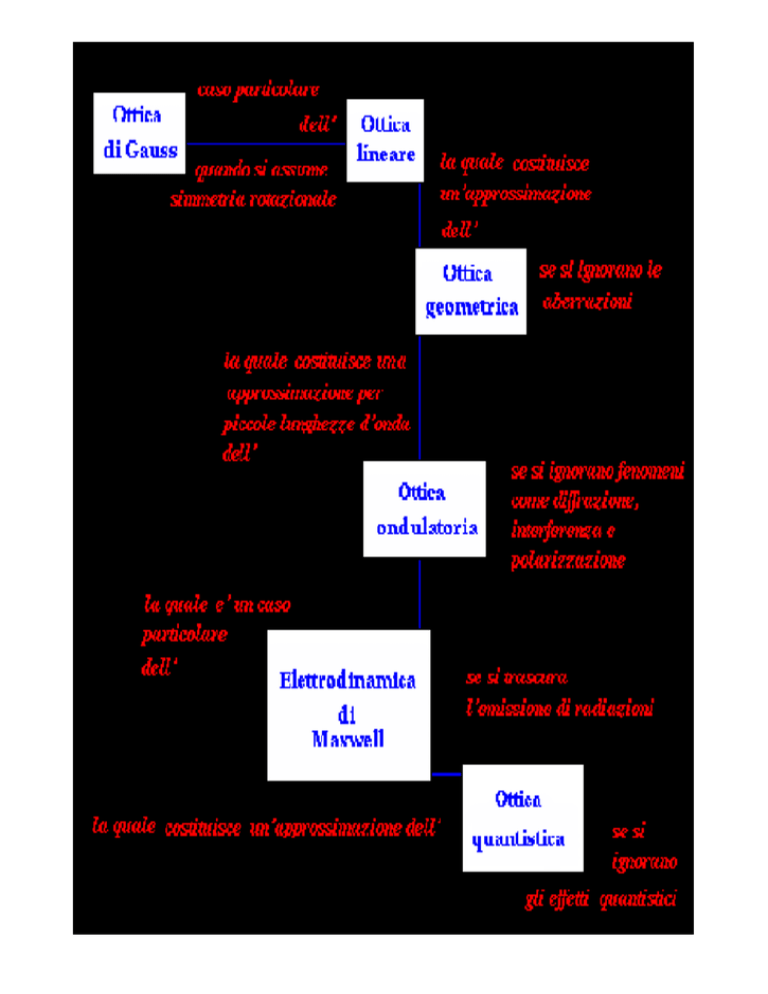
OTTICA GEOMETRICA
L'Ottica Geometrica studia le leggi dei raggi,
schematizzandoli in rette geometriche
Le leggi dell'ottica geometrica
Tutti i fenomeni luminosi trovano rigorosa
spiegazione nella teoria elettromagnetica della
luce. Tuttavia lo studio della propagazione della
luce, considerata come fenomeno
elettromagnetico, presenta notevoli difficoltà
analitiche. Si impiegano allora metodi
approssimati capaci di prevedere l'andamento di
quasi tutti i fenomeni che si presentano nella
pratica con sufficiente previsione. Questi
metodi sono basati su leggi sperimentali
scoperte prima della formulazione della teoria
elettromagnetica della luce.
Fra questi metodi approssimati rientra l'Ottica
geometrica, la quale studia il comportamento di
fenomeni semplici interpretati mediante leggi di
carattere geometrico.
L'ottica geometrica è governata da quattro leggi
fondamentali:
Ø propagazione rettilinea della luce
Ø indipendenza dei raggi luminosi
Ø riflessione della luce su una superficie
speculare
Ø rifrazione della luce sulla superficie di
separazione fra due mezzi trasparenti.
Ø
Propagazione rettilinea della luce in
un mezzo omogeneo
Si rivela molto utile considerare i raggi
luminosi come delle semplici rette. Si tratta di
un'astrazione matematica, scelta per facilitare i
ragionamenti e tale da permettere una chiara
rappresentazione dei fenomeni e dei dispositivi
sperimentali: le rette geometriche, a differenza
dei raggi luminosi, non hanno spessore.
Ø Indipendenza dei raggi luminosi
Quando due o più raggi si intersecano non si
verifica alcuna alterazione di traiettoria o
intensità.
Ø Riflessione della luce su una superficie
speculare
Le leggi della riflessione nel linguaggio
geometrico sono descritte come segue:
1.Il raggio incidente, il raggio riflesso e la
perpendicolare (normale) alla superficie
riflettente nel punto d'incidenza, giacciono sul
medesimo piano.
2.L'angolo di riflessione è uguale
all'angolo di incidenza: i=r.
Se il raggio incidente coincide con la normale
allo specchio, formando un angolo di incidenza
uguale a zero, anche il raggio riflesso forma un
angolo di riflessione nullo: coincide con il
raggio incidente (incidenza normale).
Queste leggi valgono anche se la superficie è
curva. In questo caso la normale nel punto
d'incidenza è la perpendicolare al piano
tangente alla superficie stessa in quel punto.
Quando la superficie è sferica la normale in un
punto coincide con il raggio della sfera
(passante per quel punto)
Ø Rifrazione della luce sulla superficie
di separazione fra due mezzi trasparenti.
Quando un fascio di raggi luminosi incontra
la superficie di separazione di due mezzi
trasparenti, in parte si riflette e in parte
prosegue nel nuovo mezzo.
La rifrazione è regolata dalle seguenti leggi:
1.raggio incidente, raggio rifratto e
normale nel punto d'incidenza alla superficie
di separazione dei due mezzi giacciono sullo
stesso piano.
2.Il rapporto tra i seni degli angoli che il
raggio incidente ed il raggio rifratto formano
con la normale è una costante che dipende
dalla natura dei due mezzi, dalle loro
condizioni fisiche (temperatura, pressione,
stato di aggregazione) e dalla lunghezza
d'onda della luce utilizzata. Tale costante è
denominata indice di rifrazione del secondo
mezzo rispetto al primo.
sin (i )
n =
sin ( r ' )
12
Se l'angolo di rifrazione è minore di quello di
incidenza si dice che il secondo mezzo (es.
acqua) è più rifrangente del primo (es. aria); se
invece l'angolo di rifrazione è maggiore di
quello d'incidenza, il secondo mezzo è meno
rifrangente del primo. In generale i mezzi più
densi sono anche più rifrangenti. Può tuttavia
avvenire anche il contrario: l'alcol, il petrolio, la
benzina, pur essendo meno densi dell'aria sono
più rifrangenti di essa.
Le leggi della rifrazione, nella forma
geometrica, si dicono anche leggi di Cartesio,
perché furono pubblicate per la prima volta da
Descartes nel 1637, pur essendo state scoperte
nel 1615 dall'olandese W. Snell.
Angolo limite
Dati due mezzi rifrangenti, consideriamo una
sorgente di luce in quello meno rifrangente e
facciamo variare l'angolo d'incidenza da 0 a 90
gradi. Se l'angolo d'incidenza è zero, anche
l'angolo di rifrazione deve essere zero. Se un
raggio di luce incontra normalmente la
superficie di separazione dei due mezzi,
prosegue nella stessa direzione, cioè si rifrange
senza deviare. Crescendo l'angolo di incidenza
cresce l'angolo di rifrazione, pur mantenendosi
sempre minore. Quando l'angolo di incidenza
ha raggiunto il valore massimo di 90 gradi, che
si ha quando il raggio incidente è radente alla
superficie di separazione, anche l'angolo di
rifrazione ha raggiunto il valore massimo.
Questo valore massimo dell'angolo di rifrazione
si chiama angolo limite.
L'angolo limite è il valore dell'angolo di
rifrazione corrispondente ad un angolo
d'incidenza di 90 gradi, quando il raggio passa
da un mezzo meno rifrangente ad uno più
rifrangente.
Riflessione totale
Dati due mezzi rifrangenti, consideriamo una
sorgente di luce in quello più rifrangente e
facciamo variare l'angolo d'incidenza. Finché il
raggio incidente è compreso nell'angolo limite
se ne trova il raggio rifratto corrispondente nel
mezzo meno rifrangente; ma se il raggio
incidente è esterno all'angolo limite, non
avendosi piu’ il corrispondente raggio rifratto,
non uscirà nel mezzo meno rifrangente, ma si
rifletterà totalmente come se la superficie di
separazione dei due mezzi fosse speculare.
Pertanto: un raggio si può sempre rifrangere
quando passa da un mezzo ad un altro più
rifrangente, ma se l'angolo d'incidenza è
superiore all'angolo limite, non si rifrange più
ma dà luogo al fenomeno della riflessione totale
con le stesse leggi della riflessione.
n12
sin ( 90 )
1
=
=
sin ( r 'lim ) sin ( r 'lim )
sin ( r ' lim
1
)=
n12
Rifrazione attraverso lastre
Viene denominato lastra un mezzo trasparente
delimitato da facce piane e parallele.
Tipicamente le lastrine di vetro su cui si
eseguono strisci o preparazioni per osservazione
ad esempio al microscopio ottico composto.
Un raggio SI, incidendo obliquamente sulla
lastra MM', si rifrange secondo II'. Il raggio
rifratto II' forma con le normali N e N', tra loro
parallele, angoli interni uguali: r=r'. All'uscita
nell'aria si dovrà quindi verificare la
condizione: i=i'. Pertanto il raggio emergente
I'S' è parallelo al raggio incidente SI.
Dunque:Un raggio che attraversa una lastra non
è deviato dalla sua direzione. Esso è spostato
parallelamente a se stesso: lo spostamento è
proporzionale allo spessore della lastra e
all'angolo d'incidenza.
DISPERSIONE DELLA LUCE
Il Prisma Ottico
Il prisma ottico è un mezzo rifrangente limitato
da facce piane non parallele formanti cioè un
angolo diedro, detto "angolo del prisma".
Sia A l'angolo del prisma e SI un raggio
incidente. Quando un raggio proveniente
dall'aria incide sul prisma (nel punto d'incidenza
I), attraversa un mezzo più rifrangente (vetro),
quindi il raggio si avvicina alla normale n1;
quando poi giunge nel punto E emerge dal
prisma (a meno di superare l'angolo limite) in
un mezzo meno rifrangente, l'aria, quindi il
raggio si avvicina alla normale n2 lungo la
direzione ER. Per effetto delle due rifrazioni il
raggio devia verso la base BC.
L'angolo formato dal prolungamento del raggio
emergente EO con il prolungamento del raggio
incidente OF, è detto angolo di deviazione del
prisma.
Per ogni prisma vi è un angolo minimo di
deviazione: si ottiene quando l'angolo
d'incidenza e l'angolo di emergenza sono
uguali. Uno stesso materiale presenta indici di
rifrazione diversi per i vari colori.
STRUMENTI OTTICI
Ø Riflessione (Specchi piani e sferici)
Ø Rifrazione(Lenti, Prismi etc.)
Lente:
Ø Diottro è Lente ad una sola superfice
separante due mezzi di differente indice di
rifrazione.
Ø Lenti è Insiemi di piu’ diottri
Specchi
COSTRUZIONE IMMAGINE
Ø L’asse ottico di uno specchio e’ individuato
dalla retta passante per il fuoco ed il centro di
curvatura dello specchio
Ø Raggio parallelo all’asse ottico passa per il
fuoco.
Ø Raggio per il centro di curvatura dello
specchio si riflette ripassando verso il centro
di curvatura
Ø Raggio passante per il fuoco si riflette
parallelo all’asse ottico.
Le Lenti
L’elemento piu’ semplice che divide due mezzi
di differenti indici di rifrazione si chiama
diottro sferico.
Eseguendo lo stesso tipo di ragionamento fatto
per il caso degli specchi sferici, questa volta
applicato alla rifrazione si ottiene la seguente
relazione, che costituisce la formula dei punti
coniugati per il diottro sferico:
n1 n2 n2 − n1
+ =
p q
R
La lente è un mezzo trasparente limitato da due
facce ben levigate (diottri) di cui almeno una è
curva. Si tratta della più importante
applicazione del fenomeno della rifrazione.
Secondo la curvatura delle facce, le lenti
possono essere: sferiche, cilindriche,
paraboliche. La trattazione della rifrazione dei
raggi luminosi attraverso una lente risulta, nel
caso generale, molto complessa; ci limitiamo al
caso particolare delle lenti molto sottili (lo
spessore e’ molto piccolo rispetto al raggio di
curvatura) e raggi parassiali (quasi paralleli
all'asse ottico).
Noi ci occuperemo solo delle lenti sferiche,
dividendole in due gruppi: convergenti (quelle
che fanno convergere un fascio di raggi
paralleli) e divergenti (quelle che li fanno
divergere).
Una lente convergente (più grossa al centro
che agli orli) si può pensare ottenuta da una
coppia di prismi riuniti per le basi: i raggi
emergenti, deviando verso le basi,sono portati a
convergere.
Una lente divergente (più grossa agli orli che
al centro) ricorda una coppia di prismi riuniti
per gli spigoli: i raggi emergenti emergono
deviando verso le basi. Sia le lenti convergenti
che le divergenti si possono classificare in tre
tipi: biconvessa, piano-convessa, concavoconvessa ( menisco convergente), biconcava,
piano-concava, convesso-concava (menisco
divergente).
Convergenti: 1) biconvessa, 2) piano-convessa,
3) concavo-convessa
Divergenti: 4) biconcava, 5) piano-concava, 6)
convesso-concava
Si chiama asse ottico principale la retta
congiungente i centri delle superfici sferiche
che delimitano la lente; nel caso di lenti pianosferiche coincide con la retta
passante per il centro della superficie sferica e
perpendicolare alla superficie piana. Si chiama
asse secondario ogni retta passante per il centro
ottico.
È denominato centro ottico il punto dell'asse
ottico della lente sottile che gode della
proprietà di non deviare le radiazioni luminose
passanti per esso. Il centro divide il
segmento congiungente i centri di curvatura in
parti direttamente proporzionali ai raggi.
Il fuoco di una lente F1 è il punto dell'asse
ottico principale nel quale convergono i raggi di
un fascio monocromatico, parallelo al
medesimo asse, dopo aver inciso sulla lente.
Si chiama distanza focale la distanza del fuoco
dal centro della lente.La distanza focale è
l'elemento più importante tra le
caratteristiche una lente; esso dipende dai
raggi di curvatura delle due facce e dall'indice
di rifrazione del materiale.Nel caso della lente
convergente il fuoco è situato dalla parte
opposta rispetto al fascio incidente. La distanza
focale è espressa da un numero positivo.
Il fuoco delle lenti divergenti è situato dalla
stessa parte dalla quale proviene il fascio
incidente. Si tratta di un fuoco virtuale: trae
origine dal prolungamento dei raggi rifratti
uscenti dalla lente. La distanza focale risulta
espressa da un numero negativo.
Costruzione grafica delle immagini
Per costruire graficamente l'immagine di un
punto si utilizzano due raggi particolari dei
quali è facile prevedere il cammino dopo la
rifrazione:
1.il raggio parallelo all'asse ottico: in seguito
alla rifrazione passa per il fuoco della lente
2.il raggio che attraversa la lente passando
per il suo centro: in seguito alla rifrazione
non subisce deviazione.
3.il raggio che passa per il fuoco e’ rifratto
dalla lente parallelo all’asse ottico
Usando questi raggi a percorso noto è possibile
costruire immagini di oggetti estesi
individuandone i punti principali.
Per le lenti convergenti vale la formula dei
punti coniugati
1 1 1
+ =
p q f
1 1 1
1 1
+ = (n −1) −  =
p q
 R1 R2  f
I raggi di curvatura Ri dei diottri costituenti la
lente per convenzione hanno segno + o segno –
a seconda che la convessita’ del diottro sia
rivolta verso la direzione di provenienza della
luce (+) o in direzione opposta (-).
Per le lenti divergenti si applica la stessa legge f
e q sono espresse da numeri negativi, in quanto
l'immagine è sempre virtuale.
Potere Diottrico o Potenza di una lente
Si definisce potere diottrico o potenza di una
lente l’inverso della distanza focale della lente
espressa in metri :
P =
1
f metri
−1
P
=
m
=>
Diottrie
Esempi: f = 20 cm = + 0.2 m
P = +5 D
f = -20 cm = - 0.2 m
P = -5 D