Esercizio #1
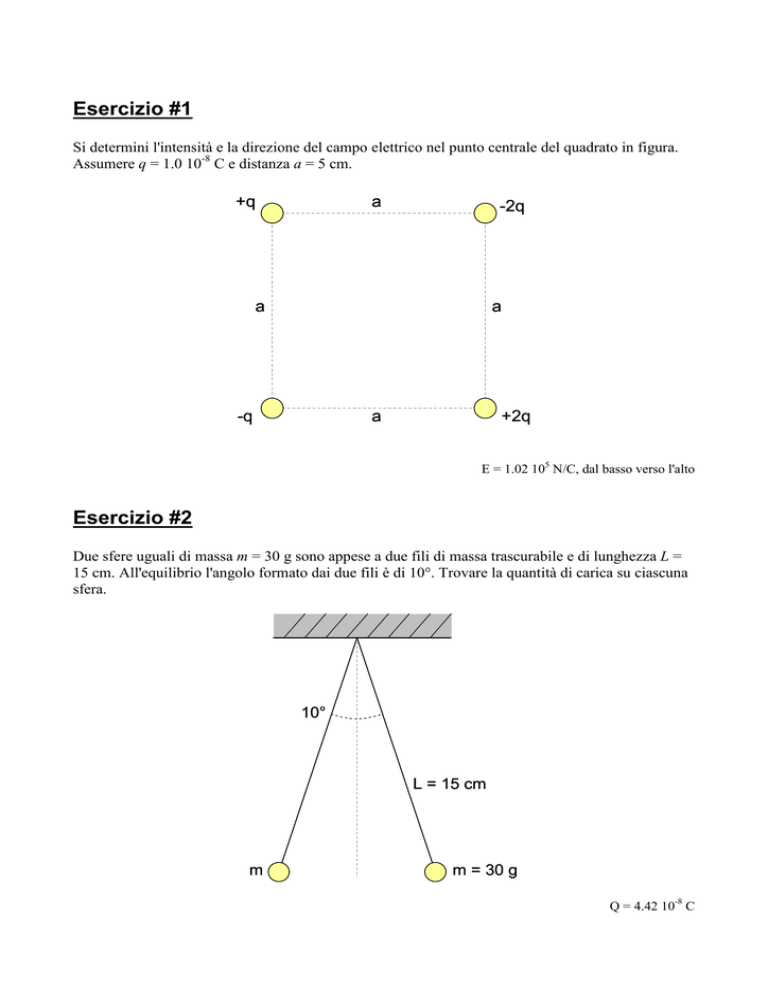
Si determini l'intensità e la direzione del campo elettrico nel punto centrale del quadrato in figura.
Assumere q = 1.0 10-8 C e distanza a = 5 cm.
+q
a
-2q
a
a
-q
a
+2q
E = 1.02 105 N/C, dal basso verso l'alto
Esercizio #2
Due sfere uguali di massa m = 30 g sono appese a due fili di massa trascurabile e di lunghezza L =
15 cm. All'equilibrio l'angolo formato dai due fili è di 10°. Trovare la quantità di carica su ciascuna
sfera.
10°
L = 15 cm
m
m = 30 g
Q = 4.42 10-8 C
Esercizio #3
Un asta di materiale isolante di massa trascurabile, imperniata al centro, è bilanciata da un peso di
massa m = 10 g posta a distanza x dall'estremo sinistro dell'asta (vedi figura). Alle estremità sono
poste due cariche puntiformi rispettivamente di valore q = 1 nC e 2q = 2 nC. Sotto ciascuna delle
due cariche è posta una carica Q a distanza h = 2 cm.
a) Calcolare la distanza x a cui appendere la massa m affinché l'asta sia in equilibrio orizzontale;
b) Quale dovrebbe essere la distanza h affinché il perno non eserciti alcuna forza verticale quando
l'asta è bilanciata e orizzontale?
x
+q
+2q
Lasta = 1 m
h
h
m = 10 g
+Q
+Q
(a) x = 61.5 cm (b) h = 1.66 cm
Esercizio #4
Le gocce di inchiostro espulse dal serbatoio di una cartuccia di una stampante sono caricate,
mediante l'unità di carica, con una carica negativa Q = 1.5 10-13 C. Quando la goccia di massa m =
1.3 10-10 Kg entra tra i piatti del circuito di deflessione ha una velocità parallela ai piatti V0x = 18
m/s. La lunghezza dei piatti è di 1.6 cm e, essendo carichi con carica opposta, generano un campo
elettrico uniforme E rivolto verso il basso con intensità di 1.4 106 N/C.
Qual'è la deflessione verticale ∆y della goccia in corrispondenza dell'estremità all'uscita dai piatti?
Unità di
carica
Piatti di deflessione
Serbatoio
inchiostro
+ + + + + + + + + + + + +
y
∆y
V0x
0
x
E
- - - - - - - - - - - - - - - L = 1.6 cm
∆y = 0.64 mm
Esercizio #5
Un campo elettrico uniforme E ha intensità di modulo 2K N/C ed è diretto e orientato lungo l’asse x.
Una carica puntiforme Q = 3 µC è posta nell’origine ed è libera di muoversi.
a) Calcolare l’energia cinetica della carica Q quando si trova in posizione x = 4 m;
b) Quanto vale la variazione di energia potenziale elettrica della carica da x = 0 m a x = 4 m?
c) Quanto vale la differenza di potenziale V(4 m) – V(0 m)?
Trovare il potenziale V(x) nel caso in cui:
d) V(0) = 0 V
e) V(0) = 4K V
f) V(1) = 0 V
(a) Ecin = 2.4 10-2 J
(b) ∆U = -2.4 10-2 J
(c) ∆V = -8000 V
(d) V(x) = -2000 x V
(e) V(x) = -2000 x + 4000 V
(f) V(x) = -2000 x + 2000 V
Esercizio #6
L’intensità di un campo elettrico uniforme è diretta e orientata nella direzione negativa dell’asse x. I
punti a e b giacciono sull’asse x rispettivamente in x(a) = 2 m e x(b) = 6 m.
a) La differenza di potenziale V(b) – V(a) è positiva o negativa?
b) Se il valore assoluto di V(b) – V(a) è 105 V, quanto vale il modulo del campo elettrico E?
(a) positiva
(b) E = 25 103 V/m
Esercizio #7
Tre cariche puntiformi Q1, Q2 e Q3 sono poste nei vertici di un triangolo equilatero di lato 2.5 m. Si
trovi l’energia potenziale elettrostatica di questa distribuzione di carica se:
a) Q1 = Q2 = Q3 = 4.2 µC
b) Q1 = Q2 = 4.2 µC e Q3 = -4.2 µC
c) Q1 = Q2 = -4.2 µC e Q3 = +4.2 µC
(a) U = 0.190 J
(b) U = -0.0634 J
(c) U = -0.0634 J
Esercizio #8
Tre particelle cariche sono allineate e distanti d come in figura. Le cariche Q1 e Q2 sono mantenute
ferme, mentre le carica Q3, libera di muoversi, è mantenuta in equilibrio dalle forze elettriche.
Determinare il valore di Q1 e la forza elettrica che agisce su di essa, assumendo:
Q2 = 1 nC
Q3 = 2 nC
d = 1 cm.
d
d
Q1
Q2
Q3
Q1 = -4 nC, F = 0.54 mN
Esercizio #9
Due cariche positive uguali Q pari a 2 10-4 C sono fissate rispettivamente nei punti A(1 m, 0 m) e
B(-1 m, 0 m) di un sistema di assi cartesiani x, y. Calcolare:
a) Modulo, direzione e verso della forza che agisce su una carica positiva q = 10-6 C che si
trova nel punto P(0 m, 1 m)
b) Il lavoro che le forze del campo elettrico compiono quando la carica q viene spostata da P a
R(0 m, 2 m)
y (m)
R(0, 2)
P(0, 1)
x (m)
B(-1, 0)
A(1, 0)
(a) F = 1.27 N diretta verticalmente verso l'alto
(b) L = -0.94 J












