Elettronica dello Stato Solido
6.2.2013
1. Si consideri un cristallo con reticolo cubico semplice. La distanza interatomica vale a = 0.34 nm. Si disegni un piano di indici
(2,1,0) e si calcoli la minima distanza tra due di questi piani adiacenti.
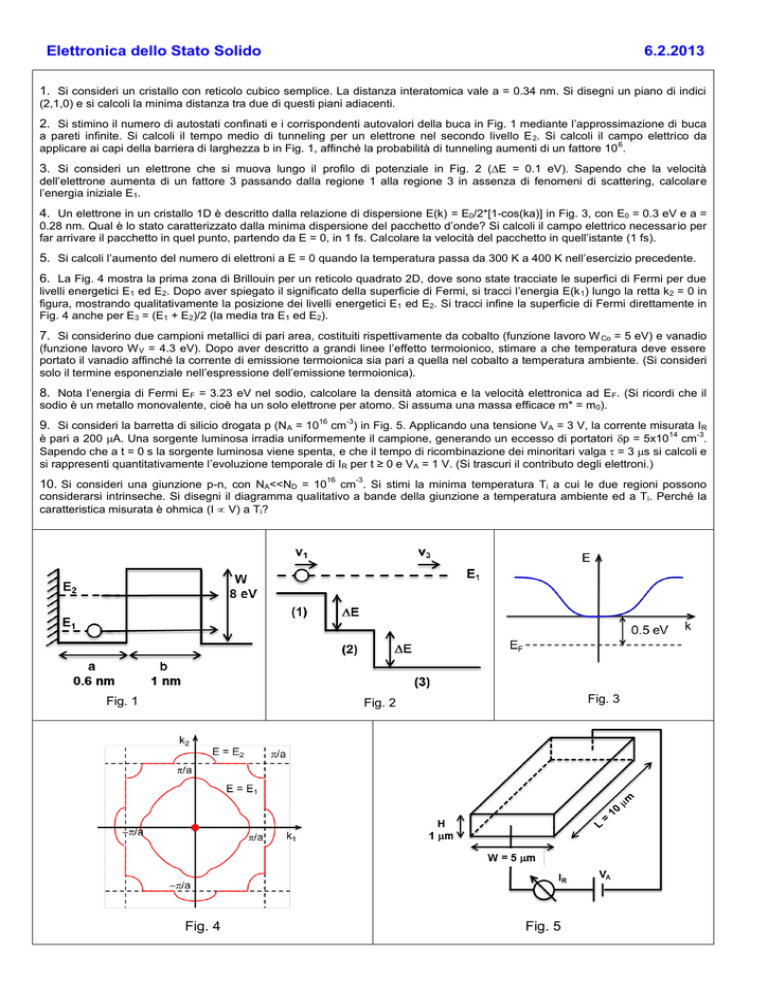
2. Si stimino il numero di autostati confinati e i corrispondenti autovalori della buca in Fig. 1 mediante l’approssimazione di buca
a pareti infinite. Si calcoli il tempo medio di tunneling per un elettrone nel secondo livello E 2. Si calcoli il campo elettrico da
6
applicare ai capi della barriera di larghezza b in Fig. 1, affinché la probabilità di tunneling aumenti di un fattore 10 .
3. Si consideri un elettrone che si muova lungo il profilo di potenziale in Fig. 2 (E = 0.1 eV). Sapendo che la velocità
dell’elettrone aumenta di un fattore 3 passando dalla regione 1 alla regione 3 in assenza di fenomeni di scattering, calcolare
l’energia iniziale E1.
4. Un elettrone in un cristallo 1D è descritto dalla relazione di dispersione E(k) = E0/2*[1-cos(ka)] in Fig. 3, con E0 = 0.3 eV e a =
0.28 nm. Qual è lo stato caratterizzato dalla minima dispersione del pacchetto d’onde? Si calcoli il campo elettrico necessario per
far arrivare il pacchetto in quel punto, partendo da E = 0, in 1 fs. Calcolare la velocità del pacchetto in quell’istante (1 fs).
5. Si calcoli l’aumento del numero di elettroni a E = 0 quando la temperatura passa da 300 K a 400 K nell’esercizio precedente.
6. La Fig. 4 mostra la prima zona di Brillouin per un reticolo quadrato 2D, dove sono state tracciate le superfici di Fermi per due
livelli energetici E1 ed E2. Dopo aver spiegato il significato della superficie di Fermi, si tracci l’energia E(k 1) lungo la retta k2 = 0 in
figura, mostrando qualitativamente la posizione dei livelli energetici E1 ed E2. Si tracci infine la superficie di Fermi direttamente in
Fig. 4 anche per E3 = (E1 + E2)/2 (la media tra E1 ed E2).
7. Si considerino due campioni metallici di pari area, costituiti rispettivamente da cobalto (funzione lavoro W Co = 5 eV) e vanadio
(funzione lavoro W V = 4.3 eV). Dopo aver descritto a grandi linee l’effetto termoionico, stimare a che temperatura deve essere
portato il vanadio affinché la corrente di emissione termoionica sia pari a quella nel cobalto a temperatura ambiente. (Si consideri
solo il termine esponenziale nell’espressione dell’emissione termoionica).
8. Nota l’energia di Fermi EF = 3.23 eV nel sodio, calcolare la densità atomica e la velocità elettronica ad E F. (Si ricordi che il
sodio è un metallo monovalente, cioè ha un solo elettrone per atomo. Si assuma una massa efficace m* = m0).
9. Si consideri la barretta di silicio drogata p (NA = 1016 cm-3) in Fig. 5. Applicando una tensione VA = 3 V, la corrente misurata IR
è pari a 200 A. Una sorgente luminosa irradia uniformemente il campione, generando un eccesso di portatori p = 5x10 cm .
Sapendo che a t = 0 s la sorgente luminosa viene spenta, e che il tempo di ricombinazione dei minoritari valga = 3 s si calcoli e
si rappresenti quantitativamente l’evoluzione temporale di IR per t ≥ 0 e VA = 1 V. (Si trascuri il contributo degli elettroni.)
14
-3
10. Si consideri una giunzione p-n, con NA<<ND = 1016 cm-3. Si stimi la minima temperatura Ti a cui le due regioni possono
considerarsi intrinseche. Si disegni il diagramma qualitativo a bande della giunzione a temperatura ambiente ed a T i. Perché la
caratteristica misurata è ohmica (I V) a Ti?
Fig. 1
Fig. 3
Fig. 2
Fig. 4
Fig. 5
Solid State Electronics
6.2.2013
1. Consider a simple cubic lattice. The interatomic distance is a = 0.34 nm. Draw the plan with index (2,1,0) and calculated the
minimum distance between two of these adjacent planes.
2. Estimate the number of confined eigenstates and the corresponding eigenvalues in the well of Fig. 1 through the infinite well
approximation. Calculate the average tunneling time for an electron in the second level E2. Calculate the electric field across the
6
barrier with width b in Fig. 1 which increases the tunneling probability by a factor 10 .
3. Consider an electron moving along the potential profile in Fig. 2 (E = 0.1 eV). Knowing that the electron velocity increases by a
factor 3 from region 1 to region 3 without scattering phenomena, calculate the initial energy E1.
4. An electron in a 1D lattice is described by the dispersion relation E(k) = E0/2*[1-cos(ka)] in Fig. 3, with E0 = 0.3 eV and a = 0.28
nm. What is the state with minimum dispersion of the wavepacket? Calculate the electric field needed to move the packet in that
state, starting from E = 0, in 1 fs. Calculate the packet velocity at that time (1 fs).
5. Calculate the increase of the number of electrons at E = 0 when temperature increases from 300 K to 400 K in the previous
exercise.
6. Fig. 4 shows the first Brillouin zone for a 2D square lattice, including the Fermi surfaces for energy levels E1 and E2. After
explaining the meaning of the Fermi surface, draw the energy E(k1) along the line k2 = 0 in the figure, qualitatively marking the
position of energy levels E1 and E2. Draw the Fermi surface directly in Fig. 4 for E3 = (E1 + E2)/2 (average between E1 and E2).
7. Consider two metallic samples with equal area, consisting of cobalt (workfunction W Co = 5 eV) and vanadium (W V = 4.3 eV),
respectively. After describing shortly the thermionic effect, estimate the vanadium temperature at which its thermionic emission
current is equal to the one in cobalt at room temperature. (Consider only the exponential term in the expression of thermionic
emission).
8. Knowing the Fermi level EF = 3.23 eV in sodium, calculate the atomic density in sodium and the electronic velocity at EF. (Note
that sodium is a monovalent metal, namely it has only one electron per atom. Assume an effective mass m* = m0).
9. Consider a p-doped silicon sample (NA = 1016 cm-3) in Fig. 5. By applying a voltage VA = 3 V, the measured current is IR = 200
A. A light source is irradiated uniformly on the sample, generating an excess carrier concentration p = 5x10 cm . Knowing that
the light source is switched-off at t = 0 s and that the minority carrier recombination time is = 3 s, calculate and draw the the time
evolution of IR for t ≥ 0 and VA = 1 V. (Neglect the electron contribution.)
14
-3
10. Consider a p-n junction with NA<<ND = 1016 cm-3. What is the minimum temperature Ti at which the two regions become
intrinsic. Draw the qualitative band diagram of the junction at room temperature and at Ti. Why is the measured characteristic ohmic
(I V) at Ti?
Costanti fisiche:
massa dell’elettrone
costante di Planck
carica elettronica
costante di Boltzmann
velocità della luce
costante dielettrica nel vuoto
costante di Stephan-Boltzmann
costante di Wien
m0 = 9.109·10 kg
-34
h = 6.626·10 J s
-19
e = 1.602·10 C
-23
-1
kB = 1.381·10 J K
8
-1
c = 2.998·10 m s
-12
-1
0 = 8.85419·10 F m
-8
-2 -4
= 5.67·10 W m K
-3
cW = 2.8·10 K m
costante dielettrica relativa r
-3
concentrazione intrinseca ni [cm ]
gap di energia EG [eV]
-3
densità di stati effettiva in banda di conduzione NC [cm ]
-3
densità di stati effettiva in banda di valenza NV [cm ]
Si
11.7
10
1.45 x 10
1.12
19
2.8 x 10
19
1.04 x 10
-31
Ge
16
13
2.4 x 10
0.66
19
1.04 x 10
19
0.6 x 10












