Pompa di calore a celle di Peltier
( 2 ) Guida all’esperienza
Scuola estiva di Genova
2 – 6 settembre 2008
Riscaldare un sistema
1
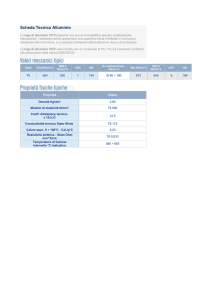
Il sistema da riscaldare è costituito da un
parallelepipedo di alluminio
Soluzione diretta
Forniamo
energia
elettrica
al
sistema
convertendola in calore mediante un resistore che
dissipa per effetto Joule.
2
Primo esperimento
• Usiamo un resistore alimentato a potenza costante
• Misuriamo la differenza di potenziale ai suoi capi
e la corrente che la attraversa :
v=v(t); i=i(t)
• Misuriamo la temperatura del parallelepipedo di
alluminio al passare del tempo :
T=T(t)
Circuito di alimentazione a potenza costante
3
Misura di tensione v e corrente di alimentazione i,
al passare del tempo t.
Misura della temperatura T,
al passare del tempo t.
4
Le quattro misure ( v, i, T, t ) devono essere prese contemporaneamente.
Suggeriamo di effettuare una misura ogni 30 secondi.
Uso delle misure
• Quanto è efficiente
riscaldamento ?
questo
metodo
di
[ Di quanti gradi aumenta la temperatura del parallelepipedo da riscaldare per ogni
joule elettrico speso ? Disegneremo la curva di riscaldamento T ( t ) ]
• Quanto è buono
parallelelepipedo ?
l’isolamento
termico
del
( Misureremo la temperatura al variare del tempo anche dopo la fine della fase di
riscaldamento. Possiamo calcolare il coefficiente di Fourier dai dati ? )
• Quanto
vale
la
capacità
parallelepipedo di alluminio ?
termica
del
5
Soluzione con celle di Peltier
Usiamo una pompa di calore a
celle di Peltier ( sfruttiamo
l’effetto di Peltier, cioè il trasporto
di calore associato a una corrente
fatta passare attraverso una
termocoppia ),
spendendo la stessa quantità di
energia elettrica del precedente
esperimento ( ne siamo sicuri
perché
usiamo
la
stessa
alimentazione a potenza costante ),
per trasferire un’ulteriore quantità di calore
dall’ambiente ( costitutito dalla base nera di alluminio
con le alette e da tutto il laboratorio ) al sistema.
6
Secondo esperimento
• Usiamo un dispositivo a celle di Peltier
alimentato a potenza costante
• Misuriamo la differenza di potenziale ai
suoi capi e la corrente che lo attraversa :
v=v(t); i=i(t)
• Misuriamo
la
temperatura
del
parallelepipedo di alluminio al passare del
tempo :
T=T(t)
Uso delle misure
• Quanto è efficiente questo metodo di riscaldamento?
[ Di quanti gradi aumenta la temperatura del parallelepipedo da riscaldare per ogni
joule elettrico speso ? Disegneremo la curva di riscaldamento T ( t ) e la
confronteremo con la precedente. ]
• Qual è il coefficiente di Fourier per la conduzione di
calore fra parallelepipedo di alluminio e ambiente ?
( Nel primo esperimento il sistema era isolato. Nel secondo esperimento c’è
conduzione di calore per effetto Fourier fra il parallelepipedo e il termostato – la
base di alluminio a contatto con l’ambiente ).
Per rispondere, dopo la fine della fase di
riscaldamento, misureremo l’andamento della
temperatura con il tempo :
T=T(t);
e anche v = v ( t ), a circuito aperto, cioè con l’amperometro sconnesso.
7