Struttura Quaternaria

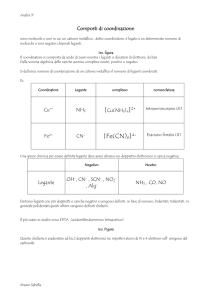
Struttura Quaternaria
Due o più subunità unite in modo non covalente
Esempi
-2 subunità identiche:
-alcool deidrogenasi
-2 o più subunità diverse:
-Hb (a2b2)
-RNA polimerasi (a2bb’s)
-piruvato deidrogenasi (t24(p2)12(f2)12)
-Strutture polimeriche a dimensioni finali variabili
-microtubuli (anbn)
1. Come si dispongono le subunità
• Simmetria: nessun legame apparente con la funzionalità
•
Il numero di subunità di un aggregato proteico è (quasi sempre –
vedi punto 3) indipendente dal ruolo funzionale
2. Quali forze stabilizzano la struttura
quaternaria
•
•
•
forze di non-legame
legami H
interazioni elettrostatiche
3. Quale ruolo assolve
Mioglobina
Emoglobina
Singola subunità Hb ~ Mioglobina
F8: His prossimale legata al Fe
Eme
E7: His distale
Fe
Prevalentemente a-elica  8 tratti A-H  connessi da tratti di random coil
MGLSDGEWQL
LEKFDKFKHL
GHHEAEIKPL
PGDFGADAQG
VLNVWGKVEA
KSEDEMKASE
AQSHATKHKI
AMNKALELFR
DIPGHGQEVL
DLKKHGATVL
PVKYLEFISE
KDMASNYKEL
IRLFKGHPET
TALGGILKKK
CIIQVLQSKH
GFQG
Solo Ca
Blow-up eme
Eme: gruppo prostetico
Fe - Protoporfirina IX
Coordinazione Fe
•
4 N della porfirina
•
1 N istidina prossimale (F8)
•
sito libero per il legame con O2
Fe  n.a. 26
Due stati di ossidazione
•
Ferroso  Fe2+  può legare O2
• Ferrico  Fe3+  non può legare O2 (meta-emoglobina  denaturazione)
Fe  n.a. 26
1s
2
2
2s
2
2
2p
6
6
3s
2
2
3p
6
6
3d
6
5
Shell incomplete
Fe2+
Fe3+
Il concetto di cooperatività
L'affinità per il legante (O2 nell'emoglobina) modificata da un
cambiamento conformazionale

modulato dal legame di una (o più di una) subunità con il legante
Hb  scatto conformazionale (della struttura quaternaria) quando da due a
tre delle quattro subunità legano legante

aumento (~ 300 volte) dell'affinità delle subunità non ancora legate
curva di saturazione con l’ O2
Confronto tra Hb (a più subunità) e Mb (singola subunità)
Y: saturazione frazionaria = rapporto tra concentrazione di proteina (o
subunità, nel caso dell’Hb) legata con O2 e concentrazione totale.
pO2: pressione parziale di ossigeno
Mb + O2
Y
MbO2 
MbO2   Mb
k
Mb  1
1
1 
MbO2  kpO2
Y
MbO2
MbO2 
MbO2 

MbO2 
kpO2 
Mb
kpO2
Y
1  kpO2
Iperbole equilatera
Y
k  pO2 n
1  k  pO2 n
Forma generale  n = 1 non cooperativo (singola subunità)
n > 1 cooperatività
X
Hb: la pendenza della curva
di saturazione cambia al
variare di pO2
Y
k  pO2 n
1  k  pO2 n
Il modello di Monod-Wymann-Changeux (MWC)
Ipotesi:
1. promoteri identici occupano posizioni strutturalmente equivalenti nella
proteina, che equivale a dire che la proteina ha almeno un asse di simmetria
2. ciascun promotero ha almeno un sito per ciascuno dei diversi ligandi
(definizione di promotero);
3. Esistono almeno due stati conformazionali (strutture) reversibilmente
accessibili alla proteina per i quali deve valere:
i. in ciascuno degli stati la simmetria di cui al punto 1 è conservata;
ii. l’affinità per una dato legante può essere anche molto diversa nei due
stati
4.
l’affinità per uno specifico legante dipende dallo stato conformazionale
dell’intero enzima.
Nota: Interazione omotropica: l’affinità per un legante è influenzata da quanto legante
dello stesso tipo è già legato ( cooperatività).
Interazione etrotropica: il legame di un legante (al suo specifico sito di legame) ha
effetto sull’affinità di legame di un altro (es: effetto Bohr , affinità e pH)
Il caso dell’Hb.
# promoteri=n=4
2 stati: R (relaxed) e T (tense)
.
Per rispettare la condizione (3i) solo alcune combinazioni di
stati dei singoli promoteri sono permesse.
… e analoghe per lo stato tense
Dove kR
(kT) è la costante di dissociazione microscopica (reazione di
dissociazione del singolo legante dal singolo sito di legame) nello stato
relaxed (tense)
Nota: la costante di dissociazione microscopica è sempre la stessa indipendentemente
dallo stato di occupazione degli altri siti  i 4 siti sono implicitamente ipotizzati
essere indipendenti.
Si possono quindi scrivere le seguenti reazioni di equilibrio
R0 + L
R1 + L
R2 + L
R3 + L
R1
R2
R3
R4
T0 + L
T1 + L
T2 + L
T3 + L
T1
T2
T3
T4
Ri (Ti ): specie microscopica con i leganti L legati nello stato R (T )
K1 
M 0 L
M 1 
K2 
M 1 L
M 2 

Kn 
M n1 L
M n 
Per una generica molecola, M, con n siti.
Per il generico i-esimo sito
e
M i 1

M i 2 L

K i 1

M i 1 L
Ki 
M i 
ovvero
che sostituita nella precedente
M i   M i1 L
Ki
M i   M i2 LL
K i K i 1
i
M i   M 0 L  K j
e infine
i
j 1
Ci sono
 n,i
n!

i!(n  i)!
modi distinti di disporre i leganti in n siti
da cui la seguente generica relazione tra costanti macroscopiche e microscopiche
Ki 
 n,i 1
 n,i
n!
i!(n  i)!
i!(n  i)!
k
k
k
(i  1)!(n  1  i)! n!
(i  1)!(n  1  i)!
L’esempio dell’Hb
R e T siano i due stati conformazionali
kR  kT (ipotesi 3.ii) 
kR
kT 
C
con C = costante >1
 la costante di dissociazione microscopica è maggiore nello stato T ( il
legante preferisce stare legato alla forma R)
Dalla precedente relazione tra costanti macroscopiche e microscopiche
K1 
 n,i 1
 n,i
kR
i!(n  i)!
1!(4  1)!
kR 
kR 
kR 
(i  1)!(n  1  i)!
0!(4  1  1)!
4
ed equivalentemente
2k R
3k R
K2 
; K3 
;
3
2
K 4  4k R
Dalle reazioni di equilibrio
[ R0 ][ L] k R

[ R1 ]
4
[ R ][ L] 2k R
K2  1

[ R2 ]
3
[ R ][ L] 3k R
K3  2

[ R3 ]
2
[ R ][ L]
K4  3
 4k R
[ R4 ]
K1 
E analoghe per lo stato T
Che utilizzando le definizioni
a
[T ]
[ L]
; Q 0
kR
[R 0 ]
diventano
[ R1 ]  4[ R0 ]a
[ R2 ]  6[ R0 ]a 2
dove [T0 ] e[R 0 ] sono le concentrazioni delle
[ R3 ]  4[ R0 ]a 3
subunità prive di leganti rispettivamente in T e R
[ R4 ]  [ R0 ]a 4
Utilizzando la
Q
[ L]
4  4Q[ R0 ]Ca
kT
[T2 ]  6Q[ R0 ]C 2a 2
[T3 ]  4Q[ R0 ]C 3a 3
[T4 ]  Q[ R0 ]C 4a 4
[T1 ]  Q[ R0 ]
[T0 ]
[R 0 ]
si ottengono le relazioni equivalenti per T
La saturazione frazionaria sia data da
i[ Ri ]  i i[Ti ]

i
YL 
4i [ Ri ]  i [Ti ]
Dove, al numeratore sono sommate le concentrazione totali di siti occupati con
un numero qualsiasi, i, di leganti in uno dei due stati conformazionali e al
numeratore la concentrazione totale.
Riscrivendo le varie sommatorie in funzione di a, C, [R0] e Q
i 4
 [ R ]  [ R ](1  4a  6a
i 0
i
0
2
 4a 3  a 4 ) [ R0 ](1  a ) 4
i 4
4
[
T
]

Q
[
R
]
(
1

C
a
)
 i
0
i 0
i 4
2
3
4
3
i
[
R
]

0

[
R
]

1

4

[
R
]
a

2

6

[
R
]
a

3

4

[
R
]
a

4

[
R
]
a
)

4
[
R
]
a
(
1

a
)
 i
0
0
0
0
0
0
i 0
i4
3
i
[
T
]

4
Q
[
R
]
C
a
(
1

C
a
)
 i
0
i 0
La saturazione frazionaria si può
scrivere per n=4
Se
a (1  a ) 3  QCa (1  Ca ) 3
YL 
(1  a ) 4  Q(1  Ca ) 4
[T0 ]  0 (subunità indipendenti o singola subunità), anche Q  0 , quindi
a (1  a ) 3
a
YL 

1a
(1  a ) 4
E per n qualsiasi
la curva di saturazione è un iperbole.
a (1  a ) n1  QCa (1  Ca ) n1
YL 
(1  a ) n  Q(1  Ca ) n
Andamento di YL in funzione della concentrazione di legante
• bassa concentrazione di legante libero
a
[ L]
 1
kR
a (1  a )3
a
YL 

(1  a ) 4  Q Q
YL
Retta di pendenza
[R ]
Q 1  0
[T0 ]
a
• dove
YL 
1  a  Q  1 
a (1  a ) 3
Q
[T ]
[ L]
 0
kR
[ R0 ]
a
3a 2 3a 3 a 4
 


Q
Q
Q
Q
YL varia rapidamente per piccole variazioni di a 
[ L]
e quindi di [L]
kR
YL
a
• dove
[ L] [T0 ]
a Q

 1
k R [ R0 ]
[L] è grande  tutti i siti sono saturati con il legante
YL
YL  1
Si noti che la sigmoicità
a
[T0 ]
• cresce al crescere di Q 
[ R0 ]
• decresce mentre
C
kR
1
kT
Le frecce in verde indicano il modello descritto da Perutz per l’Hb
M.F.Perutz “Mechanism of cooperativity and allosteric regulation in
proteins”, (1989) Quart.Rev.Biophys., 22, 139-236.
Effetto Bohr