Capitolo 3
Sistemi sequenziali
3.1
Sincronizzazione dei sistemi sequenziali
Consideriamo un flip-flop dinamico di tipo D, a singola fase, sincronizzato sul fronte di discesa del
clock (Fig. 3.1).
Fig. 3.1 - Flip-flop dinamico di tipo D a singola fase
Fig. 3.2 - Temporizzazione del flip-flop
Capitolo 3
164
Vediamo quali sono le relazioni temporali da rispettare per avere un corretto funzionamento del
flip-flop. Considerando il diagramma temporale di figura 3.2, il segnale D dovrà stabilizzarsi prima
del fronte attivo del clock (cioè quello di discesa). L’intervallo di tempo minimo che intercorre fra
l’ultima variazione di D e il fronte attivo del clock prende il nome di tempo di setup, ts. Inoltre è
necessario che D resti stabile anche per un tempo successivo al fronte del clock. Si definisce allora
tempo di hold, th, il minimo intervallo di tempo che deve trascorrere dal fronte attivo del clock
prima che si verifichi una variazione di D. Se D varia nell’intervallo ts+th non è più garantito il
corretto funzionamento del flip-flop, il quale può entrare in uno stato metastabile (o comunque
avere un funzionamento per cui le uscite diventano impredicibili).
L’uscita Q, a causa delle non idealità dei dispositivi impiegali, varierà con un certo ritardo rispetto
al fronte attivo del clock. Si definisce allora il tempo tq, detto clock-to-q delay, come l’intervallo di
tempo minimo, che deve trascorrere dal fronte attivo del clock per avere un’uscita Q stabile.
Il ritardo ts è legato al tempo necessario perché la capacità CM si carichi (o si scarichi).
Analogamente il tempo tq è legato alla carica o scarica della capacità CS; infatti, l’uscita varia
quando la fase φ si abbassa, cioè quando lo slave diventa trasparente. Da questo istante di tempo
bisogna dar modo alla capacità Cs di caricarsi o scaricarsi; ci sarà quindi un ritardo
(sostanzialmente dovuto all’invertitore) responsabile del tempo tq.
Per quanto riguarda il tempo di hold, possiamo pensare che i segnali φ e φ siano generati nel modo
mostrato in figura 3.3.
Fig. 3.3 - Generazione dei segnali φ e φ
Cioè, partendo da un segnale di clock esterno, con un primo invertitore si ricava il segnale φ e
mentre un secondo invertitore fornisce il segnale φ.. Quindi cambiamo lo stato del nostro flip-flop
non nell’istante di tempo in cui cambia il segnale di clock (ck) accessibile dall’esterno ma un po’
dopo, dato che bisogna dare il tempo al segnale ck di essere invertito e poi attivare le porte di
trasmissione. Quindi, il dato che bisogna catturare nel registro deve essere presente anche per un
certo intervallo di tempo dopo che il segnale di clock è variato.
Notiamo che in questa analisi stiamo facendo una serie di approssimazioni; infatti, ad esempio, il
ritardo clock-to-q può essere diverso a seconda che l’uscita Q debba portarsi da O ad i o viceversa
(quindi, bisognerebbe considerare tq, 0Æ1 e tq, 1Æ0). Discorso analogo vale per il tempo di setup e
quello di hold. Per semplicità di analisi, quindi, ci limitiamo a considerare i tre tempi: ts, th e tq.
Una volta definiti questi tre valori vediamo come vengono utilizzati per determinare le condizioni di
buon funzionamento di un sistema sequenziale qualsiasi. In particolare facciamo riferimento a dei
sistemi sequenziali sincroni, disinteressandoci totalmente di quelli asincroni, per una serie di motivi;
Sistemi sequenziali
165
innanzitutto i sistemi sincroni sono quelli più semplici e più affidabili, inoltre sono quelli per i quali
è possibile effettuare delle operazioni di testing dopo che il sistema è stato realizzato (i sistemi
asincroni, invece, sono praticamente impossibili da testare una volta realizzati).
Per questi motivi, quindi, nelle applicazioni vengono esclusivamente utilizzati dei sistemi sincroni,
a meno di casi particolari in cui sia necessario realizzare sistemi sequenziali asmcroni.
Nei sistemi sincroni, quindi, tutto avviene in corrispondenza dei fronti attivi di un segnale di clock
(cioè non sono le variazioni degli ingressi che innescano le transizioni del sistema).
In generale, un sistema sequenziale (macchina a stati) può essere rappresentato come in figura 3.4,
ovvero un sistema combinatorio connesso con un insieme di elementi di memoria (n flip-flop di tipo
D). Tutti i registri sono triggerati da un unico segnale di clock, il quale con i suoi fronti attivi
cadenza il funzionamento del sistema sincrono.
Lo stato attuale, x, del sistema entra in ingresso al sistema combinatorio, viene calcolato lo stato
futuro y, che viene riportato in ingresso al banco di registri. Vi possono poi essere degli ulteriori
ingressi e uscite del nostro sistema sequenziale. Per ottenere le condizioni per un corretto
funzionamento del nostro sistema disinteressiamoci, per il momento, di questi ingressi ulteriori,
ovvero ipotizziamo che anche questi ingressi provengano (così come lo stato attuale) dall’uscita di
un banco di registri pilotato dallo stesso segnale di clock. Infatti se questi ingressi variano in
maniera scorrelata con il segnale di clock, come vedremo, si potrebbero avere degli errori di
sincronizzazione.
Fig. 3.4 - Sistema sequenziale sincrono
Supponiamo che i registri siano sincronizzati sul fronte di discesa del clock e consideriamo il
diagramma temporale di figura 3.5. L’uscita x, stato attuale del nostro sistema combinatorio, in
generale sarà formata da n bit (n variabili di stato) e potrà cambiare soltanto dopo il fronte attivo del
clock, con un ritardo pari a tq. L’uscita y del sistema combinatorio non potrà che variare dopo che è
Capitolo 3
166
variato l’ingresso x. Poiché abbiamo n uscite di questo sistema combinatorio, è probabile che alcune
di queste varino più velocemente di altre. Di queste, quindi, alcune si assesteranno subito dopo la
variazione dell’ingresso, altre con un ritardo maggiore. Possiamo dunque definire due parametri: un
ritardo combinatoriale minimo (tc,min) e un ritardo combinatoriale massimo (tc,max), indicati in Fig.
3.5. Inoltre T è il periodo del clock.
Fig. 3.5 - Diagramma temporale del sistema sequenziale sincrono
Il ritardo combinatonale massimo dipenderà dal cammino critico presente nel nostro sistema
combinatoriale; inoltre il ritardo minimo, ad esempio, può valere 0 perché l’uscita di un registro è
collegata direttamente con l’ingresso di un altro flip-flop. Tale sistema prende il nome di registro a
scorrimento, caso particolare di macchina a stati in cui il sistema combinatorio che collega l’uscita
di un flip-flop con l’ingresso di un altro ha un ritardo combinatoriale minimo (e massimo) sempre
pari a zero (a parte il ritardo introdotto dalle interconnessioni).
Il sistema funzionerà correttamente se sono rispettati i vincoli relativi al tempo di setup e al tempo
di hold. Si riuscirà a catturare il valore corretto dello stato futuro del sistema se l’uscita y diventa
stabile sufficientemente prima rispetto al successivo fronte del clock, con un margine che abbiamo
chiamato tempo di setup (ts). Quindi la condizione che deve essere rispettata per avere un corretto
funzionamento del sistema è la seguente:
T > tq + tc,max + ts
Questa condizione, da verificate affinché il vincolo sul tempo di setup sia soddisfatto, ci dice che la
frequenza massima del clock è limitata dal ritardo massimo del nostro sistema combinatorio. Oltre a
Sistemi sequenziali
167
questo, però, entrano in gioco anche due parametri tipici dei registri utilizzati: tq e ts; quindi, un
parametro che definisce la velocità dei nostri registri non è soltanto tq, ma la somma tq + ts (non è
importante soltanto il ritardo da quando varia il fronte del clock a quando varia l’uscita dei registri,
ma è anche importante che ts sia piccolo).
Bisogna però rispettare anche il vincolo sul tempo di hold. Osserviamo che in seguito al fronte
attivo del clock vi sarà una variazione di x, e quindi una variazione di y; ma y è ancora un ingresso
per il registro. Quindi l’inizio della variazione di y, dopo il fronte attivo del clock, deve avvenire
sufficientemente dopo rispetto al tempo di hold del flip-flop, altrimenti gli ingressi (y) del flip-flop
varierebbero proprio in prossimità del fronte attivo del clock. Quindi deve risultare:
tq + tc,min > th
Questa seconda condizione (meno scontata della precedente) ci dice che gli ingressi dei nostri flipflop non possono variare proprio in prossimità dei fronte attivo dei clock, ma devono variare dopo
un certo intervallo di tempo (pari a th). Notiamo che in questa disequazione non compare né il
periodo del clock (T) né il ritardo combinatoriale massimo.
Ciò vuoi dire che possiamo sempre pensare di rispettare il primo vincolo (quello su ts) abbassando
la frequenza del clock. Nonostante ciò, se non è verificata la condizione sul tempo di hoid, anche se
si abbassa la frequenza del clock il circuito continua a non funzionare. Quindi questa seconda
condizione non è tanto legata alle prestazioni del nostro circuito ma proprio alla condizione di
corretto funzionamento del circuito.
Osserviamo, inoltre, che questa seconda condizione è tanto più difficile da rispettare quanto più è
piccolo il ritardo combinatoriale minimo; cioè quanto più è veloce il sistema combinatoriale tanto
più è difficile rispettare questa disuguaglianza. Da ciò si deduce che in molti casi, per valutare il
corretto funzionamento di un circuito, non bisogna considerare come caso peggiore quello in cui il
circuito è più lento di quanto ci potevamo aspettare; m alcune circostanze il caso peggiore è
l’angolo di processo in cui tutti i circuiti sono un po’ più veloci rispetto alle condizioni nominali di
funzionamento.
Da quanto detto si deduce che la condizione peggiore possibile è quella in cui tc,min =0 (condizione
non ipotetica, ma corrispondente al caso in cui l’uscita di un flip-flop è collegata direttamente ad un
flip-flop successivo); in tal caso il nostro circuito funziona correttamente soltanto se: tq > th,
condizione valevole per il singolo flip-flop. Quindi il circuito funziona correttamente se i singoli
flip-flop sono progettati in modo tale che tq + tc,min > th.
In definitiva, il primo vincolo (quello su ts) può essere rispettato abbassando la frequenza di clock,
ovvero rallentando il nostro sistema combinatorio; quindi questo vincolo determina le prestazioni
del nostro sistema, ovvero la frequenza massima di funzionamento. Il secondo vincolo (quello su th)
non dipende né dalla frequenza del clock né tanto meno dal ritardo massimo del sistema
combinatorio, viceversa dipende dal ritardo minimo del sistema combinatorio; poiché quest’ultimo
può anche essere uguale a zero, per avere un corretto funzionamento del nostro sistema in pratica
bisogna garantire che per ogni flip-flop sia tq>th.
Capitolo 3
168
In generale questa condizione è, in pratica, sempre verificata dato che th è legato al ritardo fra fronte
attivo del clock e l’istante in cui le porte di trasmissione si aprono o si chiudono. Il tempo tq, invece,
porta in conto, oltre al ritardo fra l’istante in cui varia il clock e l’istante in cui le porte di
trasmissione si aprono o si chiudono, anche il ritardo dovuto al latch che funziona come slave. Ciò
fa si che per il singolo flip-flop risulti sempre tq>th (a meno di casi eccezionali).
Nonostante ciò, anche se per il singolo flip-flop risulta tq>th, possiamo avere una violazione del
vincolo sul tempo di hold. Tale possibilità nasce dal fatto che non siamo sicuri che il segnale di
clock arrivi istantaneamente a tutti i flip-flop, ma ci sarà un ritardo introdotto dalla linea di clock.
Questo ritardo fa si che non tutti i flip-flop commutino nello stesso istante; anche se questo ritardo
può essere molto breve, tuttavia può pregiudicare il funzionamento del nostro sistema.
3.2
Ritardo sul clock (clock-skew)
Quindi bisogna estendere le due relazioni precedenti per portare in conto il ritardo sulla linea di
clock. Consideriamo il sistema sequenziale di figura 3.6, in cui sulla linea di clock supponiamo sia
presente un elemento di ritardo ∆.
Fig. 3.6 - Sistema sequenziale con ritardo sulla linea di clock
Pertanto al secondo registro arriverà un segnale di clock, ck’, ritardato di ∆ rispetto al segnale ck
che giunge al primo. Consideriamo allora il diagramma temporale di figura 3.7 per valutare in quali
condizioni sono verificati i vincoli sul tempo di setup e sul tempo di hold.
Con un ritardo pari a tq rispetto al fronte attivo del clock varierà l’uscita del primo banco di registri.
Alcuni dei bit dell’uscita w del sistema combinatorio cominceranno a variare con un ritardo tc,min
dalla transizione di y, per altri sarà necessario un tempo tc,max per assestarsi. Per il secondo banco di
registri il segnale di clock non è ck, ma ck’, ritardato di ∆ rispetto a ck.
Per quanto riguarda il vincolo sul tempo di setup, il fatto che ci sia questo ritardo ∆ è un fatto
positivo, dato che si ha più tempo perché il sistema combinatorio possa completare la sua
elaborazione; ciò fa si che questo vincolo sia rispettabile più facilmente.
Sistemi sequenziali
169
Fig 3.7 - Diagramma temporale del sistema sequenziale con ritardo sul clock
La condizione che deve essere verificata, in questo caso, sarà allora:
T + ∆ > tq + tc,max + ts ⇒ T > tq + tc,max + ts - ∆
Quindi, grazie a questo ritardo D è possibile migliorare le prestazioni del nostro sistema, dato che è
possibile aumentare la frequenza di clock Osserviamo, però, che ∆ è il ritardo introdotto da una
linea d’interconnessione, quindi il suo valore è estremamente ridotto; sicuramente sarà molto più
piccolo di tc,max . Inoltre, non si può nemmeno pensare di introdurre deliberatamente un ritardo
sulla linea di clock dato che bisogna tener conto del vincolo sul tempo di hold.
Infatti, il fatto che ck’ sia ritardato di A rispetto a ck rende più difficile il rispetto del vincolo su th,
dato che ora questo vincolo coinvolge il fronte attivo di ck’ e la prima variazione del segnale w. In
definitiva la condizione che deve verificarsi è la seguente:
tq + tc,min - ∆ > th ⇒ ∆ < tq + tc,min - th
Osserviamo, quindi, che quando si ha un ritardo sulla linea di clock è come se il ritardo del flipflop, tq, diventi tq - ∆. Da questo vincolo, pertanto, si deduce che il ritardo sul clock risulta essere
alquanto problematico, dato che nel caso peggiore in cui tc,min=0 se ∆ diventa maggiore di tq risulta
Capitolo 3
170
impossibile verificare il vincolo sul tempo di hold. Quindi, per garantire un corretto funzionamento
del nostro sistema, ovvero una corretta sincronizzazione del nostro sistema, il ritardo sulla linea di
clock deve essere sufficientemente piccolo (in base alla condizione precedente). Se tc,min=0, ∆ deve
essere minore della differenza fra tq e th, differenza che risulta essere estremamente piccola
(sicuramente al di sotto del ns).
Questo problema del ritardo sul clock prende il nome di clock-skew, che rappresenta uno dei
problemi più complicati da risolvere quando si cerca di migliorare sempre di più le prestazioni dei
sistemi digitali. Infatti, grazie soprattutto ai progrèssi tecnologici, si riescono a ridurre sempre di più
i tempi di propagazione, ovvero tq e th diventano sempre più piccoli. Se pensiamo allora che
attualmente esistono microprocessori che funzionano ad un frequenza di clock dei GHz, per i quali
quindi possiamo ipotizzare che tq sia dell’ordine di qualche decina di ps (sicuramente al di sotto del
centinaio di ps), è chiaro che il ∆ massimo che può essere tollerato è dell’ordine di grandezza di
qualche di ps, all’interno di un circuito che può essere molto complicato (può avere centinaia di
milioni di transistors).
Quindi non è possibile affatto aumentare ∆ per aumentare la frequenza di funzionamento del nostro
sistema, dato che si viola il vincolo sul tempo di hold.
Osserviamo però che se riuscissimo a realizzare un ∆ negativo potremmo rispettare molto più
facilmente il vincolo sul tempo di hold e avremmo un po’ peggiorato le prestazioni del nostro
sistema anche se in maniera irrilevante, dato che ∆ è sempre molto più piccolo di tc,max. Per
realizzare un ∆ negativo basta inviare il clock in senso opposto al flusso dei dati; ciò in alcuni casi è
possibile, ma non sempre. In particolare, se siamo noi a posizionare manualmente i vari blocchi
possiamo avere un controllo sulla direzione del flusso dei dati e del flusso del clock; ma se questi
vengono posizionati, ad esempio, in maniera automatica risulta ben difficile realizzare questa
situazioni. Inoltre, possono esserci delle condizioni in cui non c’è un’unica direzione in cui
fluiscono i dati. Ad esempio, nel sistema mostrato in figura 3.8 riscontriamo che i dati fluiscono in
direzioni opposte; pertanto comunque colleghiamo il clock, in una direzione avremo un ∆ negativo
e nell’altra un ∆ positivo.
Fig. 3.8 - Esempio di sistema con flusso dei dati in direzioni opposte
Sistemi sequenziali
171
Nei casi in cui si sa a priori come sono piazzati i sistemi combinatori e i registri, e sappiamo che il
flusso dei dati ha sempre una stessa direzione, allora possiamo pensare di distribuire il clock in
direzione opposta. Viceversa per garantire che il vincolo sul tempo di hold sia rispettato bisogna
ridurre al massimo il valore di ∆. Osserviamo che il fattore che può dar luogo ad un problema di
sincronizzazione non è il ritardo fra il punto in cui viene applicato il segnale di clock e i vari
registri, ma è importante che il clock arrivi contemporaneamente ai vari registri.
Un possibile esempio, molto semplice, di distribuzione del clock è costituito dalla cosiddetta
struttura ad H, mostrato in figura 3.9.
Fig. 3.9 - Distribuzione del clock: struttura ad H
Supponiamo che il nostro sistema sia costituito da un certo numero di blocchi (celle standard,
registri, ecc.), cui deve arrivare il segnale di clock, e supponiamo siano disposti in maniera
periodica. Si distribuirà il segnale di clock in modo tale che ci sia una distribuzione simmetrica per
tutti i blocchi. In pratica si disegnano delle “H” che collegano fra loro i blocchi, evidenziandone il
punto centrale. Da questo punto di centro ad ognuno dei vari blocchi il ritardo del clock sarà lo
stesso. Procedendo in maniera analoga per tutto il circuito si ottiene la distribuzione (ad albero) ad
H del clock. Osserviamo che l’istante in cui si applica il clock nel punto centrale della struttura non
è lo stesso in cui il clock arriva ad uno dei blocchi; ciò però non è importante, ciò che conta è che il
clock arrivi all’incirca nello stesso istante a tutti i vari blocchi del nostro sistema. Ovviamente le
cose non sono così banali dato che non tutti i blocchi saranno uguali, non hanno tutti lo stesso
carico (cioè le strutture non sono cosi regolari); in linea di principio, comunque, una tecnica che si
può adoperare è quella di bilanciare i ritardi sulla linea di clock, per fare in modo che questo
segnale arrivi possibilmente in maniera simultanea a tutti gli elementi di memoria.
Un’altra tecnica per contrastare il ritardo ∆ sul clock è quella di aumentare il tq. Ciò può essere fatto
o soltanto per quei registri che sono collegati in qualche modo a dei sistemi combinatori che
172
Capitolo 3
presentano un ritardo molto basso (ma ciò ci costringe a identificare per quali registri bisogna
aumentare il tq e per quali no), oppure possiamo pensare di aumentare il tq per tutti i registn. Questa
seconda strategia, però, se da un lato ci assicurerà il soddisfacimento del vincolo sul tempo di hold,
dall’altro comporterà un peggioramento delle prestazioni.
Un modo per aumentare il tq su tutti i registri è quello di utilizzare un clock a due fasi (che fra
l’altro permette di evitare anche i problemi legati alle sovrapposizioni fra φ e φ), dove le due fasi
devono essere non overlapping (Fig. 3.10). In questo caso consideriamo come clock il segnale di
fase φ1; per avere un corretto funzionamento del nostro sistema bisogna garantire un margine ts e un
margine th rispetto al fronte di discesa del clock. Per quanto riguarda l’uscita Q essa comincerà a
variare dopo che φ2 si è alzato, con un ritardo tq,i, che possiamo considerare intrinseco del nostro
flip-flop. Se guardiamo il flip-flop dall’esterno esso è comandato dal clock ck (≅φ1), ignorando che
ci sia una fase φ2 anch’essa distribuita, e presenta un tempo di ritardo tq = tq,i + tnov.
Fig. 3.10 - Utilizzo di un clock a due fasi per risolvere il problema del clock-skew
Quindi è possibile aumentare tq aumentando il tempo di non overlap; in particolare, si sceglie questo
tempo in modo che tnov ≅ ∆ in modo tale da compensare il ritardo massimo che è possibile avere
sulla linea di clock. Quindi, rispetto ad un registro a singola fase, con un registro a due fasi è
possibile agire su due parametri: la frequenza di clock, che possiamo aumentare per cercare di
soddisfare il vincolo su ts, ed il tempo di non overlap, che possiamo pensare di aumentare per
cercare di soddisfare anche il vincolo su th. Tutto ciò, ovviamente, va a discapito delle prestazioni in
quanto si rallentano tutti i flip-flop (dato che aumenta tq.). Per questo motivo tale tecnica è ormai
poco utilizzata.
Sistemi sequenziali
173
Vediamo allora cosa succede se realizziamo il sistema combinatorio in modo tale che il tc,min sia
comparabile con il tc,max. Osserviamo, innanzitutto, che ciò è molto difficile da realizzare in quanto
bisogna progettare il nostro sistema combinatorio in modo tale che tutti i ritardi soddisfino due
vincoli (devono essere minori di una certa grandezza e maggiori di un’altra). Si sceglie allora il ∆ in
modo da verificare al limite il vincolo sul tempo di hold, ovvero scegliamo:
∆lim = tq - th + tc,min
Andando a sostituire nella relazione che esprime il vincolo sul tempo di setup si ottiene:
Tmin = tq + ts + tc,max – (tq - th + tc,min) = ts + th + ( tc,max - tc,min)
Questa relazione ci dice che se riusciamo a rendere il tc,min comparabile con il tc,max e siamo in
grado di controllare il ∆, possiamo operare ad una frequenza di clock legata non a tc,max, ma alla
differenza (tc,max - tc,min), quindi molto più elevata. Questa tecnica di progetto, molto rischiosa perché
si basa sull’ipotesi di riuscire a controllare perfettamente il ritardo sulla linea di clock (rendendolo
pari a ∆lim) e di riuscire a progettare un sistema combinatorio con un tc,min prossimo a tc,max prende il
nome di wave-pipelining. Questo nome deriva dal funzionamento “ad onda” del nostro sistema, in
quanto mentre si propaga il segnale rallentiamo anche il clock, in modo che queste due onde
procedano nel nostro circuito in modo tale che il fronte del clock riesce comunque di volta in volta a
catturare il dato giusto per ogni flip-flop. Questa tecnica è un settore in sviluppo, non è una tecnica
standard di progetto; ad esempio, le strutture CPL che sono caratterizzate dal fatto di essere
costituite sempre dalla stessa cella (un multiplexer, indipendentemente dalla funzione che si sta
realizzando) ben si prestano, sotto certe particolari condizioni, a realizzare dei sistemi in cui il
tempo combinatoriale minimo e massimo siano non molto diversi fra loro.
Osserviamo che finora abbiamo considerato dei flip-flop come elementi di memoria. In generale,
non è possibile utilizzare dei latch come elementi di memoria; infatti consideriamo la nostra
macchina a stati (Fig. 3.11) in cui però come registro utilizziamo un insieme di latch.
Fig. 3.11 - Macchina a stati con registro a latch
Capitolo 3
174
Considerando il diagramma temporale di figura 3.12, supponiamo che i latch siano trasparenti
quando il segnale di clock è alto. Dall’istante in cui il clock diventa alto l’uscita x comincia a
variare, con un certo ritardo tq.
Fig. 3.12 - Diagramma temporale del sistema sequenziale con registro a latch
Alcune delle uscite y . a valle del sistema combinatorio cominceranno a variare dopo il segnale x,
con un ritardo tc,min, altre con un ritardo maggiore (tc,max) prima di assestarsi. Si deduce, allora, che
per avere un corretto funzionamento del nostro sistema deve verificarsi la condizione:
tq + tc,min > tON + th
Se, infatti, il tempo tq + tc,min fosse minore di tON si ha che alcune uscite comincerebbero a variare
quando il latch è ancora trasparente, le quali quindi si presenterebbero in ingresso al sistema
combinatorio mentre altre sono ancora in elaborazione. Pertanto, quando il clock si abbassa, per
alcune uscite verrebbe memorizzato il valore giusto mentre per altre un valore sbagliato,
corrispondente addirittura al clock successivo.
Inoltre deve essere rispettato sempre l’altro vincolo sul tempo di setup, ovvero:
tq + tc,max + ts < T
Quindi abbiamo due vincoli sul clock: uno sul periodo T del clock (che deve essere maggiore di una
certa quantità) e l’altro sul periodo tON in cui il clock è alto (che deve essere minore di un’altra
quantità). Questo doppio vincolo sul clock è difficile da rispettare; inoltre, se tc,min =0, il tON deve
essere dell’ordine di pochi decimi di ns.
Per queste difficoltà, in pratica, questa tecnica non può essere utilizzata (a meno che tON non diventi
un impulso di durata infinitesimale, il che non è facile da realizzare). Pertanto invece dei latch
bisogna fare riferimento sempre a dei flip-flop.
Sistemi sequenziali
175
Vediamo adesso come è possibile realizzare un flip-flop che abbia un segnale di abilitazione
(enable), che vada ad aggiornare il suo stato se è attivo il segnale di enable, mentre mantenga lo
stato precedente se il segnale di enable è zero. Una semplice realizzazione che possiamo pensare di
realizzare è quella di figura 3.13, cioè mettiamo il clock in AND col segnale di enable.
Fig. 3.13 - Realizzazione del clock-gating
Se en=l i segnali ck e ck’ sono uguali fra loro, mentre se en=0 ck’=0 ed il circuito non carica il
nuovo valore di D. In questo tipo di approccio ci sono almeno due problemi. Il primo problema, di
tipo elettrico, consiste nel fatto che, se il registro è un registro dinamico, sappiamo che questo
funziona correttamente se la frequenza di clock è maggiore di un certo valore limite.
Con un circuito di questo tipo può verificarsi che il segnale di enable sia pari a zero per un tempo
molto lungo; in questo caso ck’ resta pari a zero ed il flip-flop non ha un refresh (le capacità
perdono il loro effettivo stato di carica). Il funzionamento del circuito, pertanto, è pregiudicato dato
che lo stato di questo flip-flop dopo un po’ di tempo diventa indefinito. A parte questo problema
legato all’utilizzo di un flip-flop dinamico, osserviamo che l’altro problema è dovuto al fatto che
sulla linea di clock è stato introdotto deliberatamente un ritardo ∆, quello della porta AND. Infatti,
se l’ingresso D proviene da un altro registro, il cui clock è ck, c’è la quasi certezza che il circuito
non funzioni, dato che per il primo registro il ritardo combinatoriale minimo è praticamente zero,
mentre per il secondo c’è un ritardo sul clock dovuto alla porta AND.
Quindi, questa tecnica, che prende il nome di clock-gating, non può essere applicata dato che induce
problemi di sincronizzazione. In generale, quando si ha un circuito in cui non arriva sempre lo
stesso identico segnale a tutti i morsetti di clock, bisogna fare molta attenzione perché potrebbe non
funzionare o, comunque, funziona solo se sono verificati certi vincoli. Il corretto funzionamento di
un sistema sincrono prevede che lo stesso segnale di clock, possibilmente distribuito in maniera tale
che i ritardi siano uguali, arrivi a tutti i flip-flop.
Capitolo 3
176
L’abilitazione può allora essere realizzata come mostrato in figura 3.14, premettendo all’ingresso
del flip-flop un multiplexer comandato dal segnale di enable (en). Se en=l il dato d’ingresso (Din)
prosegue verso il nostro flip-flop, mentre se en=0 si riporta l’uscita Q in ingresso; in questo modo
non si introduce alcun ritardo sul clock.
Fig. 3.14 - Flip-flop con segnale di enable
3.3
Sistemi a “vera” singola fase di clock (TSPC)
Uno dei problemi che si presenta per i flip-flop è quello legato alla sovrapposizione fra i segnali φ e
φ ; tale problema è particolarmente evidente per i registri di tipo dinamico. Se infatti consideriamo il
flip-flop di figura 3.1, se φ e φ sono entrambi 1 (o entrambi 0) il circuito non funziona
correttamente; ad esempio, se sono entrambi 1 i due NMOS delle porte di trasmissione sono in
conduzione ed il circuito è trasparente (ovvero ogni variazione sull’ingresso D la si ritrova
sull’uscita Q, a parte un certo ritardo).
Una prima struttura, molto semplice, che permette di risolvere almeno in parte questo problema si
basa sulla realizzazione di un flip-flop dinamico utilizzando dei clocked-inverter (Fig. 3.15). A
livello transistor questo circuito si presenta come mostrato in figura 3.16; notiamo che
l’occupazione di area è pressappoco quella di due invertitori.
Fig. 3.15 - Flip-flop dinamico a clocked-inverter
Oltre al vantaggio in termini di occupazione di area, questa struttura risulta essere insensibile
all’overlap fra ck e ck. Infatti se supponiamo di trovarci nella condizione in cui, in un certo
intervallo di tempo, sia ck che ck sono entrambi pari ad 1, saranno in conduzione sia l’NMOS
pilotato da ck sia quello pilotato da ck, mentre i due PMOS saranno interdetti. Quindi il circuito si
configura come mostrato in figura 3.17.
Sistemi sequenziali
177
Fig. 3.16 - Schema a livello transistor del flip-flop a clocked-inverter
Fig. 3.17 - Circuito relativo al flip-flop nel caso in cui ck=ck =1
Notiamo, quindi, che dei due invertitori sono attive soltanto le reti di pull-down. Vediamo allora se,
in queste condizioni, una variazione dell’ingresso D può trasferirsi all’uscita Q (cioè se il nostro
flip-flop è trasparente). Supponiamo che D (in questo intervallo di tempo) passi da 1 a 0,quindi il
potenziale sul nodo M, inizialmente è a 0V. Quando D passa da 1 a 0, l’NMOS s’interdice ed il
PMOS entra in conduzione; il nodo M, quindi, rimane a 0V, e la variazione dell’ingresso non si
trasmette in uscita. Consideriamo il caso in cui D passi da 0 ad 1; inizialmente, quindi, possiamo
supporre che la capacità al nodo M è carica a Vdd. In seguito alla transizione di D tale capacità può
scaricarsi attraverso l’NMOS in conduzione. Quindi la variazione di D ha alterato la carica sulla
Capitolo 3
178
capacità del nodo M; ciò però non modifica il valore dell’uscita. Infatti, essendo tale capacità
inizialmente carica, manteneva in conduzione l’NMOS a valle, e quindi la capacità del nodo
d’uscita era inizialmente scarica. Il fatto che si scarichi la capacità del nodo M (in seguito alla
transizione 0Æ1 su D) fa entrare in conduzione il PMOS a valle, ma ciò non può alterare il valore
dell’uscita (essendo interdetto il PMOS comandato da ck).
Quindi grazie al fatto che sono attive le due sole reti di pull-down non è possibile mai trasferire un
segnale dall’ingresso D all’uscita Q. Quindi, il nostro flip-flop non è trasparente alle transizioni di
D anche quando sia ck che ck sono entrambi pari ad 1.
Un discorso analogo può essere fatto anche quando sia ck che ck sono entrambi pari ad 0; in questo
caso condurranno le due reti di pull-up del circuito; e con un ragionamento analogo è possibile
verificare che il circuito non è mai trasparente alle variazioni di D.
La struttura a clocked-inverter, quindi, da questo punto di vista è da preferire quando si realizza un
flip-flop dinamico. Tale struttura, però, non risolve del tutto i nostri problemi.
Consideriamo, infatti, i due segnali ck e ck (Fig. 3.18), che in generale saranno ritardati fra loro
Fig. 3.18 - Diagramma temporale dei segnali ck e ck
Idealmente il nostro flip-flop dovrebbe essere triggerato sul fronte di discesa del clock (dato che lo
slave diventa trasparente quando il clock diventa basso). Si presenta allora il problema di
identificare l’istante in cui il sistema dovrebbe commutare: è l’istante in cui ck si abbassa oppure
l’istante in cui ck si alza? In realtà, se bisogna portare l’uscita a livello logico alto è necessario che
il segnale di clock si abbassi, dato che entrare in conduzione il relativo PMOS; quindi la transizione
0Æ1 di Q è comandata dal fronte di discesa di ck. Viceversa la transizione 0Æ1 di Q avverrà in
corrispondenza del fronte di salita di ck.
Quindi, seppure questo circuito non è trasparente negli intervalli di sovrapposizione, in linea di
principio non si sa quando può variare l’uscita, se in corrispondenza del fronte di discesa di ck
oppure del fronte di salita di ck. Pertanto se supponiamo di utilizzare come fronti di riferimento
quelli di discesa del clock, in linea di principio il tq del nostro flip-flop include anche il tempo di
overlap fra ck e ck (dato che l’uscita può non variare finché non si alza ck).
Per risolvere del tutto questo tipo di problemi sono stati introdotti recentemente altri tipi di flip-flop
Sistemi sequenziali
179
(e quindi latch) dinamici che presentano la caratteristica di non richiedere il segnale ck, ma
richiedono soltanto l’utilizzo di un segnale di clock. Tali circuiti, quindi, sono a “vera” singola fase
di clock (True Single Phase Clock, TSPC).
Si parte dalla struttura del clocked-inverter eliminando il PMOS pilotato da ck (Fig. 3.19).
Fig. 3.19 - Passaggio da un clocked-inverter ad un half-latch
Questo circuito, a volte, viene chiamato “mezzo latch” (half-latch) perché mettendo in cascata due
di questi circuiti si ottiene un latch; infatti si ha il circuito mostrato in figura 3.20.
Fig. 3.20 - Latch TSPC (trasparente per ck=l, in hold per ck=0)
Verifichiamo allora che il funzionamento di questo circuito è quello di un latch dinamico, ovvero
che quando il clock è alto il circuito è trasparente e quando il clock è basso il circuito è in fase di
hold. Se ck=1, i due NMOS pilotati dal clock sono in conduzione ed il circuito si configura come la
cascata di due invertitori; quindi, ogni variazione di D la si ritrova su Q, ovvero il circuito in questa
Capitolo 3
180
fase è trasparente. Se ck=0 sono interdette entrambe le reti di pull-down del circuito; ci si trova,
quindi, nella stessa situazione del circuito precedente, ovvero del flip-flop realizzato a clockedinverter.
Fig. 3.21 - Circuito del latch TSPC per ck=0
Poiché sono attive soltanto le due reti di pull-up, una variazione dell’ingresso non può dar luogo ad
una variazione dell’uscita. In questa fase, quindi, il latch è in fase di hold. Infatti, quando il clock è
uguale a 0 il circuito si configura come mostrato in figura 3.21. Se D ha una transizione da 1 a 0, il
primo PMOS può entrare in conduzione, caricando la capacità al nodo M, avendola supposta
inizialmente scarica. Ciò, però, non può modificare il valore dell’uscita Q; infatti, l’unica cosa che
accade è che il secondo PMOS si interdice, il che non può alterare il valore memorizzato sull’uscita
Q. Analogamente se D ha una transizione da 0 ad 1 il primo PMOS si interdice, ma ciò non altera
nemmeno lo stato di carica della capacità al nodo M.
Fig. 3.22 - Latch TSPC (trasparente per ck=0, in hold per ck=l)
Sistemi sequenziali
181
Possiamo allora realizzare il duale dei circuito precedente, cioè un latch che è trasparente per ck=0
ed in fase di hold per ck=1, sempre senza utilizzare il segnale ck. Il circuito che si ottiene, allora, è
quello mostrato in figura 3.22. Mettendo allora in cascata questi due latch (quelli di figura 3.20 e
3.22) realizziamo un flip-flop TSPC.
Oltre ai circuiti appena visti esistono delle versioni ulteriormente semplificate che fanno uso di un
numero ridotto di dispositivi. Queste versioni prendono il nome di latch, e quindi anche flip-flop,
con split-output (ovvero con uscite suddivise).
Un latch con split-output è fatto come mostrato in figura 3.23; è costituito da half-latch in cui sono
sfruttati sia il morsetto di dram che quello di source dell’NMOS pilotato da ck, i quali pilotano
l’NMOS ed il PMOS dello stadio a valle, il quale non necessita di pilotaggio di clock. Il principio di
funzionamento di questo latch è semplicemente un’estremizzazione di quello visto finora, ovvero
che se abbiamo due reti di pull-down (o di pull-up attive), il circuito non è mai trasparente.
Fig. 3.23 - Latch con split-output
In questo caso, infatti, se ck=1 il circuito è ovviamente trasparente, dato che si configura come un
buffer. Per ck=0 l’NMOS pilotato dai clock si interdice; si hanno allora due stadi in cascata, in cui
la rete di pull-up del primo comanda la rete di pull-up del secondo, e la rete di pull-down del primo
comanda la rete di pull-down del secondo. Anche in questo caso, allora, una qualsiasi variazione
dell’ingresso non potrà mai dar luogo ad una variazione dell’uscita. Se, ad esempio, consideriamo la
capacità C1, al variare dell’ingresso essa può al più scaricarsi; nel momento in cui si scarica
l’NMOS a valle si interdice, ma ciò non varia in alcun modo l’uscita; un discorso analogo si può
fare per la capacità C2 (notiamo che il circuito, per quanto sia un latch, sfrutta in realtà tre capacità,
C1, C2 e C3).
Un primo vantaggio di questa struttura rispetto alla precedente, anche se non molto significativo, è
Capitolo 3
182
che c’è un transistore in meno. Invece il vantaggio principale è che il carico sul clock è ridotto al
massimo, infatti il clock è collegato ad un solo mosfet. Quindi la capacità sul clock è molto bassa e
la potenza dissipata per comandare il segnale di clock è molto ridotta; inoltre, se è ridotta la capacità
sul clock anche i ritardi introdotti dalle interconnessioni relative ai clock si riducono (quindi anche
il problema del clock-skew viene a mitigarsi). In realtà, l’unico piccolo svantaggio di questo
circuito rispetto al precedente èlegato al fatto che l’escursione logica del nodo M” è O÷(Vdd-VT),
ciò significa che l’NMOS a valle non si porta mai al pieno della conduzione; quindi, da questo
punto di vista, il circuito può essere considerato leggermente più lento. Inoltre questo tipo di circuiti
sono delicati, in quanto l’uscita può trovarsi in una condizione per cui lo stato è mantenuto dalla
capacità C3 (ovvero è un soft-node), ma questa uscita è pilotata da un PMOS che a sua volta ha sulla
gate un altro soft-node. Quindi se c’è un piccolo accoppiamento capacitivo fra questi nodi,
soprattutto quelli interni (M’ ed M”), ed altre linee del nostro circuito, ciò può alterare la
conduzione o l’interdizione dei relativi mosfet, e alterare lo stato di carica della capacità d’uscita.
Da questo punto di vista, dunque, il circuito è più sensibile ad accoppiamenti parassiti fra questi
soft-node ed altre linee del circuito integrate, ovvero ai cosiddetti problemi di cross-coupling.
Possiamo allora realizzare un flip-flop collegando in cascata due latch con split-output, come
mostrato in figura 3.24. Inoltre è possibile dimostrare che una versione ottimizzata di questo flipflop è quella che si ottiene da questo circuito eliminando il secondo stadio del primo latch e
collegando direttamente i nodi A e B, rispettivamente, al PMOS e all’NMOS del primo stadio del
secondo latch.
Questi circuiti, quindi, vengono utilizzati nelle applicazioni più avanzate, laddove serve la massima
velocità e la massima sicurezza rispetto ai problemi di sovrapposizione delle diverse fasi di clock.
Fig. 3.24 Flip-flop con split-output
Sistemi sequenziali
3.4
183
Pipelining
Supponiamo di avere un sistema fatto nel modo mostrato in figura 3.25; abbiamo un segnale
d’ingresso A su n bit, un primo banco di registri piotati dal segnale di clock, sulla cui uscita
effettuiamo delle elaborazioni attraverso la cascata di tre stadi combinatori F,G ed H. L’uscita di
quest’ultimo stadio viene memorizzata in un secondo banco di registri. Tutti i flip-flop, come in
ogni buon sistema sincrono, sono pilotati dallo stesso segnale di clock, anzi si farà in modo che tale
segnale di clock arrivi quanto più possibile contemporaneamente a tutti i registri.
Fig. 3.25 – Sistema tipico cui applicare il pipelining
Valutiamo la frequenza massima, ovvero il periodo minimo del nostro segnale di clock. Esso sarà
legato ad aspetti di non idealità dei registri, cioè il tempo tq del primo registro ed il tempo ts del
secondo, ed alla somma dei tempi di ritardo dei vari sistemi combinatori, ovvero risulta:
Tmin = tq +ts+tpF+tpG+tpH
In prima approssimazione, se supponiamo che i ritardi dominanti siano quelli dei blocchi
combinatori, si ha:
Tmin ≅ tpF+tpG+tpH
Inoltre, se supponiamo che questi tre ritardi siano uguali ovvero: tpF=tpG=tpH=tp,comb, il periodo
minimo è Tmin ≅ 3 tp,comb.
Proviamo allora a modificare il nostro circuito introducendo il concetto di pipelining. Si introduce il
pipelining nel nostro sistema “spezzando” il nostro sistema combinatorio ed introducendo dei
registri, detti regtstri di pipelining. Ad esempio, possiamo pensare di spezzare il nostro sistema
combinatorio tra i blocchi F e G e fra G ed H, come mostrato in figura 3.26.
Fig. 3.26 – Introduzione del pipelining nel sistema combinatorio
Capitolo 3
184
Verifichiamo adesso che il funzionamento di questo circuito è lo stesso di quello originario; a tale
scopo consideriamo il diagramma temporale di figura 3.27.
Fig. 3.27 – Diagramma temporale del sistema pipelined
Supponiamo, ad esempio, che tutti i registri siano triggerati sul fronte di discesa del clock; quindi,
sul segnale ck evidenziamo i fronti attivi. Supponiamo che il primo valore dell’ingresso, A1, venga
catturato in corrispondenza del primo fronte del clock; dopodiché cambiamo l’ingresso mettendo un
nuovo valore A2, poi A3, A4, e così via. Ovviamente A deve variare con un certo margine rispetto
ai tempi di setup e di hold dei registri. L’ingresso xF del blocco combinatorio F, dopo un ritardo dal
primo colpo di clock pari al tq dei flip-flop, assumerà il valore Al; dopo il secondo colpo di clock
assumerà il valore A2, poi A3, e così via. Il blocco F effettuerà la sue elaborazioni e la sua uscita yF
si dovrà assestare prima che si abbia il successivo fronte attivo del clock; avremo dunque, con un
certo ritardo dal primo fronte attivo del clock, il va1ore F(A1), poi F(A2), F(A3), e così via. Per
quanto riguarda l’ingresso del blocco G, abbiamo che in corrispondenza del secondo fronte del
clock possiamo catturare l’uscita elaborata dal blocco F, cioè F(A1); in corrispondenza dei
successivi fronti del clock sarà poi catturato F(A2), F(A3), e così via.
Notiamo quindi che nel periodo successivo al primo fronte del clock viene catturato Al ed il blocco
F comincia ad elaborare questo primo vettore d’ingresso. Nel periodo successivo accadono
contemporaneamente due cose: cambiamo l’ingresso del blocco F, che comincia già ad elaborare
l’ingresso A2, e contemporaneamente il blocco G elabora il risultato della precedente elaborazione,
cioè elabora F(A1).
Questo processo prosegue fino a quando non si “riempie” tutta la pipeline; quindi, per avere il
primo risultato utile bisogna aspettare 4 colpi di clock (necessari per caricare i quattro registri con i
valori utili). Questo ritardo, necessario per avere la prima uscita utile, prende il nome di latenza,
Sistemi sequenziali
185
ovvero c’è una latenza iniziale nel nostro sistema pipelined.
Mentre nel sistema precedente era necessario un colpo di clock per caricare il primo registro ed un
secondo colpo di clock per avere la prima uscita, nel sistema pipelined sono necessarie due fasi di
clock aggiuntive, avendo aggiunto due registri intermedi. Quindi, l’introduzione dei registri di
pipelining ha aumentato la latenza di due colpi di clock.
Il vantaggio significativo della struttura pipelined è che si ha un’uscita ad ogni colpo di clock, e la
frequenza di clock può essere aumentata significativamente rispetto al sistema originario; infatti, in
questo caso, fra un registro e l’altro c’è un solo blocco combinatorio, non più tre. Quindi, in questo
caso il periodo minimo del clock è in generale dato da:
Tmin = max (tpF,tpG,tpH)
ovvero dal massimo dei ritardi dei vari blocchi combinatori. Quindi è chiaro che l’introduzione del
pipelining è tanto più efficace. quanto più possiamo bilanciare i ritardi, ovvero se tpF=tpG=tpH sono
uguali fra loro; in tal caso si riesce addirittura a migliorare di un fattore3 la frequenza di clock.
Il problema che si presenta, però, è che questo miglioramento della frequenza di clock viene a
discapito di una latenza. Ci sono, allora, delle applicazioni in cui questa latenza è accettabile, cioè
non è un vero problema, ed altre in cui viceversa ciò non accade. Un esempio di applicazione in cui
la latenza non comporta problemi è quello di un processing digitale di segnali; se abbiamo dei
segnali che sono stati catturati con un convertitore A/D e dobbiamo effettuare un filtraggio
numerico (ovvero bisogna effettuare dei prodotti di convoluzione, quindi somme e prodotti)
possiamo utilizzare i registri di pipelining. In questo caso la latenza comporta un ritardo dall’istante
in cui si ha il primo campione in ingresso all’istante in cui si ha la prima uscita utile; ciò, però non è
un problema nel processo dei segnali. Il fatto di poter aumentare la frequenza di clock invece è
fondamentale, in quanto sappiamo che essa deve essere almeno il doppio rispetto alla banda dei
segnale; quindi s si riesce ad aumentare la frequenza di clock significa che possiamo elaborare
segnali a frequenza maggiore, e quindi aumentare il campo delle nostre applicazioni.
Viceversa questa latenza può non essere accettabile in altre applicazioni. Ad esempio, se abbiamo
un’unità logico/aritmetica (che stiamo introducendo all’interno di un microprocessore) possiamo
scomporla in tanti sotto-blocchi, a cui pensiamo di applicare il pipelining. Se l’ALU eseguisse
sempre la stessa operazione (ad esempio, delle somme) allora sarebbe una buona idea introdurre il
pipelining, dato che aumentando la frequenza di clock le somme verrebbero effettuate ad una
frequenza maggiore; la latenza iniziale non comporterebbe alcun tipo di problema. Il problema
invece nasce se, come accade, l’ALU a volte deve eseguire delle somme, a volte delle operazioni
logiche, e così via.. In questo caso non e possibile intervallare delle operazioni differenti con i vari
blocchi; bisognerà aspettare tutta la latenza per avere il primo risultato utile, poi bisogna mettere in
stallo la pipeline, mettere poi il nuovo ingresso ed aspettare di nuovo tutta la latenza. In questo caso,
quindi, non si ha alcun particolare vantaggio dall’utilizzo del pipelining; il vantaggio lo si ha
quando si deve effettuare sempre la stessa sequenza di operazioni.
Anche all’interno dei microprocessori, dato che in realtà il ciclo di operazioni è quasi sempre lo
stesso (si prende un codice operativo dalla memoria, si aggiustano gli operandi e si effettua
Capitolo 3
186
l’operazione desiderata), è utile avere un concetto di pipelining. Cioè, mentre si esegue una certa
operazione, si cominciano già a prelevare gli operandi dell’operazione successiva. Però, anche in
questo caso, quasi sempre tale pipelining va bene; in alcuni casi l’operazione che bisogna effettuare
può essere un’operazione di salto. Quindi, mentre si elabora una certa operazione non si sa se la
prossima operazione sarà quella successiva o se, dovendo effettuare un salto, bisogna prelevare
questa operazione in qualche altra locazione di memoria. In questo caso, riconoscendo
un’operazione di salto, si può procedere mettendo in stallo la pipeline; quindi, si aspetta prima di
compiere o meno il salto, prima di accedere in memoria. Oppure si può andare avanti nella pipeline,
ipotizzando che il salto non venga effettuato; poi, se alla fine doveva essere effettuato il salto, si
scarteranno alcuni risultati e si riprenderanno certe operazioni.
3.5
Esempi di applicazione del pipelining
Consideriamo un addizionatore a propagazione del riporto (Fig. 3.28) su tre bit. Sappiamo che c’è
un cammino critico, che va dal primo all’ultimo full-adder, a causa del quale l’addizionatore è
abbastanza lento. Tuttavia, tale struttura risulta essere costituita da un certo numero di moduli in
cascata, per cui ben si presta ad essere migliorata introducendo la tecnica del pipelining.
Fig. 3.28 - Addizionatore a propagazione del riporto
Per semplicità, nello schema dell’addizionatore pipelined, rappresenteremo i registri di memoria
con una linea ed un pallino sopra (—•—); l’ingresso, ovviamente, sarà sulla sinistra, l’uscita sulla
destra ed il clock è lo stesso per tutti i registri. Otterremo pertanto il circuito di ‘figura 3.29
Partendo dal primo full-adder, gli ingressi A0, B0 e C0 saranno memorizzati su dei flip-flop, le cui
uscite vengono applicate al primo full-adder. Dopo un tempo pari al ritardo del full-adder possiamo
catturare le uscite; quindi, sia su S0 che sul riporto uscente inseriamo un flip-flop. Per quanto
riguarda il secondo full-adder, sugli ingressi A1 e B1 ci saranno dei flip-flop allo stesso livello di
quelli su A0 e B0. Inoltre, ci sarà un secondo livello di flip-flop per far si che al full-adder si
Sistemi sequenziali
187
presentino gli ingressi giusti, ovvero A1, B1 ed il riporto uscente dello stadio precedente (che sarà
disponibile dopo due colpi di clock). Introdurremo poi un registro sul riporto uscente di questo fulladder e sull’uscita S1. Osserviamo però che bisogna aggiungere un altro quando sarà disponibile
l’uscita S1 (dopo tre colpi di clock), perderemo il valore del primo bit somma. Per quanto riguarda il
terzo full-adder è semplice intuire dove posizionare i registri; basta seguire i tagli (linee tratteggiate)
riportati in figura ed inserire un registro in corrispondenza dell’intersezione di queste linee con i
vari segnali. Notiamo che bisogna aggiungere due ulteriori registri, uno sull’uscita S1 e l’alto
sull’uscita S0.
Fig. 3.29 - Addizionatore pipelined
Quindi per realizzare il pipelining bisogna introdurre delle sezioni che separano completamente gli
ingressi dalle uscite, ed introdurre un flip-flop per ognuna di queste sezioni. Notiamo come, in
questo modo, alcuni flip-flop saranno in serie sugli ingressi mentre altri saranno in serie sulle uscite.
Lo scopo di ciò, ovviamente, è quello di avere i segnali giusti al momento giusto. La prima uscita
utile la si otterrà dopo quattro colpi di clock.
Il periodo minimo (ovvero la frequenza massima) del segnale di clock sarà dato da:
Tmin = ts+tq+max(tp,sum,tp,carry)
Quindi un progetto ottimale del full-adder, al fine di utilizzato in una struttura pipelined, è quello
per cui tp,sum ≅ tp,carry; infatti, in tal caso, non ha molto senso privilegiare un’uscita rispetto all’altra.
Osserviamo inoltre che se effettuiamo un pipelining per ogni full-adder, il termine ts+tq comincia ad
essere comparabile con il tempo di ritardo del full-adder. Ciò ci suggerisce, allora, che ad un certo
punto non conviene proseguire con la tecnica del pipelining, in quanto entreranno in gioco i ritardi
del flip-flop, che saranno quelli che limiteranno la velocità di funzionamento del circuito. Possiamo
allora pensare di realizzare il pipelining non ogni full-adder, ma ogni due full-adder; ciò è possibile
semplicemente eliminando i registri sulla linea (*) indicata in figura. In questo caso si interpongono,
fra un flip-flop e l’altro, due full-adder; si riducono le prestazioni ma si risparmiano anche 6 registri.
Capitolo 3
188
Essendo una struttura modulare saremo noi a decidere come realizzare il pipelining, in funzione
delle prestazioni che bisogna raggiungere.
Osserviamo che si potrebbe pensare che l’ultimo livello di registri sulle uscite dell’addizionatore
possa essere eliminato (togliendo, quindi, il flip-flop su S2, ed uno su S1 ed S0); in realtà, però, ciò
dipende dal circuito che sarebbe collegato a valle dell’addizionatore. Consideriamo, infatti il
sistema mostrato in Figura 3.30, in cui abbiamo l’addizionatore pipelined (che somma A e B), un
comparatore, che darà un’uscita alta se i due ingressi W e C sono uguali, ed un flip-flop in cui viene
memorizzato il risultato del confronto.
Fig. 3.30 - Esempio di sistema in cui viene utilizzato l’addizionatore
Il periodo del clock, allora, dipenderà dal ritardo combinatorio di questo flip-flop ed il registro
precedente. Se mettiamo un registro su tutte le uscite dell’addizionatore sull’ingresso C, il ritardo
che bisogna considerare è quello del comparatore (tcomb); se invece mettiamo un registro solo sugli
ingressi, il ritardo che bisogna considerare è la somma del ritardo del comparatore più quello
dell’addizionatore. Se, nell’addizionatore pipelined non mettiamo il registro sull’ultima uscita S2
(ovvero non mettiamo l’ultimo livello di registri), bisogna considerare il ritardo del comparatore più
il ritardo di un full-adder. In generale, quindi, è buona norma mettere un registro alla fine di un
blocco combinatorio.
3.6
Esempi di sistemi sequenziali
Consideriamo, ad esempio, un addizionatore seriale; esso è un circuito abbastanza semplice che
sfrutta un unico full-adder.. Gli ingressi A e B sono forniti serialmente, inviando prima il bit meno
significativo, A0 e B0, poi A1 e B1, e così via (Fig. 3.31). Tutti questi valori vengono memorizzati in
un registro a scorrimento; quindi, dopo tre colpi di clock avremo nel primo registro, A0, nel secondo
A1 e nel terzo A2.
A questo punto il full-adder è pronto per effettuare la somma fra A0 e B0; ci sarà anche un riporto
entrante, memorizzato anch’esso in un flip-flop, che deve però essere inizialmente resettato. Quindi,
Sistemi sequenziali
189
inizialmente, viene fatta la somma fra A0, B0 e 0; il risultato S0 viene salvato in un registro ed il
riporto, C0, viene memorizzato nel flip-flop del riporto per essere sommato ad i successivi bit (A1 e
B1). Al colpo di clock successivo, quindi, si sommano A1, B1 e C0. In questo modo si calcola S1 e,
per non perdere S0, si mette un secondo registro in uscita; in questo modo S0 passa al registro
successivo e S1 viene memorizzato nel primo registro.
Fig. 3.31 - Addizionatore seriale a 3 bit
Al successivo colpo di clock vengono sommati A2, B2 e C1 la somma S2 viene memorizzata nel
primo registro, S1 passa nel secondo ed S0 in un terzo registro. Notiamo, quindi, che con un
addizionatore a 3 bit sono necessari 3 colpi di clock per ottenere il risultato utile (nell’ipotesi che i
registri a scorrimento in ingresso siano già stati caricati). Inoltre è necessario un solo full-adder,
dato che il riporto viene salvato in un flip-flop per utilizzarlo al colpo di clock successivo. Tale
struttura è ben diversa dalla struttura pipelined vista nel paragrafo precedente dato che, in questo
caso, la struttura è seriale. Bisogna caricare prima gli ingressi A e B, poi vengono effettuare le
operazioni di somma, e poi si ottengono le uscite un bit alla volta. Se l’addizionatore è ad n bit,
bisogna aspettare almeno n colpi di clock prima di avere il risultato della somma. Inoltre, prima di
effettuare una nuova somma, bisogna resettare il flip-flop del riporto, dopodiché ci vorranno altri n
colpi di clock per avere la nuova somma. Quindi, sotto certi aspetti, questa struttura è esattamente
l’opposto di quella pipelined; non abbiamo un risultato ad ogni colpo di clock, ma ce ne vorranno n.
Pertanto, nella struttura seriale, si introducono i registri non per aumentare la velocità del sistema
ma per ridurne la complessità (risparmio di area): Anche questa struttura non è utilizzabile in un
microprocessore; invece è una scelta che si può utilizzare quando bisogna elaborare dei dati (con un
circuito di elaborazione numerica di segnali) che arrivano ad una frequenza abbastanza bassa
rispetto alla possibile frequenza di clock. Pertanto, non ha senso fare un addizionatore parallelo
molto veloce; per risparmiare area, è preferibile utilizzare un addizionatore seriale.
Un altro esempio di sistema sequenziale è un contatore, un sistema, che ad ogni colpo di clock
fornisce un’uscita crescente (0, 1, 2 e cosi via), ovviamente codificata in binario. Tale circuito può
essere semplicemente realizzato come in figura 3.32.
Basta utilizzare un banco di registri in cui l’uscita è lo stato attuale, x, e l’ingresso è lo stato futuro,
y, che non sarà altro che x+l; quindi bisogna utilizzare un addizionatore che somma sempre 1,
ovvero un addizionatore in cui un addendo è zero, l’altro è x e sfruttiamo il riporto entrante (Cin=1)
Capitolo 3
190
per sommare un’unità al nostro contatore. Per il banco di registri è opportuno, inoltre, prevedere
anche un ingresso di reset; quindi, inizialmente lo si pone a zero e poi si ha un incremento di 1 ad
ogni colpo di clock.
Fig. 3.32 Schema di un contatore
Entrando più in dettaglio nella struttura dell’addizionatore utilizzato in questo caso, facciamo
riferimento alla figura 3.33, in cui è stata usata una struttura a propagazione del riporto.
Fig.. 3.33 - Schema del contatore: stuttura dell’addizionatore
Ognuna delle bit-slice in cui si può decomporre questa struttura sarà costituita come mostrato in
figura 3.34, ovvero composta da un full-adder ed un registro.
Fig.. 3.34 - Bit –slice del contatore: stuttura dell’addizionatore
Sistemi sequenziali
191
Dato che uno degli ingressi del full-adder è sempre zero, analizziamone più a fondo la struttura. Le
equazioni che lo descrivono sono le seguenti:
⎧S = Q ⊕ Cin
⎨
⎩Cout = Q ⋅ Cin
Quindi bisogna semplicemente utilizzare una porta AND ed una XOR per ogni bit-slice. Si ottiene,
quindi, la struttura mostrata in figura 3.35.
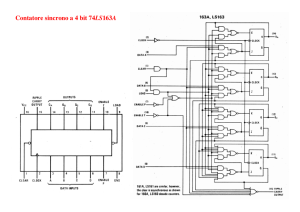
Fig. 3.35 - Schema del contatore:struttura del full-adder di ogni bit-slice
La frequenza massima di conteggio del nostro circuito sarà limitata dal ritardo massimo del sistema
combinatorio. Nel nostro caso, l’addizionatore, per quanto semplificato, è comunque a
propagazione del riporto; quindi, possiamo aspettarci che il ritardo massimo sia quello dovuto alla
propagazione del riporto. In ogni caso il circuito è più semplice di un normale addizionatore dato
che si somma sempre l. Notiamo, inoltre, che il riporto uscente della seconda bit-slice è dato dalla
AND dell’uscita X1, dell’uscita X0, e di Cin. Quindi, anziché ”ottenerlo attraverso due porte AND,
possiamo pensare di modificare il circuito eliminando la AND della seconda bit-slice ed inserendo
una AND a tre ingressi (la XOR della seconda bit slice prenderà il riporto uscente comunque dalla
AND della prima). In questo modo è possibile calcolare in maniera più efficace il riporto uscente
per una data bit-slice.
3.7
Metastabilità e sincronizzatori
Nel caso dei sistemi sequenziali le condizioni che devono essere rispettate perché un circuito
funzioni correttamente sono, sostanzialmente, il rispetto dei vincoli sul tempo di setup e sul tempo
di hold. Poiché all’interno del nostro circuito possiamo valutare i ritardi dei sistemi combinatori che
lo costituiscono, possiamo sempre progettare il sistema in modo tale che questi vincoli siano
perfettamente rispettati.
Il problema però nasce quando esistono degli ingressi al nostro sistema che sono asincroni, che
Capitolo 3
192
provengono dal modo esterno, le cui variazioni non sono in alcun modo legate a quelle del segnale
di clock, che scandisce il funzionamento del nostro sistèma.
Supponiamo che un segnale asincrono a venga inviato all’ingresso D di un flip-flop (Fig. 3.36).
Fig. 3.36 - Flip-flop con ingresso asincrono
Il problema è che su questo segnale asincrono non abbiamo alcun tipo di controllo, le sue
commutazioni possono avvenire in un istante di tempo qualsiasi. Quindi può accadere che il segnale
a vari proprio in prossimità di un fronte attivo del clock (Fig. 3.37) senza rispettare i vincoli di setup
e di hold.
Fig. 3.37 - Variazione di a in prossimità del fronte attivo del clock
Fig. 3.38 - Flip-flop dinamico
Sistemi sequenziali
193
Osserviamo che il comportamento sarà diverso a seconda che il flip-flop sia statico o dinamico.
Supponiamo che il flip-flop sia di tipo dinamico (Fig. 3.38); in questo caso sappiamo che lo stato
del sistema è memorizzato in una carica accumulata sulle capacità presenti nel nostro circuito.
Poiché il segnale a varia proprio in corrispondenza del fronte attivo del clock, si può avere una
situazione in cui la tensione immagazzinata su queste capacità (Vc) viene a trovarsi proprio in
corrispondenza della regione proibita della caratteristica di trasferimento dell’invertitore, ovvero
VIL<Vc<VIH. Questo potenziale, quindi, non viene riconosciuto né come livello logico alto né come
livello logico basso. Pertanto l’uscita Q del flip-flop, che inizialmente era bassa, può portarsi ad un
livello di tensione intermedio compreso fra 0 e VDD (illegale dal punto di vista logico). Nel caso di
un flip-flop dinamico, purtroppo, accade che il livello di tensione VC, una volta immagazzinato
sulla capacità, rimane invariato fino a quando non si ha il successivo fronte del clock. In
corrispondenza di tale fronte, supponendo che a abbia raggiunto il livello logico alto, l’uscita si
porterà al valore corretto. Quindi per un registro dinamico, se sono violati i vincoli sul tempo di
setup e di hold, l’uscita Q può portarsi ad un valore logico indefinito, e rimarrà bloccata a tale
valore fino al successivo fronte del clock. In questo caso si dice anche che un registro dinamico non
è in grado di recuperare una condizione di malfunzionamento (a causa delle capacità che rimangono
caricate al valore VC).
Nel caso di un flip-flop statico sappiamo che l’elemento di base è un circuito bistabile che, oltre ai
due punti di equilibrio stabile, presenta un punto di equilibrio instabile.
Fig. 3.39 - Caratteristica di trasferimento di un circuito bistabile
Sappiamo che per ottenere i punti di equilibrio di tale sistema basta spezzare il loop e valutare la
caratteristica fra vi e v0 (Fig. 3.39); i punti .A e B sono di equilibrio stabile, mentre M è di equilibrio
instabile. Pertanto se consideriamo un flip-flop statico può accadere che esso si porti a lavorare in
prossimità del punto di equilibrio instabile; l’uscita Q, anche in questo caso, quindi, si può portare
ad un valore logico indeterminato (Fig. 3.37), corrispondente al fatto che il potenziale relativo al
punto M è esso stesso indeterminato dal punto di vista logico. Poiché, però, c’è un ciclo di reazione
positiva, ed M è un punto di equilibrio instabile, una qualsiasi minima perturbazione al nostro
sistema farà si che l’uscita Q si porti dal punto metastabile o verso il livello logico basso o verso il
livello logico alto (in maniera del tutto casuale, dipendente dal disturbo eventualmente sovrapposto
Capitolo 3
194
al segnale d’ingresso). In questo caso avremo un tempo di metastabilità, tm, trascorso il quale il flipflop è in grado di “risolvere” l’uscita, ovvero l’uscita si porterà ad un valore logico determinato (0
oppure 1).
In definitiva, vi e un differente comportamento fra un flip-flop dinamico ed uno statico; per il primo
l’uscita, portatasi nello stato illegale, vi rimane fino al successivo fronte del clock. Il flip-flop
statico, grazie al fatto che M è un punto di equilibrio instabile, può risolvere l’uscita in un tempo tm
se c’è una minima perturbazione sovrapposta al segnale (in corrispondenza del punto M). Nel caso
dei flip-flop dinamici il tempo di metastabilità è pari al periodo del segnale di clock per i flip-flop
statici, invece, questo tempo tm vedremo come può essere calcolato, ma in linea di principio può
senz’altro essere più basso del periodo del clock.
Pertanto dei due tipi di flip-flop, il più adatto ad essere utilizzato come sincronizzatore è certamente
quello statico, dato che è in grado da solo di risolvere in qualche modo l’uscita; i flip-flop dinamici
non sono adatti per essere utilizzati come sincronizzatori. Osserviamo che anche se l’uscita del flipflop statico non si porta al livello logico corretto dopo il tempo tm, ciò non comporta alcun problema
dato che al successivo fronte del clock, con un buon margine sui tempi di setup e di hold, verrà
individuato il valore logico corretto (quello alto, nel nostro esempio). In questo caso, quindi, ci si
accorge della variazione del segnale asincrono con un ritardo pari al periodo del clock. Ciò però non
è un problema perché sicuramente la frequenza del segnale di clock è sufficientemente maggiore
rispetto a quella del segnale asincrono esterno (altrimenti, non avrebbe senso campionario alla
frequenza di clock).
L’importante, quindi, è che il flip-flop non rimanga troppo a lungo nello stato metastabile.
Consideriamo, infatti, il sistema mostrato in figura 3.40, in cui abbiamo il segnale asincrono a in
ingresso ad un flip-flop che funziona da sincronizzatore, la cui uscita viene inviata in ingresso ad un
sistema sequenziale.
Fig. 3.40 - Sistema sequenziale con ingresso proveniente da un sincronizzatore
Sistemi sequenziali
195
Il problema che si presenterebbe, se il segnale Qa si trovasse ad un potenziale cui corrisponde un
livello logico indefinito, è che due porte logiche potrebbero interpretare questo segnale l’una come
livello logico alto e l’altra come livello logico basso. Ciò comporta che lo stato futuro in cui si va a
posizionare il sistema sia uno stato che non è stato previsto quando è stata progettata la nostra
macchina sequenziale. Ciò, ad esempio, potrebbe comportare che il sistema vada a porsi in uno
stato da cui non è più in grado di uscire; da questo errore di sincronizzazione, quindi, potrebbe non
essere più possibile recuperare il funzionamento del sistema.
Vediamo, quindi, come sia possibile porre rimedio a questo problema. Innanzitutto è ovvio che
bisogna considerare, come sincronizzatore, un flip-flop statico; valutiamo allora qual è il massimo
tempo di metastabilità, tm,max, che è possibile tollerare all’uscita di questo flip-flop. A tale scopo
consideriamo il diagramma temporale di figura 3.41, in cui il segnale asincrono varia proprio in
corrispondenza del fronte del clock.
Fig. 3.41 - Diagramma temporale per la valutazione del tm,max
L’uscita Qa del sincronizzatore passa in uno stato metastabile per un tempo tm, dopo il quale si
porta, in maniera casuale, a 0 oppure ad 1; al fronte successivo del clock, in ogni caso, viene
individuato il valore corretto di Qa. L’uscita y, stato futuro del nostro sistema sequenziale, potrà
essere elaborata dal nostro sistema combinatorio certamente non in corrispondenza del primo fronte
del clock; bisogna attendere prima che Qa assuma il valore corretto, e poi bisogna considerare il
ritardo del sistema combinatorio. Per avere dunque un corretto funzionamento del nostro sistema
deve risultare:
T ≥ tm+tc,max+ts
Quindi, in pratica, il tempo di metastabilità può essere visto come un incremento del ritardo tq del
primo flip-flop. Da questa relazione si ricava che il massimo tempo di metastabilità che è possibile
Capitolo 3
196
tollerare è dato da:
tm, max = T - tc,max - ts
Da questa relazione si ricava che se il tempo di metastabilità è minore di tm,max il nostro sistema
funzionerà correttamente, dato che l’uscita dei registri viene campionata con un margine sufficiente
rispetto al fronte del clock. Se invece questo periodo di metastabilità è maggiore di tm,max, il sistema
sequenziale potrebbe non funzionare correttamente, dato che per le uscite non sarebbero più
rispettati i vincoli sul tempo di setup e di hold. Questa relazione, inoltre, Ci conferma che non è
possibile utilizzare un flip-flop dinamico come sincronizzatore dato che per esso tm=T. Per un flipflop statico, invece, è possibile calcolare tm e valutare in quali condizioni questo tempo è maggiore
o minore di tm,max.
Per avere una stima di trn facciamo delle ipotesi semplificative; supponiamo che il segnale di clock
sia ideale (quindi con tr=tf=0) e che il segnale d’ingresso a abbia dei tempi di salita e di discesa
diversi da zero, come mostrato in figura 3.42.
Fig. 3.42 - Andamenti di ck ed a per la stima di tm
Inoltre supponiamo che il fiip-flop statico si comporti, in qualche modo, come un circuito
Sample&Hold, ovvero come un campionatore la cui uscita vq all’istante 0 sia pari alla tensione
d’ingresso va a t=0, ovvero vq(0)=va(0). Quindi il valore iniziale che si ha sull’uscita è perfettamente
uguale al valore d’ingresso campionato in corrispondenza del fronte attivo del clock. Bisogna, a
questo punto, definire la legge con cui questa uscita varia nel tempo. Se il flip-flop fosse stato
dinamico l’uscita, come sappiamo, resterebbe bloccata al valore vq(0). Poiché il flip-flop è statico
l’uscita parte da vq(0) e poi tenderà o verso VDD o verso 0, secondo una legge che ipotizziamo
essere la seguente:
vq(t) = VM +(vq(0)- VM)et/τ
Sistemi sequenziali
197
in cui VM è la tensione di metastabilità, cioè quella che corrisponde al punto di equilibrio instabile
(del circuito costituito dai due invertitori in retroazione).
Quindi il nostro flip-flop campiona inizialmente il valore dell’ingresso in corrispondenza del fronte
attivo del clock; se questo valore è leggermente più grande di VM si ha un andamento con un polo a
parte reale positiva, quindi con una costante di tempo τ tale per cui l’uscita diverge, tendendo
idealmente a +∞. Ovviamente l’uscita è limitata dal fatto che non può superare il valore della VDD e,
quindi, la traiettoria che ci aspettiamo è quella mostrata in figura 3.42. Questa legge deriva dal fatto
che essendo il punto di equilibrio instabile abbiamo un polo a parte reale positiva; se vq(0) è molto
prossimo a VM avremo sempre questo andamento divergente, però il coefficiente del termine
esponenziale è piccolo e quindi il tempo necessario per risolvere l’uscita tende ad aumentare.
In base a questo modello (molto semplificato, ma che ci consente di stimare tm) si deduce che se
viene campionato l’ingresso proprio quando la tensione è pari a VM, l’uscita resterebbe bloccata per
un tempo indefinito al valore VM. Se invece vq(0) è più piccolo di VM il coefficiente
dell’esponenziale è negativo e l’andamento è decrescente, come mostrato in figura 3.42. Il tempo
necessario per risolvere l’uscita è, ovviamente, tanto minore quanto più vq(0) è lontano da VM.
Per il calcolo di tm supponiamo vq(0) > VM, la traiettoria dell’uscita sarà del tipo mostrato in figura
3.43. Per valutare tm bisogna individuare il valore di VIH; infatti quando la tensione d’uscita del flipflop supera tale valore l’uscita sarà al livello logico alto.
Fig. 3.43 - Traiettoria dell’uscita per vq(0) > VM,
Osserviamo però che non si commette un grosso errore se si approssima VIH con VDD, inoltre si fa
l’ulteriore ipotesi semplificativa che VM=VDD/2. Da ciò si ricava che:
v q (t m ) = V DD ⇒ VM + (v q (0 ) − VM )e
tm
τ
V
V ⎞ m
⎛
⇒ DD + ⎜ v q (0 ) − DD ⎟e τ = VDD
2
2 ⎠
⎝
t
= VDD
t
⎤
⎡
VDD ⎞ τm VDD
VDD / 2
⎛
⎥
⇒ t m = τ log ⎢
⇒ ⎜ v q (0 ) −
⎟e =
2 ⎠
2
⎝
⎢⎣ v q (0) − VDD / 2 ⎥⎦
Notiamo che tali relazioni valgono anche nel caso in cui vq(0) < VM; pertanto l’espressione di tm
ottenuta, mettendo il valore assoluto al denominatore, vale in entrambi i casi.
Capitolo 3
198
Per valutare in quali condizioni il tm appena calcolato può diventare più grande di tm,max, facciamo
riferimento al diagramma temporale di figura 3.44, in cui riportiamo il segnale di clock e la tensione
d’ingresso va.
Fig. 3.44 - Errore di sincronizzazione: fascia di valori proibiti intorno a VM
Se va(0)<VM sicuramente si avrà un problema di metastabilità (addirittura, dalla relazione
precedente, tm tende all’infinito); in realtà esiste una fascia di valori proibiti intorno a VM, di
ampiezza 2vε, per i quali tm > tm,max, e, quindi, si ha un errore di sincronizzazione. Dal punto di vista
del progetto, è chiaro che se possiamo agire su qualche parametro progetteremo il nostro sistema in
modo da rendere la vε, quanto più piccola possibile, in modo da ridurre al massimo la probabilità di
un errore di sincronizzazione. Dunque la vε è data da:
t m,max
t
⎧ tτm
VDD /2
VDD /2
VDD − m,τmax
τ
e
⇒e
=
⇒ vε =
⎪e =
v
(0)
V
/2
v
2
−
⎨
a
DD
ε
⎪t = t
m, max
⎩m
Osserviamo che è importante sia che il flip-flop sia veloce, quindi una τ quanto più piccola
possibile, sia che la vε sia quanto più piccola possibile. Per far si che la vε sia quanto più piccola
possibile bisogna accrescere tm,max, (cioè il tempo massimo che possiamo tollerare prima che il
sistema dia luogo ad un errore di sincronizzazione), oppure bisogna cercare di ridurre τ. In tal modo
quando più è piccola questa fascia d’incertezza (di ampiezza 2vε) tanto meno probabile è che si
abbia un errore di sincronizzazione. Consideriamo che il segnale va abbia delle transizioni con
uguali tempi di salita e di discesa, come mostrato in figura 3.45; supponiamo, inoltre, che tale
segnale effettui le transizioni con una propria frequenza media di commutazione.
Sistemi sequenziali
199
Fig. 3.45 - Possibile andamento di va (con tr=tf)
Alla fascia di tensione critica di ampiezza 2vε corrisponderanno degli intervalli di tempo critici, di
ampiezza tε se il clock cambia proprio durante questi intervalli di tempo si ha un errore di
sincronizzazione. Ipotizzando che il segnale vari linearmente si ha che l’ampiezza di questi
intervalli è data da:
tε = tr
2v ε
VDD
In realtà, per ogni periodo (Tsignal) del segnale asincrono a, abbiamo due possibili commutazioni,
Pε =
2t ε
Tsignal
ovvero due degli intervalli di ampiezza tε (uno per il fronte di salita ed uno per quello di discesa).
La percentuale di tempo rispetto al periodo del segnale in cui possiamo avere degli errori di
sincronizzazione è allora data da:
Questa rappresenta una sorta di probabilità d’errore, in quanto ci indica il periodo di tempo
(relativamente breve) in cui possiamo trovarci nella fascia 2vε. Però, in effetti, il segnale viene
campionato utilizzando il segnale di clock; quindi il numero di errori di sincronizzazione al secondo
è dato da:
⎡ numero di errori ⎤
N=⎢
⎥⎦ = Pε ⋅ f ck
sec
⎣
Il fattore 1/N prende il nome di MTBF, ovvero è il tempo medio fra due errori di sincronizzazione
(Mean Time Between Failures), ed è un parametro che definisce la bontà del nostro sistema. In
definitiva risulta:
Capitolo 3
200
t m, max
1
1
MTBF = =
=
N Pε ⋅ f ck
t m, max
τ
1
1
e
e τ
=
=
=
2t ε
tr
f ck ⋅ f signal 2t r f ck ⋅ f signal t 0
f ck ⋅ f signal 4v ε
f ck ⋅
VDD
Tsignal
Osserviamo che nell’espressione ottenuta, valida in generale, la costante t0 risulta essere pari a 2tr
per le ipotesi in cui ci siamo posti, ovvero clock ideale e segnale a con tr=tf finiti (ma si poteva
ipotizzare che il segnale d’ingresso fosse ideale ed il clock avesse tr e tf finiti, oppure che entrambi i
segnali avessero dei tempi di salita e di discesa molto brevi però variabili quasi in sincronia in una
certa fascia); quindi, in generale, il tempo t0 tiene conto di tutte queste non idealità.
Ovviamente a noi interessa avere un MTBF quanto più grande possibile, in modo da aumentare il
tempo medio fra due errori di sincronizzazione. L’MTBF si riduce al crescere della frequenza di
clock, dato che il segnale d’ingresso viene campionato più volte, ed ogni volta si può avere un
errore di sincronizzazione; inoltre si riduce al crescere della frequenza dei segnale d’ingresso
(infatti, se questo fosse costante non si avrebbe mai errore di sincronizzazione, dato che ad ogni
fronte del clock l’ingresso non può variare). L’MTBF può essere migliorato essenzialmente
utilizzando dei flip-flop più veloci (quindi riducendo τ) o progettando il sistema in modo tale che
tm,max, sia sufficientemente grande. Osserviamo, però, che comunque progettiamo il nostro sistema
c’è sempre una possibilità che si abbia un errore di sincronizzazione (cioè non è possibile fare in
modo che l’MTBF sia infinito); in altri termini non esiste un sincronizzatore ideale (c’è sempre una
probabilità, sebbene bassissima, che si campioni il segnale d’ingresso proprio quando esso è in
prossimità della tensione VM). L’unico parametro su cui è possibile operare è l’MTBF; rendendolo
sempre più grande si può avere una ragionevole probabilità che questo fenomeno non si manifesti in
una maniera che non è possibile tollerare.
Supponiamo, ad esempio, che si abbia una frequenza di clock fck= 100 MHz, una frequenza media
di variazione del segnale fsignal=10 MHz, un valore di t0=l ns ed una costante di tempo del flip-flop
pari a t=0.25 ns. Il valore dell’MTBF risulta allora pari a:
MTBF=10-6e 4tm,max
dove tm,max è espresso in ns. Dunque se tm,max =1 ns il nostro sistema è proprio al limite, in quanto
sappiamo che per avere un corretto funzionamento del sistema sequenziale deve risultare: T ≥ tc,max
+ts+tq; in tal caso risulta MTBF≅50µs, valore del tutto inaccettabile. Del resto se si porta tm,max a soli
5 ns si ha MTBF≅8 min., mentre per tm,max =8 ns si ha: MTBF≅60 anni. Quest’ultimo valore può
sembrare molto grande, ma è il tempo medio fra due errori di sincronizzazione per uno degli
esemplari del nostro circuito; è chiaro allora che se vengono prodotti 60x365 esemplari,
mediamente mio di questi ogni giorno ha un errore di sincronizzazione. Inoltre, questo valore può
essere grande o meno in base alla tipica applicazione (in base a ciò che può accadere quando si
manifesta un errore di sincronizzazione).
Da questo esempio si deduce che, nel progetto del nostro sistema, bisogna avere come specifica
l’MTBF; dalla relazione precedente si ricava il tm,max in base al quale progettare il sistema.
Osserviamo che deve risultare tm,max= T-ts-tq, in cui il tempo combinatoriale massimo viene
Sistemi sequenziali
201
comunque ridotto per aumentare la velocità del sistema, come anche si cercano di rendere più veloci
possibile i flip-flop (riducendo il ts, ovvero il τ). Sembrerebbe, quindi, che l’unico parametro su cui
effettivamente possiamo agire sia il periodo T, ovvero bisogna rallentare la frequenza di clock.
Questo non tanto perché nell’espressione dell’MTBF compare fck a denominatore, ma perché fck
compare in tm,max che è all’esponente. Bisognerebbe, quindi, accettare una perdita di prestazioni del
nostro sistema.
Ciò, ovviamente, non può essere accettato e quindi bisogna cercare di progettare un sincronizzatore
più efficace; ciò può essere fatto nel modo mostrato in figura 3.46.
Fig. 3.46 - Sistema sequenziale con sincronizzatore più efficace
Invece di utilizzare un solo flip-flop come sincronizzatore, che in molti casi ci costringe a ridurre la
frequenza del clock per soddisfare la specifica sull’MTBF, viene utilizzato un sincronizzatore più
efficiente costituito da due flip-flop in cascata (ovvero un registro a scorrimento composto da due
flip-flop). Tale circuito è migliore del precedente, seppure abbia la limitazione di avere una latenza
maggiore (dopo due colpi di clock ci si accorge della variazione del segnale a), perché non è altro
che una versione molto semplificata del sistema sequenziale precedente, in cui c’era il flip-flop
sincronizzatore, il sistema combinatorio, che in questo caso è un filo di collegamento, ed un
registro. Quindi possiamo riapplicare la formula relativa a tm,max in cui tc,max è uguale a zero, ovvero
risulta:
tm,max= T-ts ≅ T
In pratica viene dato al primo flip-flop tutto un periodo di clock per risolvere l’uscita; appena
l’uscita viene risolta il secondo flip-flop fornisce il valore giusto, senza far vedere al resto del
202
Capitolo 3
sistema che il primo flip-flop per un certo periodo di tempo ha dato un’uscita metastabile. Questa
soluzione, nel 95 % dei casi, risolvere i nostri problemi.
Qualora, anche con questa soluzione, non fosse ancora possibile ottenere l’MTBF voluto, l’unica
soluzione è quella di aumentare la lunghezza di questo registro a scorrimento. In questo caso,
infatti, con elevata probabilità si riesce a risolvere la metastabilità del primo flip-flop; qualora
questo non accada, l’uscita del secondo flip-flop diventa metastabile. Se però utilizziamo un terzo
flip-flop, diamo anche al secondo registro un tempo T per poter risolvere l’uscita. Ovviamente si
avrà una certa cura nel progetto di questi flip-flop per cercare di renderli veloci (quindi per ridurre
la costante di tempo τ).
A livello di componenti standard (quindi di porte TTL, CMOS, ecc.) esistono dei registri, fra quelli
che si possono già acquistare, che sono predisposti per questo tipo di applicazioni (cioè come
sincronizzatori), ovvero hanno una τ particolarmente ridotta.