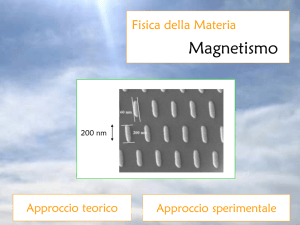
19/02/2014
SMM
Single-molecule magnets
e nanoparticelle magnetiche
Nanoparticelle magnetiche
Le nanoparticelle magnetiche hanno grande interesse per le tecnologie che
riguardano le memorie magnetiche. Ma sono anche estremamente
interessanti perché variandone le dimensioni si può studiare la transizione
dalle proprietà classiche alle proprietà quantistiche.
Comportamento
Quantistico
Atomi e
Molecole
<10-9 m
paramagnete
Comportamento
Misto
Nanostrutture
10-9 -10-7 m
Comportamento Classico
Microstrutture Oggetti Quotidiani
10-7-10-3 m
superparamagnete/
magnete
>10-3 m
magnete
1
19/02/2014
Materiali magnetici con struttura
a dominii e a singolo dominio
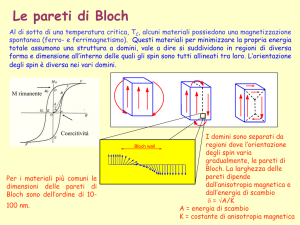
• Al di sotto di una temperatura critica, TC, alcuni
materiali possiedono una magnetizzazione spontanea
(ferro- e ferrimagnetismo).
• Per dimensioni tipicamente oltre il micron i materiali
magnetici per minimizzare la propria energia totale
assumono una struttura a domini, vale a dire si
suddividono in regioni nelle quali gli spin sono tutti
allineati tra loro. I vari domini hanno diversa forma e
dimensione, come diversa è l’orientazione della
magnetizzazione.
• I domini sono separati da regioni dove l’orientazione
degli spin varia gradualmente, le pareti di Bloch.
Pareti di Bloch (Bloch walls)
• La larghezza delle pareti dipende dall’anisotropia
magnetica e dall’energia di scambio
= A/K
• A = energia di scambio
K = costante di anisotropia magnetica
• Per i materiali più comuni le dimensioni delle pareti di
Bloch sono dell’ordine di 10-100 nm.
Bloch wall
2
19/02/2014
Anisotropia magnetica e “easy axis”
Un materiale magnetico è magneticamente anisotropo se la sua energia
interna dipende dalla direzione della sua magnetizzazione spontanea
rispetto agli assi cristallografici.
c
a
E1
Magnetizzazione lungo c
E2
Magnetizzazione lungo a
Se E1< E2 l’asse c è detto asse facile (easy axis).
L’energia di anisotropia cristallina è il lavoro che si dovrebbe fare in questo
caso per orientare la magnetizzazione (inizialmente lungo c, easy axis) lungo a
(hard axis).
L’ anisotropia magnetica è un prerequisito per la presenza di isteresi in
ferromagneti: senza di essa, un ferromagnete è superparamagnetico.
Superparamagnetismo
In nanoparticelle superparamagnetiche sufficientemente piccole c’è
solo un dominio; in tale dominio la magnetizzazione può cambiare
direzione in maniera spontanea (per effetto della temperatura). Il
tempo medio tra due successive riorientazioni del vettore è chiamato
tempo di rilassamento di Néel. Se questo tempo è piccolo, durante una
misurazione della magnetizzazione (a campo zero), il valore medio nel
tempo sarà nullo.
Per nanoparticelle in stato superparamagnetico, un campo magnetico
esterno è in grado di ottenere un valore della magnetizzazione simile
a quello di un paramagnete. Tuttavia, la suscettibilità magnetica è
molto più grande di quella tipica dei paramagneti.
3
19/02/2014
L’anisotropia magnetica deriva dalle interazioni dei momenti magnetici nella
struttura cristallina del materiale; è coinvolto l’accoppiamento S-O.
Una particella magnetica con anisotropia uniassiale ha un singolo easy axis.
Se è l’angolo tra l’asse easy e la magnetizzazione, l’energia è funzione di
tramite la
M
K anisotropy constant,
E
Energy
E KV sin 2
M’
V volume
Direzioni opposte
ma energeticamente
equivalenti
Una particella magnetica con anisotropia triassiale ha ancora un unico asse
facile, ma ha anche un asse duro (hard axis, direzione di massima energia)
e un asse intermedio (direzione associato ad un punto di sella
nell'energia).
Nanoparticelle magnetiche
Particelle a Singolo Dominio 1
La larghezza delle pareti dipende
dall’anisotropia magnetica e
dall’energia di scambio
=
= A/K
A = energia di scambio
K = costante di anisotropia
magnetica
100 nm
Quando il diametro d < la formazione di domini non è più
energeticamente favorita; tutti gli spin sono accoppiati tra loro (E di
scambio è costante).
Tipici valori di
sono:
Fe
15 nm
Co
70 nm
Ni
55 nm
NdFeB 100 nm
d
4
19/02/2014
Particelle a Singolo Dominio 2
Si abbia una particella a singolo dominio con proprietà
magnetiche anisotrope uniassiali. La magnetizzazione
sia lungo l’asse facile z :
z
M
M
M’
Energy
z
Per invertire il verso della
magnetizzazione, raggiungendo l’altro
minimo dell’energia, dovremo ruotare M di
180°, superando quindi una barriera di
energia: infatti
2
M’
E
E KV sin
Particelle a Singolo Dominio 3
Energy
• L’inversione avviene
attraverso un moto
coerente di tutti i
momenti magnetici senza
coinvolgere l’energia di
scambio
E=kAV
• L’altezza della barriera E è
perciò proporzionale solo alla
anisotropia magnetica. Questa
scala linearmente con il volume
della particella (Ean=KV)
• Quando la E << kT la
magnetizzazione fluttua
liberamente come in un
paramagnete ma la suscettività è
quella di un ferromagnete
(superparamagnetismo)
• Se il processo di inversione di M
avviene per attivazione termica
= 0exp(E /kT)
5
19/02/2014
is the time of relaxation to equilibrium magnetization
25
=0exp(/kT)
-7
0=2x10 s;/k=62 K
log()
15
1y
5
1h
1s
-5
2.5
5.0
7.5
10.0
T(K)
Come ottenere nanoparticelle magnetiche
Ci sono due modi di ottenere una nanoparticella magnetica: il
bottom-up e il top-down.
Top-down
(MNP)
6
19/02/2014
Bottom-up
SMM =
7
19/02/2014
SMM
• Magneti a singola molecola (SMM) hanno molti vantaggi
importanti rispetto a particelle magnetiche convenzionali di scala
nanometrica composti di metalli, leghe metalliche o ossidi
metallici. Questi vantaggi comprendono dimensione uniforme,
solubilità in solventi organici e leganti periferici facilmente
alterabili.
• Le informazioni digitali sono attualmente memorizzate su hard
disk, DVD e altri dispositivi grazie a particelle magnetiche. Vi è
un grande interesse da parte della società per aumentare la
densità di immagazzinamento di informazioni, che significa
aumentare il numero di bit in una data area di disco rigido o altro
dispositivo. Per aumentare la densità di informazioni digitali in
una data area, le dimensioni delle particelle magnetiche devono
diminuire conservando una anisotropia magnetica.
[Mn12O12(CH3COO)16(H2O)4].2CH3COOH.4H20
Il primo magnete a singola molecola (SMM)
M12
Mn(III)
Mn(IV)
Oxygen
Carbon
S=10
8
19/02/2014
Mn(IV)
Mn(III)
5E g
4A2g
Mn 3+
4.9 X mB
Mn4+
m eff 3.8 X mB
m eff
5E g
4A2g
S
1/2
Mn 3+
m eff 4.9 X mB
S(MnIII) = 2
Mn4+
m eff 3.8 X mB
S(MnIV) = 3/2
meff/
mB
1.732
1
2.828
3/2
3.873
2
4.899
5/2
5.91
3
6.928
9
19/02/2014
1
2
8
1
S(MnIV) = 3/2
2
3
4
7
S(MnIII) = 2
3
4
6
5
Stot(MnIII) = S1(MnIII) + S2(MnIII) + S3(MnIII) +S4(MnIII) +
S5(MnIII) + S6(MnIII)+ S7(MnIII) +S8(MnIII)=
=16, 16-1, ...0
Stot(MnIV) = S1(MnIV) + S2(MnIV) + S3(MnIV) +S4(MnIV)=
=6, 6-1, ….0
1
2
8
1
2
3
4
7
3
4
6
5
Lo stato a più bassa energia di questo SMM corrisponde
all’accoppiamento FM tra gli otto ioni Mn(III) con Stot(MnIII) = 16, e
all’accoppiamento FM tra i quattro ioni Mn(IV) con Stot(MnIV) = 6.
Lo stato a più bassa energia di questo SMM ferrimagnetico corrisponde
all’accoppiamento AF tra Stot(MnIII) = 16 e Stot(MnIV)=6
STOT (SMM) = 16 - 6 = 10
10
19/02/2014
Z
(Easy axis)
Un sistema di questo tipo è caratterizzato da anisotropia magnetica
lungo l'asse facile, il che significa che la magnetizzazione è
preferenzialmente orientato parallelamente all'asse z.
Spin Hamiltonian and energies of
Mn12
1
H H ZFS H Zeeman D( S z2 S ( S 1)) gm B BS z
3
D<0
S 10
S ( S 1) 110
E M s D( M S2 110 / 3) gm B BM S
MS = 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
11
19/02/2014
Energie dei livelli in assenza di campo magnetico esterno
E
D<0
E
EM s D( M S2 110 / 3)
a. Gli stati con MS positivi sono messi
in grafico in una buca di potenziale, e
quelli con MS negativo
in un'altra. Questo formalismo è
un'estensione di quella comunemente
utilizzato per superparamagneti.
B//Z
In campo nullo ogni coppia di livelli
MS sono degeneri. I due pozzi sono
ugualmente popolati.
b. L'applicazione di un campo magnetico lungo l'asse Z aggiunge
una interazione Zeeman al sistema, per cui le coppie di livelli Ms
non sono più degeri. Il campo magnetico applicato aumenta la
popolazione della buca di destra. Se B è grande e T è basso, la
MS = -10 stato è l'unico popolato, e la magnetizzazione raggiunge
il valore di saturazione.
12
19/02/2014
SMM unmagnetized
SMM magnetized at the
saturation value.
When the field is removed the system
must go back to thermal equilibrium
(spin relaxation). This means that at
the equilibrium half of the molecules
must be in the MS=+10 and half in the
MS=-10 state, with no resulting
magnetization. The can be monitored
by measuring the magnetization as a
function of time (M(t)).
+6
+7
+8
-6
-7
-8
+9
-9
+10
-10
At low T the spin
relaxation is very
slow
The relaxation process is made possible by the coupling of the spin
system to the environment. An important source of coupling is the spinphonon interaction, which originates from the perturbation of the crystal
field induced by lattice vibrations. The spin-phonon Hamiltonian contains
terms that connect MS to MS1. In particular, by coupling to vibrations
(phonon coupling) a given molecule can change its state from
M S M S 1
by absorbing one quantum which corresponds to the difference in energy
E(9) - E(10). The process can be going up the stairs until MS= 0 is
reached. From this state the spin can lose its energy by emitting
phonons, that is, exciting vibrational modes of the lattice, to reach the
MS=+10 state, or to return to the MS=-10 state.
13
19/02/2014
Ritorno all’equilibrio mediante
meccanismo di tunneling
H=0
M=10
M=-10
Tunneling
14
19/02/2014
Tunneling
• Below 2 K, the relaxation time becomes independent of
temperature, suggesting a quantum tunneling mechanism.
• In zero applied magnetic field the M levels are degenerate in
pairs and resonant QTM may occur between M=10 and
• M=-10, M=9 and M=-9, etc.
• This mechanism seems to be active also at higher temperature
as suggested by the dramatic change of the relaxation time
observed by applying a weak magnetic field.
• The requisite for storing information is that the magnetization
is either up or down, but if tunneling occurs, the stored
information is lost.
Resonant Quantum Tunneling
Friedman et al. Phys. Rev. Lett. 1996, 76, 3830 Lionti
et al. Nature 1996, 383.6596
15
19/02/2014
• Twelve Mn ions coupled by superexchange through oxygen
bridges give a S = 10 spin magnetic moment that is stable at
temperatures of the order of 10 K and below.
• As shown by the double well potential strong uniaxial anisotropy
of the order of 60 K yields doubly degenerate ground states in
zero field and a set of excited levels corresponding to different
projections, ms = 10, 9;…; 0; of the total spin along the easy caxis of the crystal.
• Below the blocking temperature of 3 K, a series of steps [3–5]
are observed in the magnetization M as a function of magnetic
field Hz applied along the anisotropy axis.
Un altro Magnete a Singola Molecola:
[Fe8O2(OH)12(tacn)6]Br8.9H20
Fe3+
S=5/2
O
N
C
S=10
H
16
19/02/2014
The Ferric Wheel
[Fe10(OMe)20(CH2ClCO2)10]
Ferric Wheel
Fe6
Ferris Wheel
Fe10
Fe18
Fe12
17
19/02/2014
[Cr8F8Piv16]
Gli ioni metallici definiscono un
piano ma i leganti si alternano
sopra e sotto il piano dei metalli
Anelli con un numero dispari di
unità non permettono questa
struttura
Un ringraziamento alla prof.ssa M. Brustolon per
avermi fornito il materiale relativo al Corso di
magnetochimica dell’anno scorso, dal quale ho attinto
molte delle cose che ho presentato quest’ anno
18