Mathesis Roma -17-02-2016
1.
Proposta di soluzione di Adriana Lanza
(OLIMPIADI della FISICA 1991)
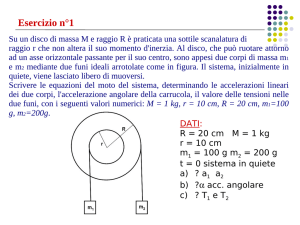
Due fili conduttori, rettilinei e paralleli, sono connessi attraverso una resistenza R. Il piano dei fili è
orizzontale e la distanza tra questi è d.
Una sbarretta di materiale conduttore , avente massa m, è appoggiata sui due fili e può muoversi senza
attrito scorrendo sempre perpendicolarmente a questi. La sbarretta è legata nel suo punto medio ad un
peso di massa
con un cavetto inestensibile e di massa trascurabile che passa su di una puleggia
(v. figura) ; anche il momento di inerzia della puleggia può essere trascurato.
E’ presente infine un campo di induzione magnetica uniforme e verticale.
Inizialmente la sbarretta è tenuta ferma; ad un certo istante viene lasciata libera, con velocità nulla.
a) Determinare , in funzione della velocità, l’accelerazione della sbarretta e la tensione del
cavetto.
b) Nell’ipotesi che i fili siano sufficientemente lunghi, determinare la velocità massima raggiunta
dalla sbarretta e l’intensità della corrente elettrica che fluisce nella resistenza, quando la
velocità della sbarretta è massima
c) Raggiunta la condizione di moto uniforme, il cavetto che tiene il peso viene tagliato e
contemporaneamente viene attivato- in serie con la resistenza R- un generatore che mantiene
la corrente al valore di regime , finché la sbarretta si ferma.
Determinare l’energia che il generatore deve erogare per frenare la sbarretta.
SOLUZIONE
a) La forza elettromotrice indotta
(cinetica)
Sollecitata dalla forza peso della massa m0 , la sbarretta acquista una velocità di modulo
destra.
Gli elettroni di conduzione della barretta , in moto e in presenza del campo
magnetico, sono soggetti alla forza di Lorentz, di modulo
,
e si sposteranno verso un estremo, mentre nell’altro estremo comparirà
una carica positiva , come in figura a lato .
Un campo elettrico, all’interno del conduttore, di intensità
si oppone alla
separazione delle cariche e compie lavoro per unità di carica pari a
,
essendo la lunghezza della barretta.
Pertanto si genera, fra l’estremo positivo e l’estremo negativo della
diretta verso
Mathesis Roma -17-02-2016
Proposta di soluzione di Adriana Lanza
sbarretta, una differenza di potenziale pari a
( forza elettromotrice indotta)
Si può verificare che i risultati sono coerenti con la legge di Faraday e
con la legge di Lenz
La forza magnetica
Nel circuito circola una corrente di intensità
il cui verso è
indicato nella figura a lato.
Nella stessa figura è rappresentata la forza
sulla sbarretta, opposta alla tensione della fune.
che agisce
Sulla sbarretta agisce pertanto una forza deceleratrice di intensità
=
Il secondo Principio della Dinamica
Consideriamo come verso positivo del moto quello che va verso destra.
Detta l’accelerazione comune alla sbarretta e alla massa
, applichiamo il secondo principio della
dinamica a ciascuna delle due masse e risolviamo il sistema così impostato
b)
La velocità di regime
La sbarretta , sotto azione delle due forze , si muove con accelerazione
inizialmente uguale a
,
ovvero a quella che avrebbe acquistato in assenza di campo magnetico, e
poi decrescente,al crescere della velocità .
Quando la velocità assume un valore limite o valore di regime in corrispondenza del quale
l’accelerazione è uguale a 0, il moto diviene uniforme , la velocità non varia e di conseguenza non varia
neanche la forza elettrica.
Mathesis Roma -17-02-2016
Proposta di soluzione di Adriana Lanza
La risultante delle forze rimane pertanto nulla e il valore della velocità non può superare quello di
regime.
Il valore di
per cui l’ accelerazione è nulla
Quando
la f.e.m. indotta è
la corrente che attraversa il circuito è
Considerazioni energetiche
Raggiunta la velocità di regime , in un intervallo di tempo
si ha :
Energia dissipata
Lavoro della forza peso
=
Energia dissipata in un certo intervallo di tempo
Lavoro della forza peso
b)
Il generatore di corrente
Il generatore inserito mantiene costante il valore dell’intensità di corrente
ma non quello della velocità e della f.e.m. indotta
Infatti, a differenza del punto a, la risultante delle forze applicate alla sbarretta non è nulla ,in quanto resta
applicata la forza frenante di modulo costante
Poiché il verso della forza è opposto alla velocità il moto della sbarretta è uniformemente ritardato con
velocità iniziale di modulo
e accelerazione di modulo
Variazione temporale della velocità
Tempo di frenata
Variazione temporale della f.e.m. indotta
Forza elettromotrice generata dal generatore per mantenere costante la corrente
Mathesis Roma -17-02-2016
Proposta di soluzione di Adriana Lanza
Considerazioni energetiche
Nell’intervallo di tempo
( intervallo di frenata) la forza frenante compie un lavoro
negativo pari a
La presenza del generatore è necessaria per mantenere costante il valore di F
La corrente che circola nel circuito dissipa una quantità di energia
Pertanto ,dall’equazione del bilancio energetico
si ottiene
=
=
Allo stesso risultato si perviene per via diretta, in quanto il lavoro del generatore può essere calcolato
come
APPROFONDIMENTI
Andamento temporale della velocità della sbarretta (punto b)
Dall’equazione
si ottiene la seguente equazione differenziale
con
ovvero
dove
ha le dimensioni di un’accelerazione
ha le dimensioni dell’inverso di un tempo
ha le dimensioni di un tempo
Mathesis Roma -17-02-2016
imponendo che
Proposta di soluzione di Adriana Lanza
si trova
Passando al limite per
velocità di regime o velocità limite
Il tempo di frenata (punto c)
Supponiamo che, come ne punto c, venga rimosso il collegamento con la massa
generatore .
, senza però inserire il
L’equazione differenziale si riduce a
con
La velocità della sbarretta segue un andamento esponenziale
e
con
costante di tempo, uguale al tempo di frenata calcolato nel punto b).
ll tempo di frenata , se l’andamento della velocità fosse esponenziale, sarebbe teoricamente infinito, ma
in pratica corrisponde a circa
. Si può verificare che
Inserendo il generatore, la velocità decresce linearmente . il tempo di frenata è minore e corrisponde
proprio a (sottotangente)
Si ha però maggior dispersione di energia per effetto Joule
Esempio
Modello esponenziale
tangente nel punto
sottotangente ( lunghezza del segmento OA)
Modello lineare
Se la velocità, raggiunto il valore di regime, diminuisce linearmente, la barretta si ferma dopo
0,38 s, mentre se diminuisse esponenzialmente, si fermerebbe dopo circa 2 s.