Esercizi sulle reti elettriche in corrente alternata (parte 3)

Esercizi sulle reti elettriche in corrente alternata (parte 3)
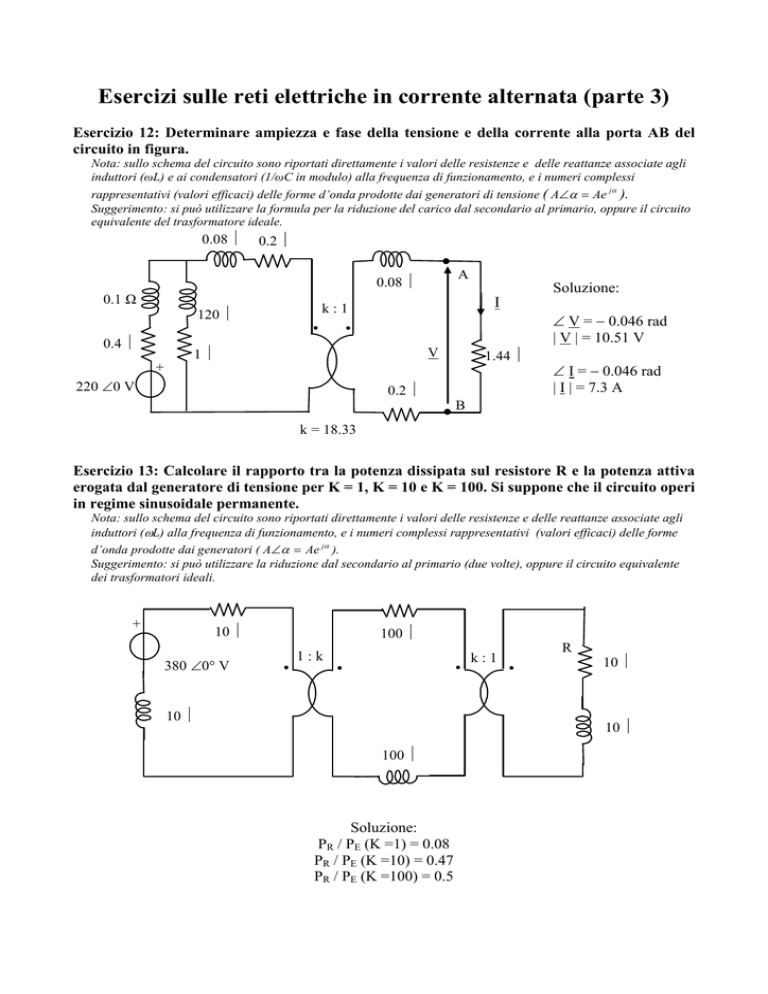
Esercizio 12: Determinare ampiezza e fase della tensione e della corrente alla porta AB del
circuito in figura.
Nota: sullo schema del circuito sono riportati direttamente i valori delle resistenze e delle reattanze associate agli
induttori (ωL) e ai condensatori (1/ωC in modulo) alla frequenza di funzionamento, e i numeri complessi
rappresentativi (valori efficaci) delle forme d’onda prodotte dai generatori di tensione ( A∠α = Ae jα ).
Suggerimento: si può utilizzare la formula per la riduzione del carico dal secondario al primario, oppure il circuito
equivalente del trasformatore ideale.
0.08 Ω
0.2 Ω
A
0.08 Ω
0.1 Ω
120 Ω
0.4 Ω
+
Soluzione:
I
k:1
∠ V = − 0.046 rad
| V | = 10.51 V
1Ω
1.44 Ω
V
220 ∠0 V
0.2 Ω
∠ I = − 0.046 rad
| I | = 7.3 A
B
k = 18.33
Esercizio 13: Calcolare il rapporto tra la potenza dissipata sul resistore R e la potenza attiva
erogata dal generatore di tensione per K = 1, K = 10 e K = 100. Si suppone che il circuito operi
in regime sinusoidale permanente.
Nota: sullo schema del circuito sono riportati direttamente i valori delle resistenze e delle reattanze associate agli
induttori (ωL) alla frequenza di funzionamento, e i numeri complessi rappresentativi (valori efficaci) delle forme
d’onda prodotte dai generatori ( A∠α = Ae jα ).
Suggerimento: si può utilizzare la riduzione dal secondario al primario (due volte), oppure il circuito equivalente
dei trasformatori ideali.
+
10 Ω
380 ∠0° V
100 Ω
1:k
k:1
10 Ω
R
10 Ω
10 Ω
100 Ω
Soluzione:
PR / PE (K =1) = 0.08
PR / PE (K =10) = 0.47
PR / PE (K =100) = 0.5
Esercizio 14: Determinare le potenze assorbite a primario dai trasformatori e verificare il
bilancio delle potenze.
Nota: sullo schema del circuito sono riportati direttamente i valori delle resistenze e delle reattanze associate agli
induttori (ωL) e ai condensatori (1/ωC in modulo) alla frequenza di funzionamento, e i numeri complessi
rappresentativi delle forme d’onda prodotte dai generatori di tensione ( A∠α = Ae jα ).
Suggerimento: si può utilizzare il circuito equivalente del trasformatore ideale.
k:1
0.02 Ω
0.08 Ω
340 Ω
T1
0.2 Ω
0.1 Ω
340 Ω
Soluzione:
+
k:1
10 ∠0 V
0.16 Ω
T2
0.4 Ω
k = 0.0545
NT1 = 29.3 + j 29.3
NT2 = 14.7 + j 14.7
Esercizio 15a: Determinare la potenza attiva Pe erogata dal generatore indipendente di
tensione e la potenza attiva PR assorbita dal resistore R del circuito in figura.
Nota: sullo schema del circuito sono riportati direttamente i valori delle resistenze e delle reattanze associate agli
induttori (ωL) e ai condensatori (1/ωC in modulo) alla frequenza di funzionamento, e i numeri complessi
rappresentativi delle forme d’onda prodotte dai generatori di tensione ( A∠α = Ae jα ).
Suggerimento: si può utilizzare la formula per la riduzione del carico dal secondario al primario, oppure il circuito
equivalente del trasformatore ideale.
2Ω
+
0.1 Ω
60 Ω
2Ω
0.1 Ω
Soluzione:
k:1
220 ∠0 V
R
2,9Ω
10 Ω
Pe = 3.92 kW
PR = 3.63 kW
k = 1.414
Esercizio 15b: Il circuito di cui sopra rappresenta il circuito equivalente di una fase di una
macchina asincrona trifase a 4 poli alimentata a 50 Hz. Valutare il rendimento η, lo
scorrimento s, la velocità di rotazione n e la coppia motrice C.
n
C
Soluzione:
η = PR / Pe = 92.7 %
s = 3.33%
n = 1450 giri/min
C = (3 PR) / ωm = 71.8 Nm