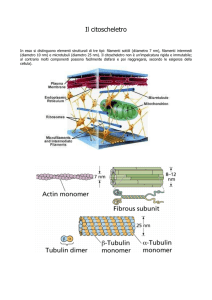
Statistica A
Ingegneria Logistica della Produzione - Teledidattico
Prova del 15 Marzo 2007
1. I fili di cotone, di diametro trascurabile, prodotti da una determinata ditta tessile possono essere
affetti da due tipi di difetti, la sfilacciatura (difetto A) e i nodi (difetto B). Il numero di difetti di tipo
A e il numero di difetti di tipo B sono variabili casuali che seguono una distribuzione di Poisson e le
due variabili casuali sono indipendenti tra loro. E' stato stimato che ogni 1000m di filo vi sono
mediamente 0.5 difetti di tipo A e ogni 10000m vi è mediamente un difetto del tipo B.
a) Calcolare la probabilità che in un rotolo di filo lungo 100.000m non vi sia alcun difetto nel tratto
tra i 60.000m e i 67.000m
b) Qual è la probabilità che in un rotolo di nastro lungo 100. 000m vi siano 3 difetti del tipo B, dato
che in esso sono stati riscontrati complessivamente 9 difetti dei due tipi?
-----------------------
0.5
, N A t~Poisson A t
1000
1
, N B t~Poisson B t
B=
10000
A=
a)
P N A 7000=0∩N B 7000=0 =P N A 7000=0 ⋅P N B 7000=0 =
−0.5
=
−1
⋅7000
e 1000
0!
⋅3.5 e 10000
⋅
0
⋅7000
⋅0.7
0!
0
−3.5
=e
−0.7
⋅e
−4.2
=e
=0.015
b)
N t =N A t N B t ~Poisson A B ⋅t , cioè Poisson
P N B 100.000=3∣N 100.000=9 =
e
=
−1
100.000
10000
3!
e
3
10 e
⋅
−0.5
100.000
10000
−0.6
100.000
10000
9!
6!
60
9
50
6
0.6
t
1000
P N B 100.000=3∩N A 100.000=6
3
P N 100.000=9
=
6
10 50
⋅
3! 6!
=0.1302
=
9
60
9!
(3pt)
© Politecnico di Torino
Data ultima revisione 04/12/08
Pagina 1 / 4
Autore: F. Pennecchi
Statistica A
Ingegneria Logistica della Produzione - Teledidattico
Prova del 15 Marzo 2007
2. Quale dovrebbe essere la numerosità del campione di batterie per cellulari da estrarre dalla
produzione della ditta produttrice se si vuole che la durata media di detto campione differisca dalla
durata media dell'intera produzione di batterie per meno del 25% della deviazione standard con una
probabilità del 98%? Si assuma che la durata delle suddette batterie segua una distribuzione normale.
-----------------------
X ~N ,
2
P ∣X −∣0.25 =0.98
P X −0.25 X 0.25 =0.98
I =0.25
=0.02⇒ 1− =0.99
2
⋅z
⇒ ṅ=
2
1−
2
I
2
⋅2.33
=
=86.86 ⇒ n87
0.25
(3pt)
3. Un prigioniero è rinchiuso in una cella con 3 porte, di qui in poi denominate con A, B e C. La porta
A si apre su un corridoio che riconduce il prigioniero nella cella dopo due ore e mezza di cammino;
la porta B conduce ad un altro corridoio che lo riconduce nella cella dopo quattro ore di cammino ed
infine la porta C gli ridà la libertà immediatamente. Il prigioniero sceglie la porta da utilizzare
lanciando due dadi omogenei in questo modo:
○
se la somma dei numeri apparsi sulla facce superiori è al più uguale a 5 sceglie la porta A
○ se la somma dei numeri è almeno uguale a 10 sceglie la porta B
○ negli altri casi sceglie la porta C.
Se poi il prigioniero torna in cella, sceglie la porta tra le due non ancora provate in modo
equiprobabile. Qual è la probabilità che il prigioniero impieghi al più quattro ore per riacquistare
la libertà?
----------------------B
6.5 h
A 1/2
C
2.5 h
1/2
A
6.5 h
B 1/2
C
4h
1/2
P (A)
P (B)
P (C)
C
P A=
0h
[
1 ,1
2, 1
3, 1
S=
4, 1
5, 1
6, 1
1 , 2
2 , 2
3 , 2
4 , 2
5 , 2
6 , 2
1 , 3
2 ,3
3 , 3
4 ,3
5 , 3
6 , 3
1,4
2 , 4
3, 4
4,4
5, 4
6,
4
1 ,5
2 ,5
3,5
4,5
5,5
6,5
1 ,6
2,6
3 ,6
4 , 6
5 , 6
6 , 6
]
10 6
16 20
; P B= ; P C =1− =
36
36
36 36
P ' tempo≤4h ' =P ' 0h ' P ' 2.5h ' P ' 4h ' =
20 10 1 6 1 7
⋅ ⋅ =
36 36 2 36 2 9
(4pt)
© Politecnico di Torino
Data ultima revisione 04/12/08
Pagina 2 / 4
Autore: F. Pennecchi
Statistica A
Ingegneria Logistica della Produzione - Teledidattico
Prova del 15 Marzo 2007
4. Il diametro (in mm) di un certo tipo di valvole è approssimativamente distribuito secondo una
distribuzione normale con media 65; si è valutato inoltre che l'84% delle valvole ha un diametro
superiore a 59.5.
1. Determinare la percentuale di valvole il cui diametro differisce dal diametro medio per più di
una volta e mezzo la deviazione standard;
2. calcolare la percentuale di valvole con un diametro superiore a 68 tra quelle con diametro
superiore alla media più metà deviazione standard
----------------------X ~ N 65, 2 ; P X 59.5=0.84 ⇒ P X 59.5=0.16
59.5−65
−5.5
5.5
⇒ P Z
=0.16 ⇒
=z 0.16 ⇒
=− z 0.16= z 0.84=0.9944
1)
2)
⇒ =
5.5
=5.53
0.9944
P ∣X −∣1.5 = P ∣Z∣1.5 = 2 P Z −1.5 =2 [ 1− P Z 1.5 ]=0.1336 ⇒ 13.36 %
P X 68∩ X 67.765
= P X 68∣X 67.765 =
=
P X 68∣X
2
P X 67.765
P X 68
1− P Z 0.54
=
=
=95.49 %
P X 67.765
1−P Z 0.5
5. Usando i dati dell'esercizio precedente, rispondere ai seguenti quesiti:
1. avendo acquistato 12 valvole di quel tipo, calcolare la probabilità che il loro diametro
medio sia compreso tra 63.5 e 66.5;
2. avendo acquistato 12 valvole di quel tipo, calcolare la probabilità che almeno 2 abbiano
un diametro compreso tra 63.5 e 66.5.
-----------------------
1) X ~ N 65, 5.532 ⇒ X ~ N 65, 5.53
12
P 63.5 X 1266.5= P
12
2
63.5−65
66.5−65
=
Z
2.548
2.548
= P −0.94Z 0.94=−1 2PZ 0.94=−12⋅0.8264=0.6528
2) Y ~Binom 12, P 63.5 X 66.5
P 63. 5 X 66.5= P
63.5−65
66.5−65
= P−0.27Z 0.27=1−2⋅0.6064=0.2128
Z
5.53
5.53
P Y ≥ 2=1 – [ P Y =0 PY =1 ]=1 –
=1−0.0566−0.1837=0.7597
[
]
12 1−0.2128 12 12 0.2128 1−0.212811 =
0
1
(4pt)
© Politecnico di Torino
Data ultima revisione 04/12/08
Pagina 3 / 4
Autore: F. Pennecchi
Statistica A
Ingegneria Logistica della Produzione - Teledidattico
Prova del 15 Marzo 2007
6. Siano X1 e X2 variabili casuali indipendenti e normali standardizzate. Si ponga Y1 = 1 + 2X1 + X2 e
Y2 = 1 + X1 - 2 X2 . Calcolare varianza e covarianza di Y1 e Y2.
-----------------------
X 1~N 0,1
}i.i.d.
X 2~N 0,1
V Y 1=4 V X 1V X 2 =41=5
V Y 2 =V X 14 V X 2=14=5
Cov Y 1, Y 2 =Cov 2X 1, X 1 Cov 2X 1, −2X 2Cov X 2, X 1Cov X 2,−2X 2 =
=2 Cov X 1, X 1 – 2Cov X 2, X 2 =2 V X 1 – 2V X 2=2−2=0
(4pt)
7. Due eventi si dicono indipendenti se
(1pt)
8. Definizione delle probabilità classica (o a propri)
(1pt)
© Politecnico di Torino
Data ultima revisione 04/12/08
Pagina 4 / 4
Autore: F. Pennecchi