Università degli Studi di Enna “Kore”
Facoltà di Ingegneria ed Architettura
Anno Accademico 2015 – 2016
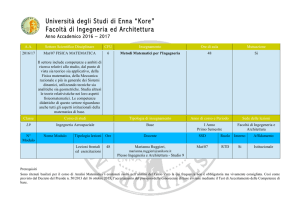
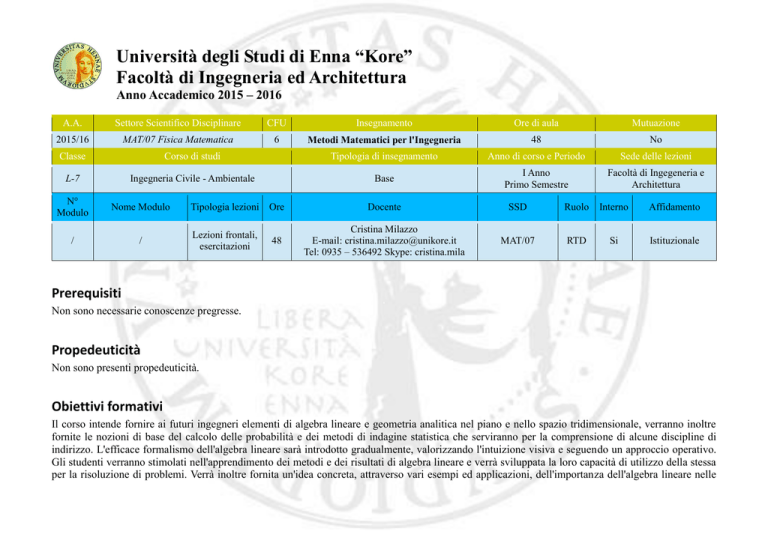
A.A.
Settore Scientifico Disciplinare
CFU
Insegnamento
Ore di aula
Mutuazione
2015/16
MAT/07 Fisica Matematica
6
Metodi Matematici per l'Ingegneria
48
No
Classe
Corso di studi
Tipologia di insegnamento
Anno di corso e Periodo
Sede delle lezioni
L-7
Ingegneria Civile - Ambientale
Base
I Anno
Primo Semestre
Facoltà di Ingegeneria e
Architettura
N°
Modulo
Nome Modulo
/
/
Tipologia lezioni Ore
Lezioni frontali,
esercitazioni
48
Docente
SSD
Ruolo
Interno
Affidamento
Cristina Milazzo
E-mail: [email protected]
Tel: 0935 – 536492 Skype: cristina.mila
MAT/07
RTD
Si
Istituzionale
Prerequisiti
Non sono necessarie conoscenze pregresse.
Propedeuticità
Non sono presenti propedeuticità.
Obiettivi formativi
Il corso intende fornire ai futuri ingegneri elementi di algebra lineare e geometria analitica nel piano e nello spazio tridimensionale, verranno inoltre
fornite le nozioni di base del calcolo delle probabilità e dei metodi di indagine statistica che serviranno per la comprensione di alcune discipline di
indirizzo. L'efficace formalismo dell'algebra lineare sarà introdotto gradualmente, valorizzando l'intuizione visiva e seguendo un approccio operativo.
Gli studenti verranno stimolati nell'apprendimento dei metodi e dei risultati di algebra lineare e verrà sviluppata la loro capacità di utilizzo della stessa
per la risoluzione di problemi. Verrà inoltre fornita un'idea concreta, attraverso vari esempi ed applicazioni, dell'importanza dell'algebra lineare nelle
Università degli Studi di Enna “Kore”
Facoltà di Ingegneria e Architettura
applicazioni.
Università degli Studi di Enna “Kore”
Facoltà di Ingegneria e Architettura
Risultati di apprendimento (Descrittori di Dublino):
Alla fine del corso, gli studenti dovranno aver conseguito le seguenti abilità, conoscenze e competenze:
Conoscenza e capacità di comprensione: Il principale obiettivo formativo del corso consiste nell'apprendimento e nella pratica del linguaggio
matematico indispensabile per trattare e comprendere le discipline scientifiche. Lo Studente al termine del corso dovrà dimostrare conoscenza
sufficiente degli argomenti oggetto del corso stesso, l’acquisizione del linguaggio proprio della disciplina e la capacità di comprendere percorsi
ipotetico-deduttivi.
Conoscenza e capacità di comprensione applicate: L’obiettivo di questo insegnamento è, da un lato, quello di abituare lo studente ad affrontare
problemi formali, utilizzando strumenti adeguati ed un linguaggio corretto e dall’altro di risolvere problemi specifici di tipo soprattutto geometrico, con
gli strumenti classici dell’algebra lineare.
Autonomia di giudizio: Lo studente dovrà acquisire la capacità di adoperare gli strumenti matematici più idonei alla risoluzione dei problemi
affrontati.
Abilità comunicative: Lo studente dovrà acquisire la capacità di esporre in modo completo e corretto, anche linguisticamente, le conoscenze e le
tecniche acquisite.
Capacità di apprendere: Lo studente dovrà acquisire anche autonomamente mediante la consultazione di testi idonei, le conoscenze matematiche
necessarie al suo corso di studi.
Contenuti e struttura del corso
Lezioni frontali:
N. ARGOMENTO
1
2
Cenni di Strutture algebriche: Insiemistica, Relazioni binarie. Relazioni di equivalenza e d'ordine.
Operazioni binarie. Semigruppi, gruppi, anelli, corpi, campi. Teorema di unicità dell’elemento neutro.
Numeri complessi e struttura algebrica dell’insieme dei numeri complessi.
Matrici ad elementi in un campo: Somma tra matrici. Gruppo abeliano delle matrici. Prodotto di uno
scalare per una matrice. Prodotto tra matrici. Proprietà delle operazioni tra matrici. Anello delle matrici
quadrate. Matrici triangolari, diagonali e scalari. Matrici trasposte. Matrici simmetriche ed
antisimmetriche. Matrici hermitiane e normali. Determinante di una matrice quadrata e sue proprietà.
Primo e secondo teorema di Laplace. Matrici invertibili. Matrice aggiunta. Calcolo dell’inversa di una
TIPOLOGIA
DURATA
Frontale
4h
Esercitazione
2h
Frontale
3h
Università degli Studi di Enna “Kore”
Facoltà di Ingegneria e Architettura
matrice. Rango di una matrice. Matrici ridotte e metodo di riduzione. Rango delle matrici ridotte.
Teorema di Kronecker.
3
4
5
6
7
8
Sistemi di equazioni lineari: Teorema di Rouche-Capelli. Teorema di Kramer. Sistemi omogenei.
Risoluzione dei sistemi lineari. Metodo di eliminazione di Gauss.
Spazi vettoriali e loro proprietà: I vettori geometrici dello spazio ordinario. Somma di vettori. Prodotto di
un numero per un vettore. Prodotto scalare. Componenti dei vettori e operazioni mediante componenti.
Definizioni ed esempi di spazi vettoriali astratti. Sottospazi. Generatori di uno spazio. Spazi vettoriali
finitamente generati. Dipendenza e indipendenza lineare. Criterio di indipendenza lineare. Base di uno
spazio. Metodo degli scarti successivi. Completamento di un insieme libero ad una base. Lemma di
Steinitz. Dimensione di uno spazio vettoriale. Formula di Grassmann. Basi ortonormali. Procedimento di
ortonormalizzazione di Gram-Schmidt.
Applicazioni lineari fra spazi vettoriali: Definizione e proprietà delle applicazioni lineari. Il nucleo e
l’immagine di una applicazione lineare. Iniettività, suriettività, isomorfismi. Teorema del Nucleo e
dell’Immagine. Studio delle applicazioni lineari. Matrice del cambio di base. Matrici simili.
Autovalori, autovettori ed autospazi di un endomorfismo: Calcolo degli autovalori: polinomio
caratteristico. Autospazi e loro dimensione. Indipendenza degli autovettori. Endomorfismi semplici e
diagonalizzazione delle matrici.
Geometria. Sistemi di coordinate nel piano e nello spazio: Coordinate omogenee e punti impropri. Rette
reali del piano e loro equazioni. Mutua posizione tra rette. Ortogonalità e parallelismo. Il coefficiente
angolare di una retta. Fasci di rette. Distanze. I piani dello spazio ordinario. Le rette dello spazio e vari
modi di rappresentazione. Ortogonalità e parallelismo. Rette complanari e rette sghembe. Angoli fra rette
e piani.
Cenni di Coniche nel piano: Definizioni e classificazioni delle coniche. Invarianti ortogonali. Riduzione
di una conica a forma canonica. Coniche riducibili e irriducibili. Significato geometrico del rango della
matrice associata ad una conica. Classificazione delle coniche irriducibili. Studio delle coniche in forma
Esercitazione
3h
Frontale
2h
Esercitazione
2h
Frontale
4h
Esercitazione
2h
Frontale
3h
Esercitazione
1
Frontale
2h
Esercitazione
2h
Frontale
2h
Esercitazione
2h
Frontale
2h
Università degli Studi di Enna “Kore”
Facoltà di Ingegneria e Architettura
canonica. Fuochi, direttrici ed eccentricità. Iperboli equilatere. Centro ed assi di simmetria.
Circonferenze. Tangenti.
9
Cenni sulle Quadriche: Definizioni e classificazioni delle quadriche. Quadriche riducibili e irriducibili.
Vertici delle quadriche e quadriche degeneri. Classificazione affine delle quadriche. Coni e cilindri.
Invarianti ortogonali. Rette e Piani Tangenti.
10 Cenni di Calcolo delle Probabilità e Statistica: Cenni di calcolo combinatorio. Disposizioni,
Permutazioni, Combinazioni, semplici e con ripetizione. Definizione di spazio delle Probabilità.
Esercitazione
2h
Frontale
3h
Esercitazione
1h
Frontale
4h
Attività esercitative: Alcune lezioni saranno dedicate alle esercitazioni, durante le quali verranno illustrare le tecniche risolutive di alcuni semplici
problemi. In tali occasioni lo studente avrà la possibilità di acquisire e approfondire i concetti proposti durante le lezioni teoriche. Inoltre lo studente
potrà verificare il proprio grado di preparazione raggiunto fino a quel momento e avrà la possibilità di concordare delle azioni di recupero per colmare
le eventuali lacune emerse.
Testi adottati
Testi principali:
A. Carfagna, L. Piccolella “Complementi ed esercizi di Geometria e Algebra lineare”, Ed. Zanichelli (2003).
P. Maroscia “Geometria e Algebra lineare”, Ed. Zanichelli (2002).
Materiale didattico a disposizione degli studenti: Durante il corso il docente fornirà alcune dispense da utilizzare come materiale integrativo per lo
studio della disciplina.
Testi di riferimento:
R. Monaco, A. Rèpaci “Algebra lineare”, Ed. Celid “Quaderni di Matematica per le Scienze Applicate”.
Testi di approfondimento:
P. Bonacini, M.G. Cinquegrani, L. Marino, Algebra Lineare: Esercizi svolti, Ed. Cavallotto, Catania 2012
P. Bonacini, M.G. Cinquegrani, L. Marino, Geometria Analitica: Esercizi svolti, Ed. Cavallotto, Catania 2012
Università degli Studi di Enna “Kore”
Facoltà di Ingegneria e Architettura
Modalità di accertamento delle competenze
L’accertamento delle competenze avverrà attraverso una prova scritta ed una successiva prova orale (il cui accesso è vincolato al superamento della
prova scritta). Durante la prova scritta, lo studente dovrà risolvere 3 o 4 esercizi su argomenti trattati durante il corso. La prova dura indicativamente 3h
e, durante la prova, lo studente potrà utilizzare una calcolatrice non programmabile, è altresì ammesso è ammesso l’utilizzo di un formulario ma non di
libri e o appunti. I fogli per l’esecuzione della prova saranno forniti dal docente. Per la partecipazione alla prova scritta è richiesta la preventiva
prenotazione sul sito di facoltà.
Il docente, indicativamente entro 3-4 giorni dalla prova scritta, pubblicherà gli esiti della prova con l’elenco degli studenti ammessi alla prova orale. La
valutazione della prova scritta è costituita da un giudizio di idoneità che consente l’accesso alla prova orale. Come regola generale, il risultato riportato
nella prova scritta di un qualsiasi appello è valido solo per la prova orale del medesimo appello che si terrà circa dieci giorni dopo la prova scritta. Se la
prova scritta è risultata quasi sufficiente si considera la prova superata con riserva e pertanto lo studente dovrà integrare l’esame mediante lo
svolgimento di uno o più esercizi in sede di prova orale. La prova orale si basa su un colloquio sull’intero programma del corsoe ha lo scopo di
appurare il raggiungimento degli obiettivi minimi fissati per il superamento dell’esame. Il mancato superamento della prova orale determina
l'invalidazione del voto riportato nella prova scritta, che deve essere ripetuta nell’appello in cui si intende ripetere l’esame.
Orari di lezione e date di esame
Gli orari di lezione saranno pubblicati sulla pagina web del corso di laurea almeno due mesi prima dell’inizio delle lezioni:
http://www.unikore.it/index.php/attvita-didattiche-ingegneria-civile-e-ambientale/calendario-lezioni
Le date di esami saranno pubblicati sulla pagina web del corso di laurea almeno due mesi prima dell’inizio della sessione d’esami:
http://www.unikore.it/index.php/ingegneria-civile-ambientale-esami/calendario-esami
Modalità e orari di ricevimento
Gli orari di ricevimento saranno pubblicati sulla pagina personale del docente:
http://www.unikore.it/index.php/ing-civile-ambientale-persone/docenti-del-corso/itemlist/category/1558-milazzo
Note
Nessuna.