Il flusso
concatenato
Induzione magnetica
1
B è solenoidale ⇔
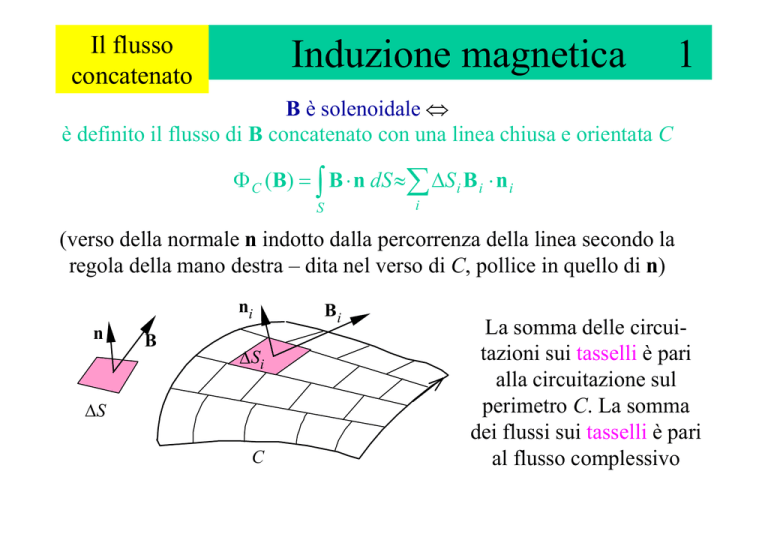
è definito il flusso di B concatenato con una linea chiusa e orientata C
Φ C (B) = ∫ B ⋅ n dS ≈∑ ∆S i B i ⋅ n i
i
S
(verso della normale n indotto dalla percorrenza della linea secondo la
regola della mano destra – dita nel verso di C, pollice in quello di n)
ni
n
B
∆Si
∆S
C
Bi
La somma delle circuitazioni sui tasselli è pari
alla circuitazione sul
perimetro C. La somma
dei flussi sui tasselli è pari
al flusso complessivo
Legge di
Faraday
Induzione magnetica
Legge di Faraday (~1830)
n
S
n
t
C
t
La circuitazione del campo elettrico E lungo
una linea chiusa C è pari alla velocità di
cambio cambiata di segno del flusso di
campo magnetico B concantenato con C.
d
∫C (E ⋅ t )dC = − d t ∫ B ⋅ n dS
S
Il flusso concatenato cambia
¾perché B cambia nel tempo
¾perché C si sposta o deforma
Derivata
totale !
2
B cambia nel
tempo
Induzione magnetica
3
∆B
∑ ∆l ⋅ E = −∑ ∆S ∆t ⋅ n
C
S
n
B
∆S
E
N
C
v
∆l
∂B
⋅ ndS
∂t
S
∫ dl ⋅ E ≡∫ (∇ × E)ndS = −∫
C
S
⇓
Forma puntuale
della legge di
Faraday
∂B
∇×E = −
∂t
C si deforma
Induzione magnetica
z
B
y
x
+
+
L
E
V
v
−
∂ Φ( B) ∆S
V=
=
B = LvB
∂t
∆t
4
Il circuito C è costituito
da una linea ad U chiusa
da una barra mobile in
moto verso destra con
velocità v, in un campo
magnetico costante B
normale al piano della
linea. Il flusso aumenta
con velocità B∆S/∆t e un
voltmetro inserito nel
circuito legge un
differenza di potenziale V
che produrrebbe una
corrente generante un
campo opposto a B.
C mobile in
B variabile
formula generale induzione 10
Formula generale della induzione su spira mobile C in B variabile
∂B
f.e.m. ≡ ∫ E ⋅ dl = ∫ (v × B ) ⋅ dl − ∫
⋅ ndS
∂t
C
C
S
d
= − Φ C (B )
dt
Legame con
la relatività
Faraday, Lorentz, Einstein 11
v
q
E
qv × B
∇×E = −
N
∂B
∂t
N
... Ma se il magnete è fermo e il
conduttore è in moto non vi è campo
elettrico in prossimità del magnete;
tuttavia nel conduttore troviamo una
forza elettromotrice [prodotta dalla
forza di Lorentz] …
v
A. Einstein Sulla elettrodinamica dei corpi in
movimento, (1905).
“L’elettrodinamica porta
ad asimmetrie che non
sembrano inerenti ai
fenomeni. ... Quando il
magnete è in moto e il
conduttore fermo, si
determina vicino al
magnete un campo elettrico
con un’energia ben definita
[per la legge di Faraday]
che produce una corrente
nei luoghi occupati dal
conduttore…
Nascita della
relatività
Faraday, Lorentz, Einstein 12
A. Einstein
Sulla elettrodinamica dei corpi in movimento, (1905):
“... Ciò suggerisce che ... le stesse leggi dell’elettrodinamica e
dell’ottica saranno valide per ogni sistema di riferimento per il
quale le equazioni della meccanica sono valide.
Innalziamo questa congettura, d’ora innanzi chiamata
‘Principio di Relatività’,
allo stato di postulato”.
Definizione
Induttanza
22
Una spira percorsa da corrente I genera un flusso di B autoconcatenato
proporzionale ad I : Φ S (B ) = LI con L = induttanza, proprietà
geometrica della spira (o circuito chiuso)
B
I
Per la legge di Faraday e spira indeformabile
dΦ S (B)
dI
f.e.m.(spira) = −
= −L
dt
dt
L ha le dimensioni di resistenza×tempo e si misura in henry (H)
1 henry = 1 Ω ×s
Energia
Induttanza
23
Lavoro per portare la corrente della induttanza da I(0)=0 a
I(t) calcolato partendo dalla espressione della potenza
elettrica W
dI
W = f.e.m ⋅ I = − L I
dt
Wdt = − LIdI
L
I (t )
1 2
lavoro = ∫ Wdt = − L ∫ IdI = − LI (t )
2
0
Come per la carica del condensatore, il lavoro è negativo
perché compiuto sull’induttanza e non fatto
spontaneamente dal campo
La densità di
energia
N
B = µ0 I
l
B
Induttanza del solenoide 24
Φ(B) = NBπ r 2 = µ 0
πr2
0....
N
I
l
En( I ) =
π r2 N 2
1 2
πr N I
1
LI = µ 0
=
2
2l
2µ 0
2
2 2
l
I
Il flusso autoconcatenato
di B è dato dal numero N
delle spire per il flusso
attraverso la sezione πr2
πr2N 2
Φ (B )
L=
= µ0
I
l
2
N
1
2
=
I
r
l
B 2 ⋅ Vol
µ
π
0
l
2µ 0
1
energia
=
B2
volume 2 µ 0
Per un solenoide molto lungo, l’energia di B è concentrata quasi tutta
all’interno del solenoide; la formula della densità di energia vale sempre
densità di energia =
Induttanze in serie 25
V1
V2
L1
L2
V1 = − L1
I
dI
dI
V2 = − L 2
dt
dt
serie
V = V1 + V2 =
= −(L1 + L2 )
dI
dt
⇒ L = L1 + L2
L’induttanza complessiva di due induttanze in serie (cioè percorse
dalla stessa corrente) è pari alla somma delle induttanze
Induttanze in parallelo 26
V = − L1
dI 1
dt
I1
I2
dI
V = − L2 2
dt
parallelo
d(I 1 + I 2 ) V
V
V
=−
=
+
L
dt
L1 L2
1
1
1
⇒ =
+
L L1 L2
L’induttanza complessiva di due induttanze in parallelo, cioè con
uguale differenza di potenziale, è uguale al reciproco della somma
dei reciproci delle induttanze
Circuito RL
R
Equazione della maglia;
interruttore chiuso a t=0
I
VG
L
V(t)
−VG + I ( t ) R + V ( t ) = −VG + I ( t ) R + L
dI ( t )
=0
dt
V
dI(t)
R
= − I(t) − G
R
dt
L
I(t)/I∞
0.8
R
t
−
VG
L
I (t ) =
1− e
R
0.4
0
27
0
2
4 t/(L/R)
La corrente aumenta e tende
asintoticamente al valore VG/R
che si avrebbe in assenza di L
La costante di tempo della crescita della corrente è L/R