Circuito RL
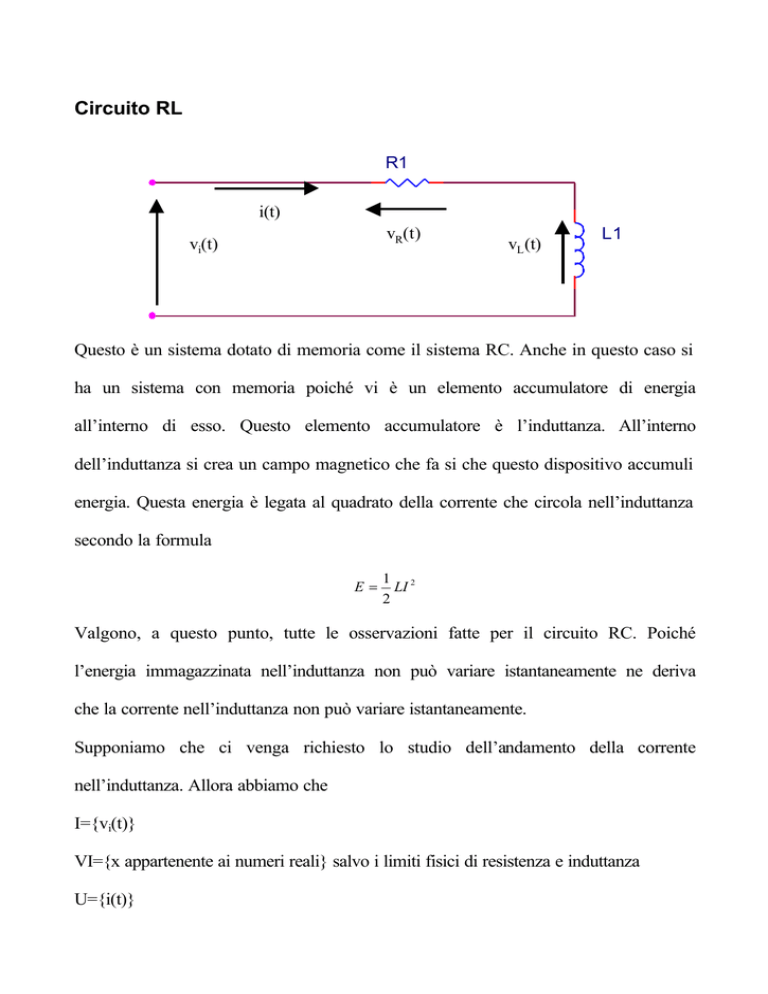
R1
i(t)
vR(t)
vi(t)
vL (t)
L1
Questo è un sistema dotato di memoria come il sistema RC. Anche in questo caso si
ha un sistema con memoria poiché vi è un elemento accumulatore di energia
all’interno di esso. Questo elemento accumulatore è l’induttanza. All’interno
dell’induttanza si crea un campo magnetico che fa si che questo dispositivo accumuli
energia. Questa energia è legata al quadrato della corrente che circola nell’induttanza
secondo la formula
E=
1 2
LI
2
Valgono, a questo punto, tutte le osservazioni fatte per il circuito RC. Poiché
l’energia immagazzinata nell’induttanza non può variare istantaneamente ne deriva
che la corrente nell’induttanza non può variare istantaneamente.
Supponiamo che ci venga richiesto lo studio dell’andamento della corrente
nell’induttanza. Allora abbiamo che
I={vi(t)}
VI={x appartenente ai numeri reali} salvo i limiti fisici di resistenza e induttanza
U={i(t)}
VU={x appartenente ai numeri reali} salvo i limiti fisici di resistenza e induttanza
Per le considerazioni energetiche viste prima abbiamo che I=S, poiché la variabile di
stato coincide con la variabile di uscita.
Determiniamo la funzione di transizione di stato usando i principi di Kirkhhoff
v i (t ) = v R (t ) + v L (t )
v i (t ) = Ri( t ) + v L ( t )
∆i
∆t
i (t ) − i ( t1 )
v i (t 2 ) = Ri( t 2 ) + L 2
∆t
v i (t ) = Ri( t ) + L
Per semplificare l’espressione dell’equazione confondiamo la corrente all’istante t2
con al corrente all’istante t1.
i (t 2 ) − i ( t1 )
∆t
v i (t 2 )∆t = Ri (t 1 ) ∆t + Li(t 2 ) − Li( t1 )
v i (t 2 ) = Ri( t1 ) + L
Li(t 2 ) = vi (t 2 ) ∆t − Ri (t1 )∆t + Li( t1 )
i (t 2 ) = vi (t 2 )
∆t R
∆t v ( t )
− i (t1 )∆t + i ( t1 ) = i ( t1 ) + i 2 − i ( t1 )
L R
L L
R
Abbiamo rimaneggiato l’equazione che descrive la funzione di trasformazione
dell’uscita in modo che appaia il fattore
L
. Questo fattore ha le dimensioni di un
R
tempo. Infatti, l’unità di misura dell’induttanza è l’henry
1henry =
per cui
volt * s
ampere
volt * s
L ampere
R = volt = s
ampere
siamo di fronte dunque ad una costante di tempo che detta la velocità con cui si
evolve l’uscita.
Ancora una volta possiamo effettuare un’analisi del sistema, bypassando le difficoltà
derivanti dal fatto che non possediamo ancora alcuni strumenti matematici, mediante
un metodo approssimato che da però uno strumento non costituito da una equazione
finita o algebrica bensì una formula che costituisce un modello iterativo.
CORRENTE NELL'INDUTTANZA
0,12
0,1
0,08
0,06
CORRENTE NELL'INDUTTANZA
0,04
0,02
0
0
0,000005
0,00001
Vedi foglio di simulazione.
0,000015
0,00002
0,000025
0,00003
0,000035