Confronti multipli

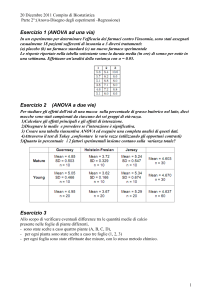
Il livello di burnout dipende dal reparto?
Strumenti di indagine
per la valutazione psicologica
Soggetto
Burnout
Reparto
1
22
Rianimaz
2
19
Rianimaz
3
23
Rianimaz
4
20
Rianimaz
5
18
Rianimaz
6
16
Ostetricia
7
12
Ostetricia
8
17
Ostetricia
9
14
Ostetricia
10
13
Ostetricia
11
12
Iperbarica
12
11
Iperbarica
13
18
Iperbarica
14
13
Iperbarica
15
15
Iperbarica
4.2 – Confronti multipli
Davide Massidda
[email protected]
Università di Cagliari, a.a. 2013/2014
H 0 : μ1 =μ 2 =μ 3
H 1 : ∃i , j∣μi ≠μ j
Risultato dell'ANOVA
●
●
Il fattore Reparto risulta statisticamente significativo
(F(2,12) = 12.30, p < 0.01, η2 = 0.67).
Possibili confronti
●
Rn ≠ Os
Rifiutiamo H0: ci sono almeno due reparti che presentano
valori medi significativamente diversi.
●
●
Quali sono le medie che differiscono fra loro? E se ci
fosse più di una differenza?
μ Rn
μ Os
μ Ip
Le ipotesi che si potrebbero fare sono tre, tutte
potenzialmente valide:
●
Rn ≠ Ip
Os ≠ Ip
A meno che il fattore non abbia solo due livelli, si
rendono necessarie ulteriori analisi (confronti multipli)
per capire qual è la “sorgente” della significatività.
Nota bene: è sempre buona prassi eseguire i confronti
multipli solo se l'ANOVA ha evidenziato una significatività
del fattore.
Approcci ai confronti multipli
Contrasti pianificati (a priori)
●
Vengono pianificati prima di eseguire l'ANOVA,
impostando delle specifiche matrici di contrasto che
saranno utilizzate per stimare i parametri del modello.
Approcci ai confronti multipli
Confronti post-hoc (a posteriori)
●
●
●
●
●
Il numero di confronti possibili è limitato dai gradi di
libertà e da alcuni vincoli da rispettare nella costruzione
delle matrici di contrasto.
●
Comunemente, vengono eseguiti a seguito di un risultato
significativo evidenziato dall'ANOVA.
Fondamentalmente, si tratta di eseguire una serie di
confronti fra le medie prese a due a due.
Ce ne sono di tanti tipi, qui ne approfondiremo tre:
I più comuni: confronti dummy, ortogonali, ortogonali
polinomiali.
1. LSD (Least Significant Difference) di Fisher
È il metodo più elegante.
3. HSD (Honestly Significant Difference) di Tukey
2. Test t con correzione di Bonferroni
Il problema dei post-hoc
●
●
●
Inflazione dell'errore di I tipo
L'uso dei post-hoc è abbastanza controverso e fra gli
statistici ci sono opinioni discordi sulle metodologie da
applicare.
H0
Vera
H0
Certo è che i post-hoc si portano dietro alcuni problemi.
Vediamo prima di tutto quali sono questi problemi, e,
successivamente, vediamo come diversi ricercatori li
hanno affrontati.
●
●
●
Non rifiuto
Rifiuto
Falsa
Errore di II tipo
Errore di I tipo
Una ricerca può trovare un risultato significativo per puro
e semplice effetto del caso (errore di I tipo).
All'aumentare del numero di test statistici che vengono
eseguiti, aumenta la probabilità di incappare in questo
problema e quindi di ottenere un p–value significativo
per effetto del caso.
Perché la probabilità di errore aumenta?
Inflazione dell'errore di I tipo
●
Se dovessimo eseguire un unico test, la domanda
sarebbe:
Inflazione dell'errore di I tipo
●
«A è diverso da B?»
●
Ma, con tre test, la domanda diventa:
«A è diverso da B e contemporaneamente A è diverso da
C e contemporaneamente B è diverso da C?»
●
L'errore di I tipo ora diventa la probabilità di rifiutare
l'ipotesi nulla quando sarebbe da accettare sia nel primo
confronto che nel secondo che nel terzo.
●
Nella prassi scientifica, la probabilità che le significatività
individuate non siano effetto del caso deve essere pari
almeno al 95%, ovvero 0.95.
H0
H1
Probabilità di rigettare
correttamente H0
A=B
A=C
B=C
A≠B
A≠C
B≠C
0.95
0.95
0.95
Probabilità di rigettare correttamente tutte e tre le
ipotesi:
0.95⋅0.95⋅0.95=0.8574
Inflazione dell'errore di I tipo
●
●
Dato che 0.8574 < 0.95, c'è qualcosa che non va.
Ora, se 0.95 è la probabilità che il rifiuto di H0 non sia
dovuto a un errore, la probabilità che invece un risultato
emerga come significativo per effetto del caso (errore di I
tipo) sarà:
α=1−0.95=0.05
●
Inflazione dell'errore di I tipo
Eseguendo un numero n di test, questa probabilità
diventa:
α=1−0.95
n
Come i ricercatori hanno affrontato questo problema?
Il metodo LSD di Fisher
●
●
●
Si tratta del primo metodo di confronto multiplo,
sviluppato dallo stesso inventore dell'ANOVA.
Il metodo LSD di Fisher
●
Consiste nel calcolare una differenza minima (LSD) che
deve essere oltrepassata perché una differenza tra
medie possa essere considerata significativa.
√
LSD=t MS Error (
Date le tre differenze tra medie (in valore assoluto)
dell'esempio del burnout:
●
̄ ̄x ∣
Δ 1=∣̄x Rn−
Os
̄̄
Δ 2=∣̄x Rn−
x Ip∣
̄ ̄x ∣
Δ 3=∣̄x Os −
Ip
possiamo calcolare una soglia che, se superata, sancirà la
significatività del confronto.
Il metodo LSD di Fisher
●
Si noti che, se ni = nj (com'è tra l'altro nell'esempio del
burnout), la formula può essere semplificata:
√
LSD=t MS Error
2
n
Dati due gruppi i e j, la differenza minima richiesta perché
lo scarto tra le loro medie possa essere considerato
significativo è data da:
1 1
+ )
ni n j
Dove t è il valore critico della distribuzione t di Student
per α/2 (il test è bidirezionale), solitamente 0.05/2 =
0.025, con g.d.l. pari ai g.d.l. della varianza d'errore come
da analisi della varianza.
La distribuzione t di Student
●
●
●
La distribuzione t di Student è simile alla normale, tanto
simile che, per n > 30, le due diventano praticamente
indistinguibili (la differenza, quindi, è sostanziale solo per
piccoli campioni).
Ha un unico parametro: i gradi di libertà ν.
È la distribuzione di riferimento per il test di confronto
tra due medie.
La distribuzione t di Student
Il metodo LSD di Fisher
●
ν=3
●
ν=2
ν=1
Si può utilizzare anche un approccio un po' diverso (ma
complementare).
Invece di calcolare una soglia LSD, per ogni confronto si
esegue un test t utilizzando un denominatore comune
per tutti i confronti.
t=
●
Quale esito dovremmo aspettarci? È sempre una buona
idea guardare i dati prima di analizzarli (e non il
contrario).
√
1 1
MS Error ( + )
ni n j
Vogliamo provare con i nostri dati?
Prima di partire
●
x̄ i− x̄ j
Confronti multipli con LSD
●
Rianimazione vs Ostetricia
H 0 : μ Rn=μ Os
H 1 : μ Rn≠μOs
t=4.07
-4.07
df =12
p=0.0016
→ Rifiuto H0
+4.07
Confronti multipli con LSD
●
Rianimazione vs Iperbarica
Confronti multipli con LSD
●
H 0 : μ Rn =μ Ip
H 0 :μOs =μ Ip
H 1 :μ Rn≠μ Ip
H 1 :μ Os≠μ Ip
t =4.48
-4.48
p=0.0008
-0.41
+0.41
t =0.41
+4.48
df =12
df =12
p=0.6912
→ Rifiuto H0
Tabella riassuntiva
●
Ostetricia vs Iperbarica
Diff
LSD
t(12) p value
Rn vs Os
6.0
3.21
4.07
0.0016
Rn vs Ip
6.6
3.21
4.48
0.0008
Os vs Ip
0.6
3.21
0.41
0.6912
Si osserva una differenza significativa tra rianimazione e
ostetricia (t(12) = 4.07, p < 0.01) e tra rianimazione e
camera iperbarica (t(12) = 4.48, p < 0.001), mentre non si
riscontra alcuna differenza tra ostetrica e camera
iperbarica (t(12) = 0.41, p = 0.69).
→ Non rifiuto H0
I problemi del metodo LSD
Cosa fa il metodo LSD per contrastare l'errore di I tipo?
●
●
●
●
Il metodo LSD “protetto” prevede di effettuare confronti
solo se il risultato del test ANOVA è significativo.
Ciò che è “buona prassi” per gli altri post-hoc, per LSD
diventa una condizione imprescindibile.
La logica è che, se il valore F è significativo, allora il
rischio di incappare in un errore di I tipo è più bassa del
normale, perché sappiamo già che H0 non è valida.
Questa logica è molto controversa. Oggi, il metodo LSD è
ormai poco utilizzato.
La correzione di Bonferroni
α=0.05
α adjusted = α
nc
●
0.05
α adjusted =
=0.0167
3
●
●
La correzione di Bonferroni
Dove nc è il numero di confronti da eseguire.
●
●
Risultati dei confronti
t(12) p value
Rn vs Os
6.0
3.21
4.07
0.0016
Rn vs Ip
6.6
3.21
4.48
0.0008
Os vs Ip
0.6
3.21
0.41
0.6912
Anche con una soglia più bassa, comunque i primi due
confronti restano significativi.
Il prodotto tra p e nc viene chiamato padjusted.
Le conseguenze di Bonferroni
●
●
α adjusted =0.0167
●
Ma se moltiplico entrambi i membri per nc ottengo:
p nc <α
●
LSD
Infatti, un risultato è significativo se:
p< α
nc
Ora il nostro termine di confronto per il p-value non sarà
più α bensì αadjusted e solo se p < αadjusted potrò rifiutare H0.
Diff
In alternativa, invece di correggere il valore α, possiamo
correggere il p-value: basta moltiplicare p per il numero
di confronti nc.
●
Non dobbiamo dimenticarci dell'errore di II tipo, cioè la
probabilità di non rigettare H0 quando invece sarebbe
corretto rigettarla.
La correzione di Bonferroni fa calare il valore α di
riferimento; se i confronti sono tanti, α scende troppo,
tanto da rischiare di prendere per non significativi dei
risultati che invece dovrebbero esserlo (il test perde
potenza).
Insomma... non è che questa correzione sia esagerata?
α adjusted =
0.05
=0.0014
36
Le conseguenze di Bonferroni
●
●
Se ci sono più di tre/quattro confronti da eseguire,
l'approccio di Bonferroni rischia di diventare troppo
conservativo: per proteggerci dall'errore di I tipo, rischia
di farci cadere nell'errore di II tipo.
Il metodo HSD di Tukey
●
Quando i confronti sono più di tre, ci sono metodi
migliori di correzione del p-value come per es. il False
Discovery Rate (Benjamini e Hochberg, 1995; Benjamini e
Yekutieli, 2001).
Il test HSD di Tukey è simile a quello LSD di Fisher ma
fornisce una protezione maggiore dall'errore di I tipo.
HSD=q
●
√
MS Error 1 1
( + )
2
ni n j
Dove q è il valore critico per un certo valore α della
distribuzione studentized range, che dipende dal numero
k di medie messe a confronto e dai g.d.l., che sono pari ai
g.d.l. della varianza d'errore dell'ANOVA.
La distribuzione studentized range
●
●
●
●
●
Descrive la densità di probabilità dello “studentized
range” di una variabile distribuita normalmente.
Lo “studentized range” di una variabile è la differenza tra
il valore massimo e il valore minimo diviso per la
deviazione standard.
(“Studentizzare” significa trasformare una variabile
dividendola per la stima della deviazione standard).
I valori critici per q sono riportati nella tavola C in Conte
(2010) a pag. 230.
(Le distribuzioni q e t sono strettamente legate.)
Il metodo HSD di Tukey
●
Si noti che, se ni = nj , anche in questo caso la formula può
essere semplificata:
HSD=q
√
MS Error
n
Il metodo HSD di Tukey
●
Applicazione all'esempio del burnout
Invece di calcolare una soglia HSD, per ogni confronto si
può eseguire un test statistico utilizzando un
denominatore comune per tutti i confronti, facendo
riferimento alla distribuzione q:
q=
̄x i −̄x
√
Diff
HSD q(k=3, df=12)
Rn vs Os
6.0
3.93
5.76
0.0041
Rn vs Ip
6.6
3.93
6.33
0.0020
Os vs Ip
0.6
3.93
0.58
0.9134
j
MS Error 1 1
( + )
2
ni n j
●
●
Si noti come HSD > LSD, per cui risulta più difficile
rigettare l'ipotesi nulla.
Anche i p-value sono già di base più elevati, infatti non
hanno bisogno di correzione (non abbiamo più bisogno
della correzione di Bonferroni).
Alcune considerazioni
●
●
p value
In generale, i post-hoc che utilizzano una componente
d'errore comune e che tengono in considerazione l'errore
di I tipo, come quello di Tukey, sono considerati più
potenti.
La maggior parte dei post-hoc richiede gruppi con
osservazioni indipendenti (leggi: fattori between).
Alcune considerazioni
●
Nel calcolo dei test t, piuttosto che utilizzare la varianza
residua complessiva ottenuta dall'ANOVA (formula 1), c'è
chi preferisce l'approccio classico al test t (formula 2), che
considera unicamente le varianze dei due gruppi in
questione.
t=
t=
x̄ i− x̄ j
√
̄x i −̄x
√
[1]
1 1
MS error ( + )
ni n j
2
2
j
si (ni −1)+ s j (n j −1) ni +n j
⋅
ni + n j −2
ni n j
[2]