Elettrochimica - Dipartimento di Chimica

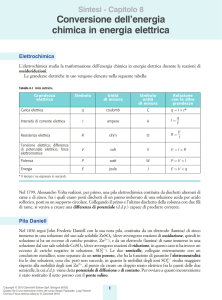
Elettrochimica
• Trasformazione di energia chimica in
energia elettrica: generatori (pile,
accumulatori, fuel cells)
• Trasformazione di energia elettrica in
energia chimica (celle di elettrolisi,
tecnologie elettrochimiche)
Sistemi Elettrochimici
• Sono costituiti da (almeno) due elettrodi
(conduttori di 1a specie o conduttori
elettronici) e da un elettrolita (conduttore
ionico o di 2a specie).
• In molte applicazioni gli elettrodi sono
metallici e l’elettrolita è una soluzione
elettrolitica.
• Quando il sistema elettrochimico è percorso
da corrente elettrica, questa è corrente
elettronica negli elettrodi e nel circuito
esterno, ed è corrente ionica nell’elettrolita.
• Nel primo caso i portatori di carica elettrica
sono gli elettroni, nel secondo sono ioni.
• Contemporaneamente, agli elettrodi
avvengono reazioni elettrochimiche.
Reazioni elettrochimiche
• Una reazione elettrochimica è una reazione
chimica nella quale compaiono gli elettroni.
• Essa deve rispettare sia il bilanciamento
delle masse che quello delle cariche
elettriche:
Cu2+ + 2e = Cu
½ O2 + 2H+ + 2e = H2O
Classificazione delle reazioni elettrochimiche
• Le reazioni elettrochimiche sono:
• di riduzione o catodiche
quando gli elettroni compaiono a primo membro
(reagenti)
2H+ +2e = H2
• di ossidazione o anodiche
quando gli elettroni compaiono a secondo
membro (prodotti)
2Cl– = ½ Cl2 + 2 e
Le reazioni elettrochimiche possono anche
essere viste come:
• reazioni di scarica ionica, se ioni reagenti si
trasformano in specie neutre
Zn2+ + 2e = Zn
2Cl– = Cl2 + 2e
• reazioni di ionizzazione, se specie neutre formano
ioni come prodotti di reazione
½ O2 + H2O + 2e = 2OH–
Na = Na+ + e
Elettrodi: catodo
• Per quanto riguarda gli elettrodi, si chiama
catodo l’elettrodo al quale avviene la
reazione di riduzione, cioè la reazione che
ha gli elettroni come reagenti.
• Questo significa che, quando il circuito è
percorso da corrente, gli elettroni entrano
nel catodo.
Anodo
• Si chiama invece anodo l’elettrodo sede
della reazione di ossidazione (reazione
anodica), cioè la reazione nella quale gli
elettroni sono prodotti.
• Quando passa corrente, gli elettroni escono
dall’anodo.
Polarità dei sistemi
• Per un elettrolizzatore (cella) il catodo è il
polo negativo del sistema e l’anodo quello
positivo.
• Al contrario, per un generatore (pila) il
catodo è il polo positivo e l’anodo quello
negativo
• In ogni caso al catodo entrano gli elettroni
che sono disponibili per la reazione di
riduzione; dall’anodo escono gli elettroni
che sono prodotti della reazione.
Continuità del circuito
• L’intensità di corrente elettrica I che attraversa il
sistema ha lo stesso valore in ogni sezione: nel
circuito esterno è dovuta al movimento di
elettroni, nel circuito interno è dovuta al
movimento di ioni (quelli positivi in un senso,
quelli negativi in senso opposto).
• Questo implica che nel circuito ionico il passaggio
di corrente sia accompagnato da un trasferimento
di materia.
Corrente elettrica e trasformazioni
chimiche
• Le reazioni elettrochimiche avvengono
all’interfaccia elettrodo/elettrolita ed eliminano la
discontinuità dei portatori di carica trasferendo la
carica elettrica dagli ioni agli elettroni.
• La superficie dell’elettrodo è quindi sede di
trasformazioni che comportano la formazione di
alcune specie chimiche e la scomparsa di altre.
Polarizzazione
• Si chiama polarizzazione chimica la
modificazione della natura chimica della
superficie dell’elettrodo in seguito al
passaggio di corrente.
• Si chiama polarizzazione di concentrazione
la variazione di concentrazione di specie
ioniche o non ioniche in vicinanza
dell’elettrodo, provocata dal passaggio di
corrente.
Sistema elettrochimico
Un classico esempio di sistema
elettrochimico (generatore) è la
Pila Daniell. Essa è costituita da
un elettrodo di Zn (anodo)
immerso in una soluzione che
contiene ioni Zn2+ e da un catodo
di Cu a contatto con ioni Cu2+.
Per evitare che si mescolino, le
due soluzioni sono separate da un
setto poroso.
14
The most primitive model of the boundary between the
solid and liquid phases is as an electrical double layer, which
consists of a sheet of positive charge at the surface of the
electrode and a sheet of negative charge next to it in the
solution (or vice versa).
This arrangement creates an electrical potential difference,
called the Galvani potential difference, between the bulk of
the metal electrode and the bulk of the solution.
15
ELECTRICAL DOUBLE LAYER
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
In the Helmholtz layer model of the
interface the solvated ions arrange
themselves along the surface of the
electrode but are held away from it
by their hydration spheres. The
location of the sheet of ionic
charge, which is called the outer
Helmholtz plane (OHP),
is identified as the plane running
through the solvated ions. In this
simple model, the electrical
potential changes linearly within
the layer bounded by the electrode
surface on one side and the OHP on
the other .
Helmholtz model (1879)
16
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
+
-
-
-
-
- - +
-
+
+
+
+
-
-
In a refinement of this model, ions that
have discarded their solvating molecules
and have become attached to the
electrode surface by chemical bonds are
regarded as forming the inner Helmholtz
plane (IHP). The Helmholtz layer model
ignores the disrupting effect of thermal
motion, which tends to break up and
disperse the rigid outer plane of charge.
In the Gouy-Chapman model of the
diffuse double layer, the disordering
effect of thermal motion is taken into
account in much the same way as the
Debye-Huckel model describes the ionic
atmosphere of an ion with the latter's
single central ion replaced by an infinite,
plane electrode.
Gouy-Chapman model (1914)
17
Neither the Helmholtz nor the Gouy-Chapman model is a very good representation
of the structure of the double layer. The former overemphasizes the rigidity of
the local solution; the latter underemphasizes its structure. The two are combined in
the Stern model, in which the ions closest to the electrode are constrained into a
rigid Helmholtz plane while outside that plane the ions are dispersed as in the GouyChapman model et another level of sophistication is found in the Grahame model,
which adds an inner Helmholtz plane to the Stern model.
Gouy-Chapman
Stern
18
Stern (1924) / Grahame (1947) Model
Distance from Surface
x
Diffusion layer
+
Ψζ +
+
+
+
+
+
Ψ0 Bulk Solution
- Stern Plane Shear Plane Gouy Plane
Gouy/Chapman
diffuse double layer and layer of adsorbed
charge
The potential at the interface can be analyzed by imagining the separation of
the electrode from the solution, but with the charges of the metal and the
solution frozen in position. A positive test charge at great distances from the
isolated electrode experiences a Coulomb potential that varies inversely with
distance. As the test charge approaches the electrode, which can be a metal
or membrane electrode, it enters a region where the potential varies more
slowly. This change in behaviour can be traced to the fact that the surface
charge is not point-like but is spread over an area.
20
At about 100 nm from the surface the potential
varies only slightly with distance because the
closer the point of observation is to the surface,
although the potential from a given region of
charge is stronger, a smaller area of surface is
sampled
(a) Far from the electrode, a point charge
experiences a potential arising from a
wide area but each contribution is weak.
(b) Close to the electrode, the point charge
experiences a potential arising from a
small area but each contribution is strong.
Provided the point charge is in a certain
range of values (and, specifically, where
image charge effects can be ignored) the
potential it experiences is largely
independent of distance.
21
The potential in this region is called the outer potential, y. As the test
charge is taken through the skin of electrons on the surface of the electrode,
the potential it experiences changes until the probe reaches the inner, bulk
metal environment, where the potential is called the inner potential, f. The
difference between the inner and outer potentials is called the surface
potential, c.
A similar sequence of changes of potential is observed as a positive test
charge is brought up to and through the solution surface. The potential
changes to its outer value as the charge approaches the charged medium,
then to its inner value as the
probe is taken into the bulk.
Now consider bringing the
electrode and solution back
together again but without any
change of charge distribution.
The potential difference
between points in the bulk metal
and the bulk solution is the
Galvani potential difference, Df
22
To demonstrate the relation between Df and E consider
the cell:
Pt│H2(g) │ H+(g)║M+(aq) │ M(s)
and the half-reactions
M+(aq) + e- → M(s)
H+(aq) + e- → 1/2 H2(g)
,
The Gibbs energies of these two half-reactions can be
expressed in terms of the chemical potentials, m, of all the
species. However, we must take into account the fact that the
species are present in phases with different electric potentials.
Thus, a cation in a region of positive potential has a higher
chemical potential (is chemically more active in a
thermodynamic sense) than in a region of zero potential.
23
Per definizione il potenziale elettrico è il lavoro necessario per portare una
carica da distanza infinita (bulk della soluzione) nell’interno del metallo.
La ddp invece è la variazione di lavoro da un punto all’altro.
Tuttavia essendo le soluzioni elettrolitiche più complicate rispetto al
metallo in soluzione, il potenziale elettrico non può essere considerato da
solo, così come accade anche al potenziale chimico, perché questi sistemi
sperimentano sia fenomeni chimici che fenomeni elettrici.
A questo scopo Guggenheim introdusse il concetto di potenziale
elettrochimico:
~
m  m + z  N A  e f
potenziale
chimico
potenziale elettrico
24
The contribution of an electric potential to the chemical potential
is calculated by noting that the electrical work of adding a charge
ze to a region where the potential is f is zef and therefore that the
work per mole is zFf, where F is Faraday's constant.
Because at constant temperature and pressure the maximum
electrical work can be identified with the change in Gibbs energy,
the difference in chemical potential of an ion with and without
the electrical potential present is zFf.
The chemical potential of an ion in the presence of an electric
~:
potential is called its electrochemical potential, m
~
m  m + z  F f
25
Energy Levels
The chemical behaviour of any substance is dictated by its energy levels: their energy, momentum, and density. Even the smallest system,
an atom, has an infinite number of energy levels, though only a few are occupied by electrons in its lowest energy condition. As atoms
combine to form molecules, the number of states is still infinite but the density of states is spread over a wider range of energy levels. A
large molecule is even more complex and finally bulk material has such a high density of states that there seems to be a continuum of
states at all energies. Chemistry is controlled by the exchange of electrons around the transition from filled to empty states. In
molecules, these are called the LUMO and HOMO states. In a solid they are called the conduction and valence bands. The Fermi level in
a solid metal is like the HOMO in a molecule.
Energy
E=0
Empty
States
LUMO
Filled
States
HOMO
An Atom
Vacuum
Level
Fermi
Level
A Small
Molecule
A Large
Molecule
Bulk
Material
Chemistry is controlled by the states around the filled/empty transition.
26
La caratteristica fondamentale del legame metallico è l'assenza di
localizzazione e direzionalità. Gli elettroni di valenza infatti non risultano
legati a un tipo di ione, ma al reticolo nel suo complesso. Possiamo spiegare
intuitivamente queste proprietà osservando che gli atomi di molti elementi
che formano legami metallici hanno un'energia di ionizzazione relativamente
bassa. Un valore basso dell'energia di ionizzazione significa che un atomo lega
debolmente gli elettroni di valenza. Di conseguenza, una volta formato il
solido, gli elettroni di valenza si separano facilmente dai loro atomi e danno
una distribuzione abbastanza uniforme di carica negativa. Formano in altri
termini quello che viene chiamato un "gas di elettroni".
27
Band Structure
Infinitesimal
spacing
between
filled and
empty states
Small but
non-zero
spacing
between
filled and
empty states
Valence
Band
Large
spacing
between
filled and
empty states
Band Gap
Core
Bands
Metal
Semiconductor
Insulator
28
Il fisico svizzero Felix Bloch elaborò la teoria delle bande definendo il
legame metallico sulla base di concetti fondamentali della meccanica
quantistica. Applicando l'equazione di Schrödinger ad una quantità di atomi
metallici tendente a infinito, si ottiene una successione di livelli energetici
orbitalici (approssimazione del legame forte): i livelli più bassi contengono
elettroni e sono definiti bande di valenza, quelli a energia maggiore sono
vuoti e rappresentano le bande di conduzione.
I conduttori metallici sono
caratterizzati da avere una banda di
valenza solo parzialmente riempita o
una banda di valenza in stretta
contiguità, o addirittura sovrapposta,
alla banda di conduzione: in questo
modo gli elettroni risultano
praticamente mobili e possono
facilmente passare da un livello di
energia E1 ad un livello E2, generando
una corrente elettrica per imposizione
di una differenza di potenziale o per
assorbimento di un determinato fotone
Aumentando la temperatura, aumentano i moti oscillatori
degli atomi lungo
hν (fotoelettricità)
.
l'asse del nodo cristallino: in questo modo il flusso libero di elettroni risulta
ostacolato e si spiega il perché la conduttanza elettrica diminuisca con
29
l'aumentare della temperatura.
Per ogni conduttore esiste il livello di energia di Fermi che
rappresenta la differenza di energia tra i livelli HOMO e LUMO.
Ogni metallo ha un suo livello di Fermi.
Quando due metalli vengono messi a contatto si avrà conduzione fino al
raggiungimento dell’equilibrio, che si verifica quando i livelli di Fermi dei
due conduttori si eguagliano:
  
  
0
F
0
F
α
F
livello di
riferimento
E
β
30
Two Conductors in Contact
Note that the vacuum level
shifts for the two materials.
This is because the charge
that is transferred establishes
a potential that produces the
shift in all the states of the
sample.
–+
–+
–+
–+
–+
electron flow
leads to charge separation
Contact potential difference
Fermi level the same throughout sample
31
An Ion in Solution
• ion’s electronic structure: HOMO, LUMO, HOMO-LUMO gap.
Lowest Unoccupied Molecular Orbital
HOMO-LUMO Gap
“Fermi” level
Highest Occupied Molecular Orbital
Energy levels have breadth because of intramolecular energy states (rotation,
vibration) and interactions with the solvent. The Fermi level is in quotes because
a Fermi level is actually ionly present for a metal, but the concept is useful here
so we use it loosely.
32
Metal in an Electrolyte Solution
Fermi levels
are aligned
Charge is transferred to
equilibrate Fermi levels,
producing a charge
separation and a contact
potential difference.
+–
+–
+–
33
Two Electrolyte Solutions
“Fermi” level
A charge separation
arises to align the
“Fermi” level and
produces a potential
at the interface.
+–
+–
+–
34
In termini di potenziali elettrochimici:
~
m  m - Ff
~
m   m  - Ff
all’equilibrio
~
~
m  m 
In una soluzione elettrolitica il livello di Fermi corrisponde ai
livelli energetici più alti per la specie che si riduce (banda di
conduzione), mentre nelle specie ossidate è nella banda di
valenza perché cedono elettroni.
Il livello di Fermi rappresenta la separazione
tra il potenziale in soluzione ed il potenziale
nell’elettrodo
35
m      
0
e
0
F
β
α
Ox
m~e  
Red
α
~
m
e
β
Ox
m~e  
Red
All’equilibrio
Se
un conduttore
metallico è nel
l’elettrone
in contatto
metallo
con
e
nella
unasoluzione
soluzione
elettrolitica
devono
avere lo stesso
contenente entrambe
potenziale
le specie redox di una
elettrochimico.
coppia, si considerano
livelli energetici
occupati i livelli
donatori di elettroni
(forma ridotta, Red);
mentre i livelli
energetici non
occupati possono
essere considerati i
livelli accettori di
elettroni (forma
ossidata, Ox)
36
In quest’ambito va inserito il
teorema di Gibbs (1875):
“non si può misurare il potenziale di
due fasi, ma solo la differenza che non
sarà mai puramente elettrica, ma
conterrà anche la componente chimica”
37
In condizioni di equilibrio i sistemi hanno potenziali elettrici o
elettrochimici uguali, per cui per una coppia redox in equilibrio in
soluzione:
-
Ox + ne  Re d
l’unica specie comune all’elettrodo e alla soluzione è l’elettrone.
In soluzione si può scrivere:
~
~
~
mOx + nme  mRed
38
m~  m + zF
~
~
~
mOx + nme  mRed
Ipotizzando, per semplicità, che la forma ridotta sia neutra per cui vale:
m~
Re d
 mRed + zF Red 
 m~Red  mRed
zF 0
Si ha:
mOx ( s ) + zFOx ( s ) + nme( s ) + nzFe( s )  mRed ( s )
inoltre, considerando l’equivalente in elettroni per cui z=-1 si ha:
mOx ( s ) + zFOx ( s ) + nme( s ) - nFe( s )  mRed ( s )
39
si immagina, sempre per semplicità, che la reazione redox scambi solo un
elettrone per cui n=1:
mOx ( s ) + zF Ox ( s ) + me ( s ) - F e ( s )  mRe d ( s ) 
m~e ( s )  me ( s ) + F e( s )  mRe d ( s ) - mOx ( s ) - zF Ox ( s )
Poiché esiste anche l’elettrodo, si potrà scrivere un’espressione
anche per l’elettrone all’elettrodo:
m~e( E )  me( E ) - Fe( E )
40
m~e( s )  mRed ( s ) - mOx ( s ) - zFOx ( s )
m~e( E )  me( E ) - Fe( E )
L’equilibrio tra le due fasi si avrà quando:
~
m
e( E )
~
m
e( s )
41
mRed ( s ) - mOx ( s ) - zFOx ( s )  me( E ) - Fe( E )
z 1
mRed ( s ) - mOx ( s ) - me( E )  zFOx ( s ) - F e( E )  Potenziale
F (Ox ( s )Galvani
- e( E ) )
dell’elettrone
nell’elettrodo 
Potenziale Galvani
dell’elettrodo
 e ( E ) -  Ox ( s ) 
- m Re d ( s ) + mOx ( s ) + me ( E )
F
Questa rappresenta la ddp dell’elettrone in soluzione all’equilibrio
con l’elettrone sull’elettrodo.
In altri termini è la ddp Galvani tra elettrodo e soluzione.
42
 e ( E ) -  Ox ( s ) 
- m Re d ( s ) + mOx ( s ) + me ( E )
F
μe(E) è una caratteristica del metallo
mRed  mOx   E -  s  0   s   E
I potenziali chimici μRed e μOx dipendono dalla
concentrazione (μ= μ °+RTlna)
43
mRed  mOx   E -  s  0   s   E
si ha che l’elettrodo si caricherà
negativamente rispetto alla soluzione
l’equilibrio si sposterà verso l’ossidazione
perché le specie in soluzione si ossidano
all’elettrodo caricandolo negativamente
mRed  mOx   E -  s  0   E   s
l’elettrodo si caricherà
positivamente rispetto alla
soluzione cedendo elettroni
la reazione andrà verso la riduzione
44
I segni degli elettrodi (anodo e catodo) in una pila
(processo spontaneo) vedono il catodo caricarsi
positivamente, l’anodo negativamente.
Basso potenziale→ elettrodo negativo → ossidazione
Alto potenziale → elettrodo positivo → riduzione
Vediamo la dipendenza del potenziale dalla
concentrazione
45
 e ( E ) -  Ox ( s ) 

- m Re d ( s ) + mOx ( s ) + me ( E )
F
0
- m 0Re d ( s ) + m Ox
+ me ( E )
(s)
F
Se si
ha:
m
0
Re d
RT aOX
+
ln
F
aRe d
 m Ox  m Ox - m Re d  0
0

0
0
tuttavia influisce
anche il rapporto
tra le attività
(aOx/aRed)
in modo da cambiare la ddp chimica:
mOx - mRed  0
46
Si considera il caso in cui l’elettrodo partecipa alla reazione redox:
M
z+
-
+ ze  M
il metallo M può ossidarsi (passaggio in soluzione del metallo come
Mz+)
il metallo M può ridursi (passaggio di ioni dalla soluzione al metallo)
In ogni caso all’equilibrio la somma dei potenziali elettrochimici dei
PRODOTTI e dei REAGENTI deve essere uguale:
~
m
M z+ ( s )
~
+ zm
e( M )
~
 mM  mM
47
m~M
mM
~
+
z
m
z+
e( M )  mM 
(s)
z+


+
zF

+
z
m
F


m
z+
e
(
E
)
e
(
E
)
M
(s)
M (s)
Potenziale elettrochimico
degli ioni
potenziale degli
elettroni sul metallo
La ddp chimico all’interfaccia sarà:
D   E -  s 
- m M + m M z+ + zme
zF
48
mM  mM mRed  mOx    E -  s  0   E   s
z+
La soluzione si carica positivamente,
mentre l’elettrodo si carica negativamente
acquistando elettroni (la specie si ossida
all’elettrodo).
ΦE basso →carica negativa
ΦE alto →carica positiva
49
fase 
interfase
Due fasi a contatto sono separate da
una superficie detta interfaccia.
bulk
Regione superficiale di 
Regione superficiale di 
bulk
fase 
Interfaccia ed interfase sono
completamente diverse, perchè
l’interfase rappresenta la regione tra le
due fasi in cui si osservano marcate
variazioni delle proprietà chimicofisiche rispetto ai valori del bulk.
Nel caso di fasi elettricamente
conduttrici in questa regione si ha una
differenza di carica.
Doppio strato elettrico
TIPO I: interfaccia non polarizzabile
possibilità che una carica elettrica possa passare rapidamente attraverso di essa
in entrambe le direzioni
TIPO II: interfaccia polarizzabile
comportamento come condensatore, cioè impermeabilità al trasferimento di carica
Un solido immerso in un liquido polare si carica elettricamente in superficie,
in genere la carica è negativa.
Tale carica causa la formazione di una struttura denominata “doppio strato
elettrico”. Le cariche negative superficiali attraggono gli ioni positivi solvatati
e orientano le molecole costituenti il liquido. Ioni e molecole generano quindi
un cuscinetto ordinato di cariche sulla superficie del solido, via via sempre
più diffuso verso il resto del liquido.
Stern (1924) / Grahame (1947) Model
Distance from Surface
x
Diffusion layer
+
Ψζ +
+
+
+
+
+
Ψ0 Bulk Solution
- Stern Plane Shear Plane Gouy Plane
Gouy/Chapman
diffuse double layer and layer of adsorbed
charge
Salt Addition
Distance from Surface
x
Diffusion layer
Original Curve
Ψζ
+
+
+
+
+
+
+
+
+
Ψ0 Bulk Solution
- Stern Plane Shear Plane Gouy Plane
Salt will not effect the value of Ψ0, but will effect the value of Ψζ
Salt Addition
Ψζ=0 Ψ0 -
Distance from Surface
+
+
+
+
+
+
+
+
Diffusion layer
x
Original Curve
-
+
-
-
+
-
+
Shear Plane
-
+
-
-
+
-
Gouy Plane
-
-
Bulk Solution
Stern Plane
Further salt addition can collapse the EDL.
-
Debye Length: EDL Thickness
Debye-Hückel parameter (κ) describes the decay length
 e
2
  
Ci Z i 

  r  0 kT i 1

2
Zi
e
Ci
n
εr
ε0
k
T
n
1/ 2
= electrolyte valence
= elementary charge (C)
= ion concentration (#/m3)
= number of ions
= dielectric constant of medium
= permittivity of a vacuum (F/m)
= Boltzmann constant (J/K)
= temperature (K)
κ-1 (Debye length) has units of length
il potenziale zeta ( z )
Una particella dispersa in un liquido
generalmente presenta delle cariche
elettrostatiche superficiali (per es. prodotte
durante la polverizzazione) che danno
luogo ad un campo elettrico responsabile
della distribuzione di ioni nello spazio che
circonda la particella. Questa distribuzione
comporta un aumento della
concentrazione di contro-ioni (ioni di
carica opposta a quella della particella) in
prossimità della superficie. In particolare,
lo strato di liquido ionizzato che circonda
la particella è composto di due zone: una
interna (strato stazionario, o di Stern), con
gli ioni fortemente legati alla particella
carica, ed una esterna (strato diffuso, o di
Gouy), dove le interazioni sono più
deboli. Le due zone, costituiscono un
doppio strato elettrico intorno a ciascuna
particella.
All'interno dello strato diffuso - di spessore molto maggiore rispetto allo
strato di Stern - gli ioni formano strutture metastabili: quando la particella si
muove nel liquido, gli ioni si muovono con essa, sostituendo ed essendo
sostituiti dagli ioni liberi presenti nel liquido in modo che le dimensioni del
doppio strato, determinate dal potenziale zeta rimangano costanti.
Variazione del potenziale elettrico in
In particolare, poiché la carica intrinseca sulla
funzione della distanza dalla
superficie della particella è schermata dalle
superficie della particella:
cariche dello strato stazionario, le interazioni
fra particelle
saranno
ovviamente
regolate
si può vedere
come
V diminuisca
proprio
dal potenziale
presente
alla
superficie
rapidamente
all'interno
dello
strato
di questo
strato. più
Immaginiamo
di
stazionario,
lentamentedunque
all'interno
allontanarci
dalladiffuso
superficie
particella,
dello strato
e poidelle
ancora
più
per raggiungere,
lungo
curva di potenziale
lentamente fino
ad la
annullarsi,
per
in figura,
il puntoall'infinito.
Z corrispondente alla
definizione,
frontiera fra lo strato diffuso e il liquido
libero: il potenziale definito in questo punto
prende il nome di potenziale zeta (z) e
definisce il comportamento dei sistemi
dispersi e delle sospensioni.
Importanza pratica del potenziale zeta
Quando due particelle sono così vicine che i loro doppi strati si sovrappongono,
si respingono reciprocamente con una forza elettrostatica la cui intensità
dipende dal potenziale z: se il potenziale zeta è troppo basso (tipicamente
inferiore a ±25 mV), la forza repulsiva non sarà abbastanza forte da superare
l'attrazione di van der Waals fra le particelle, e queste inizieranno ad
agglomerarsi. Quando questo accade la sospensione è instabile. Se la
sospensione è concentrata ed instabile, questi agglomerati formano reti ed i
colloidi formano una colla.
Un alto potenziale zeta
impedisce
l'agglomerazione delle
particelle e mantiene la
dispersione uniforme e
libera di scorrere. Di
conseguenza, l'obiettivo
nella maggior parte delle
formulazioni è
massimizzare il
potenziale zeta.
Il potenziale z dipende dalla densità della carica superficiale e dallo spessore del
doppio strato.
La densità della carica superficiale, a sua volta, dipende dalla concentrazione del
potenziale prodotto dagli ioni nei solventi ionici che hanno un'affinità particolare per
la superficie. In molti sistemi, lo ione H+ determina il potenziale e così il potenziale z
dipende dal pH.
Il potenziale z è positivo per bassi valori di pH e negativo per valori alti.
Il pH per cui il potenziale z è nullo definisce il punto isoelettrico (IEP = IsoElectric
Point) del colloide. Il punto isoelettrico è una proprietà della superficie della
particella ed è il valore intorno al quale si ha scarsa stabilità in quanto sono più
evidenti le forze di van der Waals.
Praticamente il
punto isoelettrico di
un colloide
rappresenta il punto
di massima
instabilità della
sospensione.
Zeta Potential – Effect of pH
ζ
+
+
+
+
+
+
+
ζ
Shear
Plane
Low pH: Not
enough OH- so
there is a excess
positive charge.
+
+
+
+
+
+
+
H+
OH-
ζ
Shear
Plane
There is a point
that there is enough
OH- and H+ to
completely balance
out the surface
charge
+
+
+
+
+
+
+
Shear
Plane
High pH: Not
enough H+ so
there is a excess
negative charge.
ζ (mV) +
Zeta Potential – Effect of pH
ζ
+
+
+
+
+
+
+
Isoelectric Point (IEP):
pH at which ζ = 0
pH
-
ζ
+
+
+
+
+
+
+
ζ
+
+
+
+
+
+
+
Electrokinetic Phenomena
• Electrophoresis
Movement of particle in a stationary fluid by an applied
electric field.
• Electroosmosis
Movement of liquid past a surface by an applied electric field
• Streaming Potential
Creation of an electric field as a liquid moves past a stationary
charged surface
• Sedimentation Potential
Creation of an electric field when a charged particle moves
relative to stationary fluid
Zeta Potential Measurements
• Electrophoresis
z determined by the rate of diffusion (electrophroretic
mobility) of a charged particle in a applied DC electric field.
• PCS
z determined by diffusion of particles as measured by photon
correlation spectroscopy (PCS) in applied field
• Acoustophoresis
z determined by the potential created by a
particle vibrating in its double layer due to an acoustic wave
• Streaming Potential
z determined by measuring the potential created as a fluid
moves past macroscopic surfaces or a porous plug
Elettroforesi: movimento di particelle colloidali cariche o polielettroliti
(proteine) in un liquido sotto l’influenza di un campo elettrico esterno.
La velocità elettroforetica ne (m/s) è la velocità durante l’elettroforesi.
La mobilità elettroforetica me (m2/Vs) è la velocità rispetto alla forza del
campo elettrico.
me >0 se la particella si muove verso il potenziale più basso (elettrodo negativo)
me <0 se la particella si muove verso il potenziale più alto ( elettrodo positivo)
+
-
Le particelle che danno
luogo a una fase dispersa
in un liquido, e la cui
carica è dovuta alla
formazione di un doppio
strato sulla superficie, se
vengono assoggettate
all’azione di un campo
elettrico presentano il
comportamento illustrato
schematicamente nella
figura.
Elettro-osmosi: movimento di un liquido attraverso un set di particelle
immobilizzate, un tampone poroso (plug), un capillare o una membrana in
risposta ad un campo elettrico applicato. E’ il risultato della forza esercitata dal
campo sulla contro-carica nel liquido all’interno dei capillari carichi, pori, etc. Gli
ioni in movimento trascinano il liquido in cui sono immersi.
La velocità elettro-osmotica neo (m/s) è la velocità uniforme del liquido lontano
dall’interfaccia carica.
Solitamente si misura la velocità del flusso di volume del liquido (m3/s)
attraverso il capillare, il setto o la membrana diviso per la forza del campo
elettrico Qeo,E (m4/Vs) o diviso per la corrente Qeo,I (m3/C).
Un concetto correlato è la contro-pressione elettro-osmotica Dpeo (Pa) che è
la differenza di pressione che si deve applicare attraverso il sistema per bloccare
il flusso di volume elettro-osmotico.
Dpeo>0 se la pressione è applicata sul lato in cui il potenziale elettrico è più alto.
Streaming Potential: Ustr (V) è la differenza di potenziale a corrente elettrica
nulla, causata dal flusso di liquido sottoposto ad un gradiente di pressione
attraverso un capillare, un tampone, un diaframma o una membrana. La differenza
è misurata attraverso il tampone oppure tra le estremità del capillare. Gli streaming
potentials sono generati dall’accumulo di cariche dovuto al flusso di contro-cariche
all’interno dei capillari o dei pori.
Streaming Current: Istr (A) è la corrente attraverso il tampone quando due
elettrodi sono fatti scaricare e cortocircuitare. La densità di corrente di scorrimento
(streaming current density) jstr (A/m2) è la corrente di scorrimento per unità di
superficie.
Sedimentation Potential: Used (V) è la differenza di potenziale sentita da
due elettrodi identici posizionati verticalmente ad una distanza L tra loro in una
sospensione in cui le particelle vengono fatte sedimentare sotto l’effetto della
gravità. Il campo elettrico generato Used/L è noto come campo di sedimentazione
Esed (V/m). Quando la sedimentazione è prodotta mediante centrifugazione il
fenomeno è detto centrifugation potential.
Electrophoresis :
The movement of a charged particle
relative to the liquid it is suspended in
under the influence of an applied electric
field.
Electroosmosis :
The movement of a liquid relative to a
stationary charged surface under the
influence of an electric field.
Streaming potential :
The electric field generated when a liquid
is forced to flow past a stationary
charged surface.
Sedimentation potential :
The electric field generated when
charged particles move relative to a
stationary liquid.
ELETTROOSMOSI
3) Elettroosmosi = Flusso di un elettrolita prodotto dalla presenza
di un campo elettrico che guida lo stato carico vicino alle pareti.
z
E
x
Core
E xz
up  m
Debye layers
STREAMING POTENTIAL
The inverse effect of electroosmosis
U
E
A flow generates an electric field
Consider a liquid electrolyte, consisting of positive and negative particles (“ions”)
in solution, such as NaCl salt dissolved in water. The interface between the
electrolyte and the container wall generally forms a double layer in equilibrium,
where a nonzero surface charge (due to chemical effects) is screened by a very thin
diffuse layer of excess ionic charge of width, the Debye screening length (typically
1-100 nm). The double layer is effectively a capacitor skin at the interface, which
has a small voltage across it, the zeta potential (typically 0.01 - 0.1 Volt), defined
as the potential of the surface minus the potential just outside the double layer.
Now consider a tangential electric field Ek applied parallel to a flat surface. The
electric field acts on ions in the diffuse part of the double layer, which drag the
fluid to produce an effective slip velocity outside the double layer.
At the interface between a glass surface and a liquid such as
water, silanol molecules (SiOH) on the glass surface react with
free hydroxyl ions (OH-) in the water, forming Si(OH)2- and
leaving the glass surface negatively charged. Free H+ ions in the
water are attracted by the negatively-charged surface and
accumulate near it. As a result, although the interiors of both the
glass and the liquid remain electrically neutral, an electrical
potential gradient arises in the vicinity of the interface. The
region containing this electrical potential gradient is the electric
double layer. Similar electrochemical reactions occur at most
liquid-solid interfaces as well as at other phase interfaces (solidgas, etc.). The electric double layer is the basis for a category of
phenomena known as electrokinetic effects.
Applicando
l’elettroosmosi attiva si
invertono le cariche e
così il terreno diventa
polo negativo mentre le
murature della casa poli
positivi.
Per cui l’acqua viene
attratta dal sottosuolo e
quindi i muri vengono
risanati dall’umidità.
Nel terreno si formano delle
correnti elettrostatiche
naturali, che unite all’acqua
ed ai sali minerali naturali
finiscono per creare una
polarità positiva.
Viceversa, in un edificio in
muratura si produce una
polarità negativa. Poiché
cariche opposte si attirano
succede che l’acqua presente
nel terreno viene attirata dai
muri delle case.
Electrokinetic phenomena in electrolytes
-
-
- -
-
- --
-
-
- - --
(a) Electro-osmosis = fluid slip over the double layer,
as an electric field pushes on the screening cloud
(b) Electrophoresis = particle motion due to electro-osmosis
La teoria dei fenomeni elettrocinetici coinvolge sia la
descrizione del doppio strato elettrico sia la
descrizione fluidodinamica del moto, ed è quindi
relativamente complicata.
Per formulare un modello che esemplifichi la
situazione è opportuno riferirsi a uno strato di liquido
di lunghezza l, contenente elettroliti, che si trova a
contatto con una superficie piana sotto l’azione di un
campo elettrico diretto parallelamente alla superficie
stessa. I singoli ioni tenderanno a muoversi
trascinando il solvente sotto l’azione di una forza
elettrica X, definita dalla relazione X=Df/l. Tale forza
è bilanciata dalla forza di attrito che si manifesta nel
liquido. Pertanto, per un moto laminare stazionario
ciascuno strato di liquido di spessore dz si muove
parallelamente alla superficie con una velocità u che
dipende da z ma si mantiene inalterata nel tempo.
Esprimendo l’eguaglianza fra la forza elettrica che agisce sul volume e quella di
attrito dovuta alle forze viscose, si ha:
d 2u
 du 
 du 
Xdz  m  
- m    m 2 dz
dz
 dz  z + dz
 dz  z
Equazione di Poisson:
dy
4
0




e
C

i Zi e
2
dz

i
2
X d y
d u
m 2
2
4 dz
dz
2
-
Z iy ( z ) e
k BT
2
m= viscosità
=densità di carica
Le condizioni al contorno riflettono i valori che il potenziale e la velocità del
fluido devono assumere nel cuore del fluido e in corrispondenza della distanza
d dalla superficie, che limita la zona nella quale il liquido è stazionario.
Pertanto si possono scrivere come segue:
y=0
u=ue
y=z
u=0
du/dz=0 per z→∞
per z=d
dove ue è il valore della velocità nel cuore del fluido.
L’integrazione dell’equazione
2
X d y
d 2u
m 2
2
4 dz
dz
è relativamente agevole e, tenendo conto delle condizioni al contorno, porta alle
seguenti relazioni:
Xz
ue 
4m
4mue
z 
X
La portata del liquido è espressa dal prodotto ueA=JV, dove A è la sezione dello
strato. Se si tiene ora conto che l’intensità del campo X è data dal rapporto fra
la differenza di potenziale e la lunghezza l del mezzo cui viene applicata, e si
impiega la relazione di Ohm per esprimere l’intensità di corrente introducendo
la conducibilità elettrica del mezzo x
Da cui:
D
I  xA
l
4mxJ V
z 
I
Fornisce una relazione lineare fra la portata del liquido e il potenziale zeta e,
unitamente alla espressione della ue gioca un ruolo importante nello studio dei
fenomeni elettrocinetici. Poiché non contiene parametri geometrici
caratteristici del sistema in esame, questa espressione offre uno strumento
per risalire direttamente al valore del potenziale zeta dai valori misurabili
di JV e I.
Tutti gli effetti elettrocinetici sono determinati da due fenomeni generici che si
hanno nel doppio strato elettrico: il flusso elettro-osmotico e la corrente elettrica
superficiale convettiva.
Per solidi non conduttori Smoluchowski elaborò una teoria valida per una qualsiasi
forma di una particella o di un poro in un solido, purchè il raggio di curvatura a
rispetti la condizione:
a >>1 → a deve essere molto più grande della lunghezza di Debye ()
12


2 2
  e zi ni 
   i 1

  rs 0 kT 


N
N= numero di specie ioniche presenti in
soluzione
ni=concentrazione dello ione i-esimo
rs=permittività relativa della soluzione
elettrolitica
0=permittività del vuoto
La condizione al contorno impone che una qualsiasi piccola sezione della superficie
curva del doppio strato sia considerata piatta ed è detta ”approssimazione del doppio
strato sottile” o “limite del a grande”.
Molte dispersioni acquose soddisfano questa condizione, eccetto il caso di particelle
molto piccole in un mezzo a bassa forza ionica.
Il flusso elettro-osmotico è il flusso di liquido lungo una qualunque sezione del doppio
strato sotto l’azione della componente tangenziale Et del campo esterno E.
Nella teoria di Smoluchowski questo campo è considerato indipendente dalla presenza
doppio strato, cioè si pensa che il doppio strato non venga distorto dalla presenza del
campo esterno.
Inoltre, poiché il doppio strato è considerato molto sottile rispetto al raggio della
particella, sia le linee idrodinamiche che quelle del campo sono considerate parallele
per grandi valori a.
Ciò comporta che a grandi distanze dalla superficie la velocità del liquido ueo è data da:
ADz
JV  ueo A 
4ml
L’elettroforesi è il fenomeno opposto all’elettro-osmosi: il liquido nel suo intero è fermo,
mentre le particelle si muovono rispetto al liquido sotto l’influenza di un campo elettrico.
Quando un campo elettrico viene applicato ad una soluzione elettrolitica, le particelle
cariche sospese nella soluzione vengono attratte verso gli elettrodi di carica opposta. Le
forze viscose che agiscono sulle particelle si oppongono a questo moto.
Quando si raggiunge l’equilibrio tra queste due forze la particelle si muovono con velocità
costante.
La velocità dipende da:
•Forza del campo elettrico o gradiente di potenziale
•Costante dielettrica del mezzo
•Viscosità del mezzo
•Potenziale zeta
La velocità di una particella viene comunemente definita come mobilità elettroforetica.
Poiché entrambi i fenomeni sono dovuti all’influenza del campo elettrico sul doppio strato,
che controlla il moto relativo del liquido e del solido, i risultati della teoria dell’elettroosmosi consentono di ottenere anche le corrispondenti formule per l’elettroforesi.
La velocità della particella rispetto al mezzo fermo è data da:
z
n

X 4m
uep
uep= velocità elettroforetica
Un modo alternativo per affrontare il problema consiste nel porre l’attenzione su una
particella carica sferica, in moto in un fluido per effetto di un campo elettrico. In
condizioni stazionarie la forza di natura elettrica che agisce sulla particella è
bilanciata dalle forze di attrito viscose, esprimibili mediante la legge di Stokes,
cosicché la particella si muove con velocità costante. Sviluppando tale analisi
Erich Armand Hückel ha ricavato la seguente espressione della mobilità:
z
v
6m
che, come si può osservare, differisce dalla precedente
per un fattore numerico uguale a 2/3. La precedente
equazione è stata derivata assumendo che la conducibilità
elettrica della particella sia uguale a quella del mezzo e
che le sue dimensioni siano piccole rispetto allo spessore
del doppio strato. Essa trova applicazioni per la
descrizione di fenomeni elettroforetici che hanno
luogo in soluzioni non acquose.
In una analisi più approfondita, D.C. Henry ha tenuto conto esplicitamente
dell’effetto della forma geometrica della particella sulla configurazione del campo
elettrico che si stabilisce attorno a essa.
Xz  r 
uep 
f 
m  d 
dove compare una funzione complicata ( f ) del rapporto r/d fra il raggio della
particella e lo spessore dello strato diffuso.
Lo streaming potential sorge quando una
soluzione elettrolitica fluisce a contatto
con una superficie stazionaria, o tra due
piatti, o attraverso un letto di fibre o di
granuli impaccato.
Si consideri un capillare di sezione circolare
con raggio a e lunghezza L, con pareti
cariche. Si impone dall’esterno una differenza
di pressione Dp tra le due estremità del
capillare, per spingere il liquido nel capillare.
Poiché il fluido vicino alle pareti trasporta un
eccesso di cariche sek, il suo movimento
produce una corrente elettrica nota come
streaming current:
r0
I str  2  u (r )  (r )dr
0
Questa corrente può essere osservata solo se le estremità del capillare sono
connesse attraverso un circuito esterno a bassa resistenza (condizioni di corto
circuito).
Se questa resistenza fosse elevata (circuito aperto), il trasporto di ioni mediante
questa corrente porta all’accumulo di cariche di segno opposto tra le due estremità
del capillare, con conseguente formazione di una differenza di potenziale attraverso
la lunghezza del capillare.
Questa differenza di potenziale è detta streaming potential Ustr e produce una
corrente di conduzione IC:
z DPA
IS 
4ml
Il valore dello streaming potential è ottenuto dalla condizione di uguaglianza tra la
corrente di conduzione e la streaming current, che corrisponde alla scomparsa
della corrente netta:
z DP
D 
4mx
x=conduttività del bulk
La teoria è incompleta perchè:
•non include il trattamento delle superfici fortemente curvate ( superfici per cui la
condizione ka>>1 non è valida)
•trascura l’effetto della conduzione superficiale sia per la parte dello strato compatto
(IHP) che per lo strato diffuso (OHP) del doppio strato elettrico
•trascura la polarizzazione del doppio strato
Per quanto riguarda il primo punto, la teoria si basa sull’assunzione che
l’interfaccia sia piatta o che il raggio di curvatura in qualunque punto è molto
più grande dello spessore del doppio strato elettrico.
Se questa condizione non è soddisfatta la teoria di Smoluchovski non è valida,
indipendentemente dal fatto si consideri o meno la conduzione superficiale.
Per quanto riguarda la conduzione superficiale esiste un trattamento dettagliato e
riguarda molto le metodologie di misura. Inoltre diventa importante per valori del
potenziale z elevati.
La polarizzazione del doppio strato comporta l’accumulo di cariche di eccesso su
un lato della particella e diminuzione sull’altro. Il dipolo risultante determina una
distribuzione del campo elettrico sovrapposta al campo applicato, influenzando il
moto relativo solido/liquido. L’estensione della polarizzazione dipende dalla
conduttività superficiale.
Any solid in contact with a liquid acquires
some immobilized charge on its surface by
dissociation, complexation, or adsorption.
The immobile charge on the surface
attracts an exact number of excess ions
from the liquid to shield the surface
charge in order to make the interface
neutral. This is the basic mechanism of
formation of the so-called electrical double
layer. One layer is the plane of charge and
the other is a space charge distribution
held near the solid by a balance between
electrostatics and diffusion. One
consequence of this space charge
distribution is that a position-dependent
electrical potential within it varies from
zero far from the surface and reaches a
maximum in magnitude very near the
surface.
The zeta potential of a surface is the value
of this position-dependent electrical
potential within the space charge region at
the plane of shear, i.e. the location near the
surface where the local velocity deviates
from zero when there is flow of liquid in the
vicinity of the surface. This specification
arises from the method by which one
commonly deduces the zeta potential of a
planar surface. One typically measures a
streaming potential near the surface that
arises when liquid flows by it, sweeping
mobile charge in the diffuse layer along
with it. An equation depending on the details
of the system then converts the measured
streaming potential to zeta potential.
Because the streaming potential depends on
shearing the fluid adjacent to the surface,
and because only charge that is outside the
plane of shear contributes to the streaming
potential, the zeta potential is naturally
associated with the plane of shear.
The zeta potential is the electric
potential at the plane of
shear. Since zeta is typically probed
and measured based on its response
to motion of a solid relative to a
liquid, one must realize that there
are cases where the Outer
Helmholtz Plane is not co-planar with
the plane of shear, as shown in the
graphic below. For example, if there
is a brushy polymer adsorbed that is
itself uncharged, the part of the
diffuse layer charge that is inside
the brushy layer does not necessarily
move when fluid flows near it.
Diffuse layer charge that does not
move laterally in response to
shear does not contribute to the
streaming potential and thus does
not contribute to zeta. In many if
not most circumstances, the zeta
potential is essentially equivalent to
the potential at the OHP.
The zeta potential is the overall charge a
particle acquires in a specific medium.
•The magnitude of the zeta potential gives
an indication of the potential stability of
the colloidal system
•If all the particles have a large negative or
positive zeta potential they will repel each
other and there is dispersion stability
•If the particles have low zeta potential
values then there is no force to prevent the
particles coming together and there is
dispersion instability
•A dividing line between stable and unstable
aqueous dispersions is generally taken at
either +30 or -30mV
•Particles with zeta potentials more positive
than +30mV are normally considered stable
•Particles with zeta potentials more
negative than -30mV are normally
considered stable
•The most important factor that affects zeta
potential is pH
•A zeta potential value quoted without a definition
of it's environment (pH, ionic strength,
concentration of any additives) is a meaningless
number
Imagine a particle in suspension with a negative
zeta potential
•If more alkali is added to this suspension then
the particles tend to acquire more negative charge
•If acid is added to this suspension then a point
will be reached where the charge will be
neutralized
•Further addition of acid will cause a build up of
positive charge
•In general, a zeta potential versus pH curve will
be positive at low pH and lower or negative at high
pH
•There may be a point where the curve passes
through zero zeta potential
•This point is called the isoelectric point and is
very important from a practical consideration
•It is normally the point where the colloidal
system is least stable
if the dispersion pH is below 4 or
above 8 there is sufficient charge
to confer stability. However if the
pH of the system is between 4
and 8 the dispersion may be
unstable. This is most likely to be
the case at around pH 6 (the
isoelectric point)
I globuli rossi, pure essendo presenti nel
sangue in quantità elevatissime non
vengono mai a contatto tra loro perché
sulla loro membrana sono presenti cariche
elettriche negative: c'è quindi una continua
repulsione tra loro. Per far sì che dei
globuli rossi agglutinino, quindi, è
necessario che tra un globulo rosso e gli
altri si creino dei ponti abbastanza lunghi
tali da poter vincere la forza di repulsione
delle cariche negative: questi ponti sono
degli
anticorpi,
specialmente
le
immunoglobuline della classe IgM che
sono sufficientemente lunghe.
L’agglutinazione è causata dalla formazione ponti tra i globuli rossi con
la produzione di un agglomerato più o meno grande di emazie di
consistenza simil-gelatinosa.
La fase di agglutinazione è a sua volta influenzata da diversi fattori
alcuni dei quali sono legati alla natura dell’antigene e dell’anticorpo
(numero dimensioni) altre legate alle caratteristiche della superficie
dei globuli rossi ed al bilancio delle forze di attrazione e di repulsione, e
quindi la distanza minima raggiungibile tra gli stessi.
Il numero e localizzazione dei siti antigenici
Dimensioni e struttura dell’anticorpo
Il rapporto tra Antigene-Anticorpo
La distanza tra le cellule
Fattori che intervengono nella fase di agglutinazione
1) Il numero e localizzazione dei siti antigenici: maggiore il numero di
siti antigenici maggiore è il numero di ponti che si possono creare tra le
emazie.
2) Dimensioni e struttura dell’anticorpo: gli anticorpi dalle dimensioni
più grandi, quali le IgM, creano ponti tra i globuli rossi con più facilità.
Inoltre ed ovviamente anche il maggior numero di siti leganti facilitano
l’agglutinazione tra più emazie: le IgM sono costituite da 5 unità ed
esprimono quindi dieci siti leganti e per questo motivi possono creare
agglutinazioni macroscopiche con grande facilità.
3) Il rapporto tra Antigene-Anticorpo: la creazione di ponti tra le
emazie da parte degli anticorpi in soluzione è ottimale quando vi sono
circa 80 parti di anticorpi per una parte di antigene.
4) La distanza tra le cellule: la creazione di ponti da parte degli
anticorpi è possibile solo se i globuli rossi sono abbastanza vicini.
Nelle metodiche in tubetto od in micro colonna si utilizza la
centrifugazione delle sospensioni di globuli rossi per compattare le
cellule e facilitare ed accelerare la formazione di agglutinati.
I globuli rossi tenderebbero ad aggregarsi spontaneamente in virtù
della tensione di superficie, questa tendenza è contrastata dalla
forza di repulsione esercitata dalle cariche elettrostatiche che
circondano le emazie. Gli acidi sialici che ricoprono la superficie degli
eritrociti infatti caricano negativamente i globuli rossi quindi tendono
a respingersi, questa forza elettrostatica di repulsione è chiamato
potenziale Z.
I cationi presenti in soluzione tendono a disporsi intorno alle cariche
negative neutralizzando e riducendo in parte la forza negativa di
repulsione (potenziale Z) e quindi la distanza minima raggiungibile dai
globuli rossi tra di loro.
Per esempio: in soluzione fisiologica (0,9% NaCl) il potenziale Z è -18
mV, che corrisponde ad una distanza di 18-20 nm. A questa distanza
solo le IgM , più grandi) riescono a “fare ponte”, per le IgG invece è
necessario che la distanza sia ridotta sotto i 13 nm, e cioè che il
potenziale Z sia inferiore ai 13 mV
Il potenziale Z può essere influenzato in tre maniere:
Variando la forza ionica: aumentare gli ioni presenti in soluzione avrebbe l’effetto di
abbassare il potenziale Z ma come detto l’aumento della forza ionica avrebbe l’effetto
paradosso di diminuire il legame Ag-Ac: per questo si preferisce comunque utilizzare le
soluzioni LISS a bassa forza ionica.
Variando la costante dielettrica del mezzo mediante macromolecole solubili come
l’albumina, oppure utilizzando polimeri policationici quali il polibrene e solfato di
protamina. Con il polibrene le forze di repulsione sono quasi annullate e le emazie
agglutinano spontaneamente permettendo così, data la distanza ridotta, la formazione di
legami da parte anche di IgG. l’aggiunta successiva di sali neutri quali il sodio citrato
annulla l’effetto “agglutinante” del polibrene: la persistenza della agglutinazione indica
quindi la presenza di anticorpi “cross linked”.
Modificando la carica elettrica superficiale dei globuli rossi: l’utilizzo di enzimi
proteolitici (ficina, bromelina, papaina, tripsina) permette di rimuovere le proteine cui
sono legati gli acidi sialici. Il trattamento proteolitico inoltre è in grado da un lato di
rendere più accessibili alcuni antigeni (es. Rh ). Alcuni antigeni vengono però distrutti
dal trattamento proteolitico (es. antigeni M,N,S, e sistema Duffy) e per questo il metodi
enzimatico non è indicato per lo screening degli anticorpi.
VELOCITA’ DI
ERITROSEDIMENTAZIONE
(VES)
Se il sangue periferico prelevato è reso incoagulante
e lasciato in una provetta, i suoi globuli rossi tendono
a sedimentare spontaneamente.
Già gli antichi greci osservarono che gli eritrociti del
sangue periferico di persone gravemente ammalate
sedimentavano al fondo del contenitore più
rapidamente degli eritrociti del sangue di persone
normali con formazione di un deposito scuro
chiamato “bile nera”
L’influenza del campo gravitazionale terrestre è
osservabile solo con particelle sufficientemente
pesanti e se queste sono sospese in un mezzo
fluido, la velocità finale di caduta è determinata
da bilancio tra la forza gravitazionale e la
resistenza di attrito del mezzo fluido al
movimento della particella.
La velocità gravitazionale delle emazie nel campo
gravitazionale terrestre dipende dal peso
specifico delle emazie che è superiore di poco a
quello del mezzo in cui sono sospese, il plasma.
La velocità di sedimentazione secondo la legge di Stokes
per particelle ideali sferiche è il doppio del quadrato del
raggio, questa legge può essere ritenuta valida anche nel
caso di particelle non sferiche e molto concentrate come i
globuli rossi e che tendono ad aggregarsi o come si dice ad
“impilarsi”, cioè a formare degli ammassi simili a pile di
monete ( detti in francese rouleaux) allineati lungo un
singolo asse perpendicolare al piano della cellula.
Tanto più le emazie si organizzano in questo modo, tanto più
aumenta la loro velocità di sedimentazione
Pertanto la VES non indica soltanto una variazione delle
proteine del plasma, ma riflette anche le variazioni
dell’ematocrito e dipende dalla deformità ed aggregabilità
delle emazie.
Infatti la sedimentazione dipende anche da:
Concentrazione delle particele
Dalla temperatura (in genere sopra 20°C la legge di Stokes
non funziona)
Dalle variazioni di densità delle particele.
La tendenza delle emazie ad aggregarsi dipende in parte dalla
loro forma e dimensione: le normali emazie biconcave tendono ad
aggregarsi più facilmente delle emazie caratteristiche di alcune
anemie, (con sferocitosi, acantocitosi, falcemia) in cui si
dovrebbe avere un ritardo di VES.
Anche la concentrazione delle emazie, che
condiziona la viscosità del sangue, tende ad
influenzare la VES:
la policitemia fa aumentare la viscosità e quindi la
tendenza delle emazie a rimanere in sospensione
ritardando la VES,
al contrario le anemie gravi accelerano la VES
( in assenza di altri fattori se l’ematocrito è inferiore al
20%)
La poca predisposizione delle emazie normali ad aggregarsi
dipende principalmente dal fatto che :
La forza di Van der Waals che favorisce la coesione tra le
emazie, è bilanciata o in parte superata dalle cariche negative
della membrana cellulare (potenziale zeta) che tendono a
respingere le emazie.
Nei g.r. il potenziale zeta (strato di cariche che possono essere
dello stesso segno o di segno opposto) va da 20 a 25 MV, le
proteine dissolte o adsorbite sulla superficie del g.r. abbassano
il potenziale zeta;
ad un potenziale di 15 MV si ha aggregazione eritrocitaria
Le proteine fibrose asimmetriche (fibrinogeno α
e γ-globuline) determinando una ragnatela tra le
particelle, fanno aumentare la viscosità e quindi
si dovrebbero opporre alla sedimentazione, ma
poiché formano grossi aggregati (con le loro
cariche positive diminuiscono il potenziale zeta),
esse favoriscono la sedimentazione.
I metodi elettrochimici si basano sulla misura della risposta elettrica fornita
dal campione (in soluzione) quando viene inserito in un sistema
elettrochimico, ovvero un insieme opportunamente strutturato di conduttori
di prima e di seconda specie.
Un sistema elettrochimico, in sostanza, è costituito da tre componenti
principali un circuito esterno, gli elementi sensibili (o elettrodi) e l'oggetto di
analisi (o analita), che in genere è una soluzione elettrolitica.
I parametri su cui si opera o che
vengono misurati sono:
- potenziale e differenza di
potenziale (simbolo, Vo E.);
- intensità di corrente (i);
- quantità di carica elettrica (q);
- resistenza (R) oppure conduttanza
(A).
CLASSIFICAZIONE DEGLI ELETTRODI
Gli elettrodi impiegati per la misurazione dell'attività di un certo analita sono chiamati
elettrodi indicatori.
Un elettrodo indicatore ideale dovrebbe rispondere rapidamente e in modo
riproducibile ad ogni variazione di attività dell'analita in esame. In pratica è spesso
possibile che un elettrodo di misura risponda anche a variazioni di attività di altre
specie, che non sia cioè perfettamente specifico, o che risponda solo lentamente.
Per misurarne il potenziale, gli elettrodi indicatori devono essere accoppiati ad un
elettrodo di riferimento, cioè ad un elettrodo a potenziale noto, Vrif, in modo che dal
valore sperimentale della differenza di potenziale misurata ai capi della cella
elettrochimica così realizzata, DV, si possa risalire per differenza al potenziale
dell'elettrodo indicatore.
Gli elettrodi di riferimento ideali dovrebbero avere un potenziale noto e costante
(anche qualora la cella sia attraversata da una corrente elettrica di bassa intensità)
oltre che indipendente dalla composizione della soluzione in cui deve essere
immerso.
Entrambi i tipi di elettrodi dovrebbero essere di facile costruzione e robusti. Non tutte
queste condizioni possono essere rispettate rigorosamente.
109
Classificazione degli Elettrodi
• Sulla base della natura e del numero di
fasi tra cui avviene il trasferimento
elettronico
• 3 Classi:
– Elettrodi del I tipo
– Elettrodi del II tipo
– Elettrodi del III tipo
– Elettrodi del IV tipo
Gli elettrodi di Ia specie
M/Mn+
sono costituiti da un metallo immerso in una soluzione di suoi ioni. La corrispondente
reazione elettrodica è la seguente
Mn+ + ne- = M
L'elettrodo di zinco e quello di rame usati nella pila Daniell sono di Ia specie.
L'equazione di Nernst per questi elettrodi è del tipo
V  V +
0,059
log(aMn+ )
n
V  V +
0,059
log[Mn+ ]
n
Il potenziale degli elettrodi di Ia specie dipende quindi dall'attività dei cationi del
metallo elettrodico.
Un elettrodo di Ia specie ad Ag/Ag+ può essere utilizzato per misurare il pAg nel corso
di una titolazione di precipitazione dei cloruri.
NOTE: gli elettrodi in Fe, Al, e W NON SONO elettrodi del I tipo
perchè presentano una copertura superficiale relativamente spessa
di ossido.
111
Gli elettrodi di IIa specie
M/MxAy(s)/Axsono costituiti da un metallo ricoperto da un suo sale poco solubile e immerso in una
soluzione contenente l'anione del sale poco solubile.
Due esempi importanti sono
l'elettrodo Ag/AgCl/Cl- (V° =
0,222 V) e quello a calomelano
Hg/Hg2Cl2/Cl- saturo (standard
calomel electrode, SCE, V° =
0,268 V).
Le reazioni elettrodiche sono,
rispettivamente
AgCl + e- = Ag + ClHg2Cl2 + 2e- = 2Hg + 2Cl-
KCl
Setto poroso
112
Ag/AgCl, KCl
Il sale insolubile è AgCl sottoposto all’equilibrio di solubilità:
AgCl  Ag + + Cl - 
+
-
K PS  [ Ag ][Cl ]  a Ag + aCl - 
a Ag +
K PS

aCl -
La reazione redox corrispondente è:
+
-
-
Ag + Cl + e  Ag + Cl
Essendo insolubile è presente
come corpo di fondo o deposito
sul metallo
aAg+=1
-
Il potenziale redox è relativo alla coppia Ag/Ag+:
E Ag / Ag +  E
0
Ag / Ag +
0
E Ag / Ag +  E Ag
/ Ag +
E
0'
Ag / Ag +
E
0
Ag / Ag +
0'
E Ag / Ag +  E Ag
/ Ag +
RT
+
ln a Ag + 
F
RT K PS
RT
RT
0
+
ln
 E Ag / Ag + +
ln K PS ln aCl F
aCl F
F
RT
+
ln K PS
F
RT
ln aCl F
Dalle reazioni elettrodiche è facile ricavare le equazioni di Nernst
V(Ag/AgCl,Cl-) = V° (Ag/AgCl,Cl-) - 0,059 log aClV(Hg/Hg2Cl2,Cl-) = V° (Hg/Hg2Cl2,Cl-) - 0,059 log aClIl potenziale degli elettrodi di IIa specie dipende quindi dall'attività degli anioni
del sale poco solubile.
Gli elettrodi di IIa specie sono usati spesso come elettrodi di riferimento. Si
pensi ad un elettrodo ad Ag/AgCl/Cl- immerso in una soluzione satura di KCl:
dato che la concentrazione di cloruro è costante in quanto determinata dal
prodotto di solubilità del AgCl, il potenziale elettrodico è costante (e tale rimane
ammesso che l'elettrodo non venga attraversato da una quantità di corrente
così elevata da modificare significativamente la concentrazione del cloruro).
115
The Calomel Reference
Electrode
Electrode
Acronym
Hg(l)/Hg2Cl2(s)/KCl (0.1 M)
Hg/Hg2Cl2(s)/KCl (1 M)
Hg(l)/Hg2Cl2(s)/KCl (sat'd)
Hg(l)/Hg2Cl2(s)/ NaCl (sat'd)
NCE
SCE
SSCE
Potential vs.
SHE
0.3337
0.2801
0.2412
0.2360
Note: concentrations typically high  D concentrations
small  electrode doesn’t become polarized  potential
constant
Electrode of the Third Kind
• Electrodes that merely serve as sources or
sinks for electrons
• Common names: redox, inert, unattackable
• EXAMPLES:
– metals: Pt, Au, GC, graphite, HOPG, Hg
– semiconductors: Si, GaAs, In-SnO2/glass
• Response:
– for Pt in contact with Fe2+, Fe3+ in solution:
– E = E0- 0.059 (V) log ([Fe2+]/[Fe3+])
Gli elettrodi metallici inerti per sistemi redox sono costituiti da un conduttore
metallico inerte (Pt, Au) immerso in una soluzione contenente entrambe le
specie di una coppia di ossidoriduzione. Due elettrodi di ossidoriduzione sono i
seguenti
Pt/Fe3+, Fe2+
Pt/MnO4-, Mn2+, H+
Le corrispondenti reazioni elettrodiche sono
Fe3+ + e- = Fe2+
MnO4- + 8H+ + 5e- = Mn2+ + 4H2O
e le equazioni di Nernst sono
VFe
aFe3 +
0,059
 V Fe +
log
1
aFe2+
VMn
aMnO - (aH+ )8
0,059
4
 V Mn +
log
5
aMn2+
Gli elettrodi a gas sono elettrodi di ossidoriduzione nei quali uno dei componenti della coppia di
ossidoriduzione è presente allo stato gassoso a pressione e temperatura ambiente. L'elettrodo a
idrogeno è il più noto tra quelli a gas.
118
Electrode of the Fourth Kind
• Electrodes that cannot be classified as 1-3
• EXAMPLES:
– Chemically modified electrodes (CME’s)
Gli elettrodi a membrana sono elettrodi strutturalmente diversi da tutti quelli
finora descritti. In questo contesto è sufficiente sapere che una cella per misure
di pH mediante elettrodo a vetro può essere schematizzata come segue
All'interno dell'elettrodo a vetro è contenuto un elettrodo di riferimento ad
Ag/AgCl/Cl-, che pesca nella soluzione di riferimento di HCl 0,1 M saturata con
KCl. La membrana di vetro separa la soluzione interna da quella esterna. Il
circuito viene chiuso da un secondo elettrodo di riferimento a calomelano o ad
Ag/AgCl/Cl-, immerso nella stessa soluzione a pH incognito tramite un ponte
salino. La differenza di potenziale misurata è quella tra l'elettrodo di riferimento
interno e quello esterno.
In accordo a quanto detto sulle convenzioni dei segni, qui il potenziale è indicato con la lettera V e
non con la lettera E.
120
p. 349
La cella di misurazione può essere congegnata in modo tale che
il secondo elettrodo di riferimento sia contenuto nello stesso
corpo dell'elettrodo a vetro: in tal caso l'elettrodo a vetro
risultante si dice combinato e, in effetti, è una cella
elettrochimica, non un semplice elettrodo (la misurazione
avviene immergendo nella soluzione il solo elettrodo combinato).
121
Il potenziale di membrana risulta dalla composizione di due differenze di
potenziale originate a ciascuna interfaccia elettrodo/soluzione in conseguenza
delle reazioni:
+
(H+ Gl - )si  Hacq
+ (Gl - )si
+
(H+ Gl - )se  Hacq
+ (Gl - )se
I pedici i ed e indicano la superficie
interna ed esterna, rispettivamente.
È stato dimostrato che gli ioni H+ coinvolti nelle reazioni NON attraversano la
membrana di vetro.
Il potenziale misurato dall'elettrodo a vetro, Vg, è quello sviluppato attraverso la
membrana vetrosa
Vg  Ve - Vi  0,0592  log
aH+
e
aH+
i
Dato che l’attività dello ione idrogeno all’interno dell’elettrodo è costante
Vg  -0,0592  logaH+ + 0,0592  logaH+
i
e
Vg  L'-0,0592  pH
122
Variando opportunamente la composizione del vetro è possibile rendere la
membrana sensibile alla variazione di altri ioni (Na+, K+, ecc.). Esistono inoltre
elettrodi a membrana:
a stato solido, nei quali la membrana è uno strato uniforme di un'opportuna
sostanza solida omogenea (per esempio gli elettrodi a cloruro, bromuro,
ioduro e fluoruro);
a membrana plastica (per esempio gli elettrodi sensibili allo ione calcio, al
nitrato ecc.);
a membrana per gas, nei quali il gas dissolto in soluzione (NH3, CO2)
diffonde, attraverso una membrana opportuna, in un piccolo volume di
soluzione tampone specifica: la reazione del gas con il tampone provoca la
variazione di pH rilevata dall'elettrodo a vetro per pH contenuto all'interno
dell'elettrodo a gas;
In definitiva, gli elettrodi a membrana, o elettrodi iono-specifici (ISE: ion specific
electrodes) disponibili sul mercato permettono la determinazione di cationi (Cd2+,
Ca2+, Cu2+, Pb2+, Ag+, ecc.), anioni (alogenuri, CN-, NO3-, NO2-, ClO4-, S2-, ecc.) e
specie gassose (NH3, CO2, Cl2, O2, ecc.).
Dato che gli elettrodi a vetro e molti elettrodi a membrana presentano una
resistenza elettrica molto elevata (nella maggior parte dei casi compresa tra 10 e
100 M), le misure di pH richiedono l'uso di voltmetri elettronici aventi una
resistenza interna particolarmente elevata.
123
Elettrodi iono-selettivi
(ISE)
• Un elettrodo iono-selettivo è una semi-cella
elettrochimica (galvanica) il cui voltaggio è
funzione dell’attività (concentrazione) di uno
specifico ione
• La specificità dipende dalla membrana
• Va considerata la selettività dell’elettrodo
Elettrodi iono-selettivi
(ISE)
elettrodo di
riferimento
Per un elettrodo iono-selettivo,
il voltaggio è:
• E* è costante per un dato elettrodo
• z è la carica dello ione considerato
Applicazioni degli ISE
• Na+
• Acque marine, siero, suolo
• K+
• Siero
• Ca2+
• Siero; birra, latticini
Cl-
•
• NO3• F• NH4+
• Test per fibrosi cistica; alimenti
• Acque potabili e reflue; fertilizzanti
• Acque potabili e reflue
• Kjeldhal; dosaggio dell’urea
Elettrodo ad ossigeno
Un comune elettrodo ad ossigeno è l’elettrodo di Clark:
 catodo (elettrodo di lavoro) di platino o d’oro,
 anodo (elettrodo di riferimento) di Ag/AgCl,
separati da una resina epossidica isolata.
I due elettrodi sono fissati in un supporto di plastica contenente una
soluzione elettrolitica.
Il tutto è separato dalla soluzione esterna, in cui verrà addizionato il
campione da misurare, da una membrana gas permeabile (membrana di
teflon). L’elettrodo di lavoro è mantenuto ad un potenziale di circa -700
mV rispetto all’elettrodo d’argento ed è posto in intimo contatto con la
membrana a gas al fine di ottenere una risposta rapida. In queste
condizioni si registra una variazione di corrente dovuta alla riduzione
dell’ossigeno al catodo secondo la seguente reazione:
Pt= catodo
O2 + 4H++ 4e-  2 H2O
mentre all’anodo Ag/AgCl
4Ag + 4Cl- 4AgCl + 4e-
L’elettrodo ad ossigeno (di Clark)
• Catodo di platino
• Membrana permeabile all’ossigeno
• Viene applicata una differenza di potenziale
costante
• L’ossigeno diffonde al catodo e si riduce
• La corrente prodotta è proporzionale ad [O2]
Cella di Clark
Applicazioni dell’elettrodo
ad ossigeno
• Studi su mitocondri
–
–
•
•
•
•
•
controllo respiratorio
inibitori
Misure di perossidazione
Studi su cloroplasti
Dosaggi enzimatici
Studi ambientali
Studi clinici (emogasanalisi, macchina cuorepolmoni)
• Dosaggi con biosensori
• Fermentatori
Reference Electrodes
• Purpose: provide stable potential
against which other potentials can be
reliably measured
• Criteria:
– stable (time, temperature)
– reproducible (you, me)
– potential shouldn’t be altered by passage
of small current = not polarizable
– easily constructed
– convenient for use
SHE
Advantages
• International
standard E0  0 V
• One of most
reproducible
potentials + 1 mV
Disadvantages
• Convenience
– Pt black easily
poisoned by
organics, sulfide,
cyanide, etc.
– Hydrogen explosive
– Sulfuric and
hydrochloric strong
acids
Practical Reference Electrodes
Aqueous
• SCE
• Ag/AgCl
Nonaqueous
• Ag+/Ag
• pseudoreferences
– Pt, Ag wires
• Ferrocene
SCE
• Cl-(aq)/Hg2Cl2/Hg(l)
• Hg22+ + 2e- = 2Hg(l)
• E0 = 0.24 V vs. SHE @ 250C
Advantages
• Most
polarographic
data ref’d to
SCE
Disadvantages
• Hg toxic
• solubility of KCl
temperature
dependent dE/dT
= -0.67 mV/K
(must quote
temperature)
Ag/AgCl
• Ag wire coated with
AgCl(s), immersed in
NaCl or KCl solution
• Ag+ + e- = Ag(s)
• E0 = 0.22 V vs. SHE @
250C
Advantages
• chemical
processing
industry has
standardized on
this electrode
• convenient
• rugged/durable
Disadvantages
• solubility of
KCl/NaCl
temperature
dependent
dE/dT = -0.73 mV/K
(must quote
temperature)
Ag+/Ag
• Ag+ + e-= Ag(s)
• requires use of internal potential
standard
Advantages
• Most widely used
• Easily prepared
• Works well in all
aprotic solvents:
– THF, CAN,
DMSO, DMF
Disadvantages
• Potential depends
on
– solvent
– electrolyte (LiCl,
TBAClO4, TBAPF6,
TBABF4
• Care must be taken
to minimize
junction potentials
Pseudo-References
• Pt or Ag wire (inert)
• Idea:
in medium of high resistance, low
conductivity, wire will assume
reasonably steady, highly reproducible
potential (+ 20 mV)
• Advantage: no solution contamination
• Limitation: must use internal potential
standard (ferrocene)
Can Aqueous References Be
Used in Nonaqueous Media?
• Yes with caution!
– May be significant junction potentials
• Requires use of internal standard
– May be greater noise
• Electrolyte may precipitate/clog electrode frit
– Don’t forget about your chemistry
• Chemistry may be water sensitive
Electrodes
• Metal
– solid
• Pt, Au, Ag, C
– liquid
• dropping mercury electrode (DME)
• Semiconductors
– Si, GaAs
– In-SnO2/glass (optically transparent)
Carbon
• Paste
– With nujol (mineral oil)
• Glassy carbon (GC)
– Amorphous
• Pyrolytic graphite - more ordered than GC
– Basal Plane
– Edge Plane (more conductive)
Electrode Materials
• Different Potential Windows
• Can affect electron transfer kinetics
Electrodes
• Size
– Analytical macro
• 1.6 - 3 mm diameter
– Micro
• 10-100 mm diameter
– UME
• <5 mm diameter
Electrode Geometry
Geometry is critical and affects how the
data are analyzed and interpreted
Note: Geometric area <
• Disk
– area: r2
• wire (cylinder)
– area: l(2 r) r2
• Mesh
– optically transparent
• Sheet
effective surface area
Cleanliness IS Next to “Goodliness”
in Electrochemistry
• Working electrode must be carefully
cleaned before each experiment
– Mechanical
• Abrasion with alumina or “diamond” polish
– Chemical
• Sonicate in Alconox
• Soak in HNO3
– Electrochemical
• Cycle in 0.5 M H2SO4 (Pt)
Cleanliness
Mechanical
Abrasion with
alumina or
“diamond” polish
Electrochemical Cleaning
Taken from Table 4-7 in Sawyer, D.T.; Roberts, Jr., J.L. Experimental
Electrochemistry for Chemists Wiley: New York, 1976.
Counter Electrode
• Area must be greater
than that of working
• Usually long Pt wire
(straight or coiled) or
Pt mesh (large
surface area)
• No special care
required for counter
Ew = Ecell - iRcell - Epolarization
When is iR large?
•I is high, I > 10 mA
•large electrodes
•solvents with low conductivity
•relatively polar organic solvents
Two Common Configurations
• 2-electrode cell
– iR must be small < 1 mV
(microelectrodes)
• 3-electrode cell
– Avoids internal
polarization of reference
electrode
– Compensates for major
potion of cell iR drop
2-Electrode Cell
• 2-electrode cell
– Working
– Reference electrode
• Current passed between working and
reference
3-Electrode Cell
• 3-electrode cell
– Working
– Reference
– Counter/auxilliary
• Current is passed between working and
counter
• High impedance placed in front of
reference (low current) so ref. Potential
constant
Potentiostat/Galvanostat
• Potentiostat
– Control potential
– Cyclic voltammetry,
chronoamperometry,
etc.
• Galvanostat
– Control current
– Potentiometry