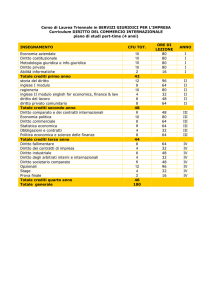
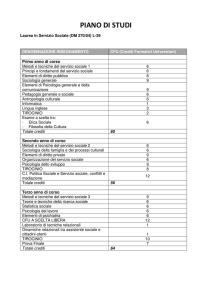
!I ANNO - I SEMESTRE !
Calcolo 1 - 7 crediti (Prof. A. Porretta)
Numeri reali e complessi. Funzioni. Limiti. Successioni e serie. Funzioni continue. Derivata, retta
tangente. Massimi, minimi, studio di funzioni. Regola di De l'Hopital. Polinomio di Taylor e
applicazioni. Integrale di Riemann, teorema fondamentale del Calcolo. Metodi di integrazione. Integrali
impropri.
TESTI CONSIGLIATI !E. Giusti (Analisi Matematica 1,Bollati Boringhieri)!E. Giusti (Esercizi e
complementi di analisi matematica 1,Bollati Boringhieri,) !B. Demidovich (Esercizi e problemi di Analisi
Matematica,Ed. Riuniti)
Calcolo 1 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo differenziale e integrale
per le funzioni di una variabile. Calcolo combinatorio, numeri complessi, funzioni elementari in campo
complesso. L'oscillatore armonico smorzato !
Calcolo 2 - 5 crediti (Prof. F. Fidaleo - richiede il superamento di Calcolo 1)
FUNZIONI DI DUE VARIABILI. Grafici, curve di livello, continuità e limiti. Insiemi di punti del piano:
frontiera, insiemi aperti, chiusi, limitati e connessi: teoremi relativi. Derivate parziali, gradiente,
differenziale, teorema delle funzioni implicite, massimi e minimi liberi e vincolati. Derivate seconde e
successive. Integrali curvilinei, forme differenziali e loro integrazione. !FUNZIONI DI TRE E PIU'
VARIABILI. Estensioni del caso bidimensionale; campi vettoriali.
TESTI CONSIGLIATI !E. Giusti: Analisi Matematica, voll I e II; Bollati Boringhieri, Torino F! . Conti:
Calcolo, teoria e applicazioni, McGraw-Hill !A. Schiaffino, A. Vignoli: Introduzione all'Analisi
Matematica, vol. II; Aracne, Roma !B. Demidovic: Esercizi e problemi di Analisi Matematica; Editori
Riuniti, Roma
Calcolo 2 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo differenziale nel piano e
nello spazio. Integrazione di forme differenziali (grado 1). Formula di Taylor. Successioni e serie.
Corso di lingua inglese - 4 crediti (Prof. F. Fantera)
Main Objectives: The course aims at the consolidation and improvement of the four language skills
(reading, writing, listening, and speaking) through a wide range of activities in the field of science.
Course content: The lessons will be organized around various thematic units based on the course
textbook and articles taken from authentic sources such as newspapers, the internet, specialized
journals and hand-outs distributed in class. Each unit will focus on enhancing general language
structures, vocabulary and functions on the basis of the readings and in class discussions. Particular
attention will be given to improving reading comprehension and summarizing skills.
!Geometria 1 - 7 crediti (Prof. M. Letizia)
Geometria del piano e dello spazio, vettori geometrici rette e piani, equazioni parametriche e
cartesiane, prodotto scalare e vettoriale, generalizzazione allo spazio R^n, sottospazi vettoriali ed
affini di R^n. Sistemi di riferimento. Matrici e determinanti. Risoluzione dei sistemi lineari eliminazione
di Gauss Rango di una matrice e numero dei parametri liberi dello spazio delle soluzioni di un sistema
lineare. Coniche e quadriche in forma canonica Esempi di curve e superfici, equazioni parametriche e
cartesiane.
TESTI CONSIGLIATI !S.Abeasis: Elementi di Algebra Lineare e Geometria; Ed. Zanichelli !M. Abate:
Geometria; Ed. McGraw-Hill
Geometria 1 - 5 crediti (Corso in vigore fino all'a.a. 2002-2003)!Esempi di spazi vettoriali
geometrici e numerici. Geometria analitica nel piano e nello spazio. !Coniche e Quadriche in forma canonica.
Esempi di curve e superfici: equazioni parametriche e cartesiane.
Meccanica 1 - 6 crediti (Prof. P. Chiaradia)
Cinematica e Dinamica del punto materiale (forze, lavoro ed energia, momento angolare, leggi di
conservazione). Moti relativi. Dinamica dei sistemi di punti materali. Urti. Dinamica del corpo rigido.
Cenni di statica
Meccanica 1 - 8 crediti (Corso in vigore fino all'a.a. 2003-2004) !Cinematica e Dinamica del
punto materiale (forze, lavoro ed energia, momento angolare, leggi di conservazione). Moti relativi. Dinamica
dei sistemi di punti e del corpo rigido. cenni di statica.
Matematica 0
Operazioni sui numeri reali. Trigonometria. Equazioni algebriche. Disequazioni.
I ANNO - II SEMESTRE !
Geometria 2 - 7 crediti (Prof. S. Trapani - richiede il superamento di Geometria 1)
Spazi vettoriali, sottospazi. Somme dirette. Teorema di Grassmann. Applicazioni lineari, matrici
associate, cambiamenti di base. Autovalori, autovettori, diagonalizzazione. Prodotti scalari,
disuguaglianza di Schwartz. Basi ortonormalizzazione di Graham-Smith. Matrici associate ad un
prodotto scalare rispetto ad una base. Aggiunto di un operatore, operatori simmetrici, operatori
hermitiani, diagonalizzazione di operatori, teorema spettrale. Matrici ortogonali ed unitarie. Forma
canonica metrica delle iperquadriche.
TESTI CONSIGLIATI !Lang, Algebra lineare, Boringhieri; Silvana Abeasis, Elementi di algebra lineare e
geometria, Zanichelli.
Geometria 2 - 7 crediti (Corso in vigore fino all'a.a. 2002-2003)!Matrici e determinanti.
Sistemi di equazioni lineari ed eliminazione di Gauss. !Spazi vettoriali di dimensione finita. Operatori lineari;
endomorfismi e diagonalizzazione. Spazi vettoriali metrici. Operatori hermitiani ed unitari. Applicazioni allo
studio delle coniche e quadriche.
Laboratorio di Informatica 1 - 4 crediti (Docente da definire)
Cenni sull’architettura di Computer: Introduzione, mod. Von Neumann, modello a Bus, Circuiti
integrati, Livelli di astrazione di un Calcolatore - Memorie: memorie multilivello, memorie cache,
prestazioni delle CPU - Misura delle prestazioni di una CPU (Clock speed, CPI, flops, etc.),
architetture CISC e RISC, cenni sul Codice Macchina, generazione di numeri casuali Rappresentazione in memoria dei numeri: formati intero e virgola mobile, rapprentazione in
complemento a due, addizione, sottrazione e moltiplicazione; Diagrammi di flusso, Programmazione
Strutturata, Progettazione Bottom-Up e Top-Down - Codici ASCII e Unicode, files binari e files
formattati - Memorie secondarie, dischi magnetici e ottici -Comunicazione tra calcolatori: connessioni
seriali, reti, links fisici, protocolli di comunicazione, servizi - Lo Scilab con esercitazioni volte a
risolvere problemi di fisica.
Meccanica 2 - 6 crediti (Prof. P. Chiaradia)
Gravitazione universale. Massa inerziale e gravitazionale. Campo ed energia potenziale gravitazionali.
Leggi di Keplero. Proprietà statiche e dinamiche dei fluidi. Legge di Stevino. Viscosità e fluido ideale.
Teorema di Bernoulli e applicazioni. Oscillazioni e onde. Oscillatore armonico. Oscillazioni forzate e
risonanza Equazione delle onde piane. Onde in una corda tesa.
Meccanica 2 - 4 crediti (Corso in vigore fino all'a.a. 2003-2004)!Gravitazione universale.
Massa inerziale e gravitazionale. Campo ed energia potenziale gravitazionali. Leggi di Keplero.!Proprietà
statiche e dinamiche dei fluidi. Legge di Stevino. Viscosità e fluido ideale. Teorema di Bernoulli e
applicazioni. !Oscillazioni e onde. Oscillatore armonico. Oscillazioni forzate e risonanza Equazione delle onde
piane. Onde in una corda tesa.
Termodinamica - 5 crediti (Prof. P. Chiaradia - richiede il superamento di
Meccanica 2)
Temperatura e termometri. Principio zero. Calore. Primo Principio. Energia interna. Calori specifici.
Cambiamenti di fase. Trasmissione del calore. Gas ideali (Leggi, Equazione di stato, Trasformazioni
cicliche) e Gas reali (Equazione di Van der Waals). Teoria cinetica dei gas. Secondo principio.
Teorema di Carnot. Temperatura termodinamica assoluta. Terorema di Clausius. Entropia. Terzo
principio della termodinamica (cenni). Potenziali termodinamici (cenni).
Termodinamica - 6 crediti (Corso in vigore fino all'a.a. 2002-2003)
Laboratorio 1 - 8 crediti (Prof.ssa R. Bernabei)
Grandezze fisiche. Strumenti di misura e loro caratteristiche. Errori di misura e loro propagazione.
Misure di grandezze meccaniche e termiche connesse alle esperienze di laboratorio. Trattamento
statistico dei risultati di una misura. Probabilità e frequenza. Distribuzioni limite. Metodo dei minimi
quadrati: regressione lineare. Esercitazioni di laboratorio. !
II ANNO - I SEMESTRE !
Elettromagnetismo 1 - 6 crediti (Prof. R. Santonico)
La legge di Coulomb e il campo elettrico. La legge di Gauss. Il potenziale elettrico. Capacità.
Dielettrici. Corrente e resistenza. Circuiti elettrici. Campo magnetico costante nel vuoto. Legge di
Ampère.
Elettromagnetismo 1 - 8 crediti (Corso in vigore fino all'a.a. 2003-2004)!La legge di
Coulomb e il campo elettrico. La legge di Gauss. Il potenziale elettrico. Capacità e dielettrici. Corrente e
resistenza. Circuiti in corrente continua. Campo magnetico nel vuoto. Induzione elettromagnetica.
Autoinduzione e induzione mutua. Campi magnetici nella materia.
Chimica - 7 crediti (Prof.ssa M.L. Terranova)
Struttura della Tavola Periodica. Elementi e composti. Proprietà generali degli elementi dei gruppi
rappresentativi. Formule ed equazioni chimiche. Il legame chimico. Calore e lavoro nei sistemi chimici.
Lo stato di equilibrio: il potenziale chimico, la costante di equilibrio. Equilibrio e reversibilità in
processi chimici e trasformazioni di fase. Le soluzioni. Acidi, basi e sali. Dissociazione ionica e
trasporto di cariche. Le proprietà colligative. Equilibri omogenei 7 ed eterogenei in soluzione acquosa.
Reazioni redox. Celle elettrochimiche. Potenziali elettrodici e forza elettromotrice di una cella.
Elettrolisi. Cenni di cinetica chimica. Cenni di chimica organica.
Calcolo 3 - 9 crediti (Prof. A. Schiaffino - richiede il superamento di Calcolo 2)
Integrali multipli: concetti generali, teorema della divergenza e del rotore. Equazioni differenziali caso
lineare, esponenziale di una matrice. Caso non lineare, integrali primi e loro uso nella ricerca delle
soluzioni. Serie e integrale di Fourier. Trasformata di Laplace
TESTI CONSIGLIATI !M. Bramanti, C.D. Pagani, S. Salsa Matematica (seconda edizione) Zanichelli,
Bologna !E. Giusti: Analisi Matematica, vol. II; Bollati Boringhieri, Torino !V. Smirnov: Matematiche
Superiori, voll I e II; Editori Riuniti, Roma !N. Piskunov: Calcolo differenziale e integrale; Editori Riuniti,
Roma !B. Demidovic: Esercizi e problemi di Analisi Matematica; Editori Riuniti, Roma
Calcolo 3 - 6 crediti (Corso in vigore fino all'a.a. 2002-2003)!Calcolo integrale nel piano e nello
spazio. Calcolo differenziale in dimensione finita. Equazioni differenziali ordinarie.
Laboratorio di informatica 2 - 6 crediti (Prof. F. Berrilli - richiede il superamento
di Laboratorio di Informatica 1)
Algebra lineare. Matrici. Vettori; metodo di Gram-Schmidt. Determinante di una matrice; regola di
Laplace. Teorema di RouchŽ-Capelli. Autovalori e autovettori, diagonalizzazione di una matrice.
Sistemi lineari con matrice triangolare; fattorizzazione LU, metodo di Gauss, pivotizzazione parziale.
Linguaggio C: applicazioni all'algebra lineare.
II ANNO - II SEMESTRE !
Elettromagnetismo 2 - 6 crediti (Prof. R. Santonico)
Campo magnetico costante nella materia. Induzione elettromagnetica. Autoinduzione e induzione
mutua. Correnti alternate. Oscillazioni elettriche. Equazioni di Maxwell. Onde elettromagnetiche.
RelativitaÕ Speciale e Invarianza relativistica delle equazioni di Maxwell.
Elettromagnetismo 2 - 4 crediti (Corso in vigore fino all'a.a. 2003-2004) ! Circuiti in
corrente alternata. Le equazioni di Maxwell e le onde elettromagnetiche. La Relatività Speciale.
Laboratorio 2 - 8 crediti (Prof. M. Cirillo - richiede il superamento di Laborat. 1)
Leggi di Ohm e di Joule. Analisi dei circuiti elettrici in c.c. e c.a. Grandezze elettriche e relativi
strumenti di misura. Rappresentazione complessa delle correnti e delle tensioni. Circuiti RL, RC ed
RLC. Diodo e circuiti a diodo. Esercitazioni di laboratorio. Onde elettromagnetiche: rifrazione,
riflessione, interferenza. Ottica geometrica: prisma, diottro, specchio sferico. Misure con sistemi ottici
centrati e strumentazione connessa. Laser. Ottica dei corpi anisotropi.
Laboratorio 2 - 6 crediti (Corso in vigore fino all'a.a. 2002-2003)!Legge di Ohm e di Joule.
Analisi dei circuiti elettrici in c.c. e c.a.. Grandezze elettriche e relativi strumenti di misura. Rappresentazione
complessa delle correnti e delle tensioni. Circuiti RL, RC ed RLC. Diodo e circuiti a diodo. !Approssimazione di
dati sperimentali con curve teoriche: il metodo dei minimi quadrati. Test di conformità di ipotesi. !Esercitazioni
di laboratorio.
Ottica - 3 crediti
Ottica geometrica. Lenti e strumenti ottici. Interferenza. Diffrazione e polarizzazione. Elementi di
ottica dei corpi anisotropi.
!Meccanica analitica - 6 crediti (Prof. L. Triolo - richiede il superamento di Calcolo
3 e Meccanica 1)
Equazioni di Lagrange. Formulazione variazionale. Simmetrie e costanti del moto. Equazioni di
Hamilton. Integrabilitˆ, trasformazioni canoniche, equazione di Hamilton Jacobi.
TESTI CONSIGLIATI !Esposito, Appunti di Meccanica Razionale !Appunti del Docente
Meccanica analitica - 4 crediti (Corso in vigore fino all'a.a. 2002-2003)
!III ANNO - I SEMESTRE !
Meccanica Quantistica 1 - 9 crediti (Prof. M. Bianchi - richiede il superamento di
Calcolo 3, Geometria 2, Meccanica 2, Elettromagnetismo 2 e Meccanica Analitica)
Crisi della Fisica Classica. Corpo nero. Effetto fotoelettrico. Fenomeni ondulatori, interferenza e
diffrazione. Postulati della Meccanica Quantistica. Equazione di Schroedinger unidimensionale: buca di
potenziale, effetto tunnel, oscillatore armonico. Equazione di Schroedinger tridimensionale: atomo di
idrogeno. Momento angolare, composizione dei momenti angolari. Spin e momento magnetico.
Particelle identiche, principio di Pauli. Teoria delle perturbazioni indipendenti dal tempo, teoria delle
perturbazioni dipendenti dal tempo. Metodi variazionali.
Metodi Matematici della Fisica 1 - 9 crediti (Prof. G. Rossi - richiede il
superamento di Calcolo 3, Geometria 2)
Funzioni analitiche di variabile complessa. Teoremi di Cauchy. Funzioni monodrome e polidrome.
Spazi vettoriali ad un numero finito di dimensioni: vettori e operatori lineari. Autovalori e autovettori.
Rappresentazione spettrale. Spazio di Hilbert e cenni di analisi funzionale. Polinomi ortogonali.
Operatore aggiunto, autoaggiunto, unitario e normale. Cenni di teoria delle distribuzioni. Serie e
trasformate di Fourier. Trasformata di Laplace.
Laboratorio Terzo - 6 crediti (soppresso alla fine dell'a.a. 2002/03, corrisponde al
vecchio corso di Laboratorio 3, ridenominato "Terzo" per ragioni amministrative)
Prof. R. Messi (richiede il superamento di Laboratorio 2)
Cenni alla struttura dei semiconduttori. Transistor a giunzione: principali configurazioni e loro
caratteristiche, transistor a basse frequenze, modello ibrido. Amplificatori, amplificatori operazionali e
applicazioni. Rumore in elettronica; tecniche di riduzione del rumore; lock-in. Circuiti digitali; esempi
di funzioni in logica parallela ed in logica seriale. Esercitazioni di laboratorio.
Elementi di Astrofisica 1 - 4 crediti (ex Fisica Moderna 3 - 3 crediti - Prof. F.
Vagnetti)
Le stelle: produzione di energia termonucleare e l'equilibrio stellare; l'energia di Fermi e l'equilibrio
delle nane bianche e delle stelle di neutroni. Sistemi di galassie, quasar; black hole massivi e collasso
gravitazionale; galassie primordiali e storia cosmica dei barioni. Il big-bang; radiazione cosmica di
fondo; nucleosintesi primordiale.
III ANNO - II SEMESTRE !
Struttura della Materia - 8 crediti (ex Fisica Moderna 1 - 6 crediti - Prof. A.
Balzarotti (richiede il superamento di Meccanica Quantistica 1)
Atomi idrogenoidi in campi elettrici e magnetici. Atomi multielettronici. Metodi approssimati.
Iterazione di atomi con il campo di radiazione. Struttura di molecole semplici. Moti elettroni ci e
nucleari. Moti elettronici e nucleari. Spettri molecolari. Solidi: reticolo diretto e reciproco. Struttura a
bande di energia. Semiconduttori. Vibrazioni reticolari.
TESTI CONSIGLIATI !B.H. Bransden, C.J. Joachain: Physics of Atoms and Molecules, Longman (1986).
!C. Kittel: Introduzione alla Fisica dello Stato Solido, Boringhieri (1993). !Appunti distribuiti a lezione.
Elementi di Fisica Nucleare e Subnucleare - 4 crediti (ex Fisica Moderna 2 - 3
crediti - Prof. C. Schaerf)
La scoperta del nucleo atomico. Formula semiempirica delle masse. Modelli nucleari, Deflessione di
particelle cariche sui nuclei ed i raggi nucleari. Cenni sulle particelle elementari.
Meccanica Statistica 1 - 6 crediti (Dr. F. Fucito)
Spazio delle fasi, teorema di Liouville. Ensemble microcanonico. Paradosso di Gibbs. Ensemble
canonico. Ensemble gran-canonico: gas di fotoni e formula di Planck. Condensazione di Bose-Einstein.
Gas di fermioni: degenerazioni di Fermi-Dirac. Applicazioni: gas di elettroni in un metallo, vibrazioni
dei reticoli cristallini e fononi, calori specifici dei solidi.
TESTI CONSIGLIATI !C.J. Thompson Mathematical Statistical Mechanics !G.Parisi Statistical Field
Theory !S.K. Ma Statistical Mechanics !S.K. Ma Modern Theory of Critical Phenomena
Corso a scelta - 6 crediti
Prova finale - 9 crediti
PROGRAMMI DEI CORSI DI FISICA A SCELTA (III ANNO)
Acustica - 6 CFU! (Dr. G. Pucacco)
!Onde in mezzi elastici fluidi e solidi. Velocità del suono. Emissione, propagazione e ricezione del
suono in aria. Sorgenti sonore. Interferenza e diffrazione. Onde stazionarie. Riflessione e
assorbimento del suono. Campi sonori: campo vicino e campo riverberato. Trasmissione del suono e
delle vibrazioni. Sistemi lineari. Equivalenza elettrico-meccanico-acustica. Analisi armonica.
Trasformate di Fourier e Laplace. Funzioni di trasferimento. Risposta in frequenza e nel tempo. Reti di
trasduttori lineari. Linea di trasmissione. !
Elementi di Astrofisica 2 - 6 CFU! (Dott. A. Balbi)
!Il cielo nelle diverse finestre della radiazione elettromagnetica (radio, IR, ottica, X e gamma).
Caratteristiche osservative delle stelle ed atmosfere stellari. Struttura, formazione ed evoluzione delle
stelle. Stati finali dell'evoluzione stellare. Struttura della nostra galassia. Le altre galassie. Nuclei
galattici attivi. Ammassi di galassie e struttura a grande scala dell'universo. Evoluzione dell'universo e
modelli cosmologici.!
Elettronica 1 - 6 CFU! (Dr. A. Florio)
! eti a parametri concentrati - Risposte nel dominio del tempo, della frequenza e della frequenza
R
complessa (Trasformata di Laplace e sue applicazioni) - Teoremi sulle reti- La controreazioneAmplificatori differenziali e operazionali- Applicazioni lineari e non lineari.!
Fisica Biologica 1 - 6 CFU (!Prof.ssa S. Morante)
!La cellula: meccanismi di comunicazione e riconoscimento tra cellule. Le macromolecole: proteine,
acidi nucleici, zuccheri e lipidi. Il messaggio biologico e la doppia elica del DNA: eplicazione,
trascrizione e traduzione. La sintesi proteica. Sequenziamento e mappatura del DNA. Le banche dati.
La post-genomica. DNA e supercomputers: gigabytes e nanotecnologie. Proprietà fisico-chimiche degli
amino acidi. Proteine: funzione e folding. Struttura secondaria e terziaria. Interazione proteinaproteina. Struttura quaternaria e cooperatività: il modello MCW. !
Fisica dei Sistemi Complessi - 6 CFU! (Prof. L. Biferale)
!Fondamenti teorici della meccanica statistica classica: Introduzioni alla meccanica statistica classica. Il
problema ergodico, funzioni di partizione e misura di probabilità. Il teorema del limite centrale e
misura di Gibbs. Sistemi dinamici e teoria delle biforcazioni: Sistemi hamiltoniani a pochi gradi di
libertà. Sistemi dissipativi. Teoria della stabilitˆ alla Lyapunov. Sistemi dinamici a infiniti gradi di libertà.
Solitoni e soluzioni localizzate. Il teorema della varietà centrale in infinite dimensioni. L'equazione di
Laudau-Ginzburg con parametri complessi. Equazioni di Navier Stokes e cenni sulla teoria della
turbolenza sviluppata. !
Fisica Teorica 1 - 6 CFU (!Prof. E. Pace)
Problema di Dirichlet e di Neumann. Eq. di Maxwell. Potenziali ritardati. Tensore degli sforzi di
Maxwell. Onde e.m. Teoria della relativitˆ ristretta. Gruppo e generatori di Lorentz. Covarianza della
elettrodinamica. Lagrangiana per una particella carica e per il campo e.m. Conservazione di energia,
impulso e momento ang. del campo e.m. Tensore degli sforzi. Funzioni di Green. Potenziali di LienardWiechert. Radiazione e.m. !TESTO CONSIGLIATO: !J.D. Jackson "Elettrodinamica Classica", Zanichelli,
2001!
Istituzioni di Fisica Nucleare e Subnucleare - 6 CFU (!Prof.ssa A. D'Angelo)
!Fisica del Nucleo: richiami del modello a shell. Interazione nucleone-nucleone. Il deutone. Reazioni
nucleari. Fisica delle Particelle Elementari: Concetti fondamentali. Stati eccitati e risonanze. Principi di
invarianza, leggi di conservazione e simmetrie. Invarianza CPT. Interazione debole. Neutrini ed
antineutrini. Diffusione pionenucleone. SU(3). I quark costituenti. Teoria del colore e cromodinamica
qunatistica. Mesoni e barioni come stati legati dei quark. Massa degli adroni. !
Complementi di Struttura della Materia - 6 CFU! (Prof. M. De Crescenzi!)
Il corso è diretto a studenti del terzo anno che intendono acquisire una preparazione di base sui
fondamenti sperimentali e teorici della struttura degli atomi e dei solidi. Particolare riguardo sarà dato
alle applicazioni di nuovi fenomeni fisici quali le nanostrutture, la superconduttività ad alta
temperatura, l'STM (scanning tunneling microscopy) e il laser a semiconduttore. !TESTI CONSIGLIATI:
!R. Eisberg e R. Reisnick, "Quantum Physics" per atomi e introduzione storica;!S.M.Sze, "Fisica dei
dispositivi a semiconduttore";!C. Kittel, "Introduzione alla Fisica dello stato Solido".!
Complementi di Ottica - 6 CFU! (Proff. M. Casalboni, F. De Matteis, P. Prosposito)
!Interferenza e diffrazione. Polarizzazione della luce. Ottica all'interfaccia tra due mezzi. Birifrangenza.
Scattering della luce. Quantizzazione del campo elettromagnetico. Coefficienti di Einstein. Teoria
microscopica e macroscopica dell'assorbimento ottico. Indice di rifrazione. Allargamenti di riga. Cenni
di ottica guidata. Guide d'onda dielettriche. Modi ottici. Perdite ottiche in film sottili. Ellissometria
spettroscopica.!TESTI CONSIGLIATI:!R. Loudon The quantum theory of light Oxford Science 1983;!G.
Lifante Integrated Photonics Fundamentals Wiley 2003.
PROGRAMMI DEI CORSI A SCELTA LIBERA (II ANNO) [Consigliati]
Fondamenti dell'Analisi Matematica - 4 crediti
!INSIEMI DI NUMERI REALI
Dai numeri razionali ai numeri reali: definizione formale, classi
numeriche separate, estremi superiore e inferiore di un insieme numerico, serie a termini positivi,
concetto di integrale; esempi.!LIMITI Continuità e limiti per funzioni reali di una variabile reale,
teorema di esistenza degli zeri; spazi normati; completezza e compattezza.!CALCOLO
DIFFERENZIALE Derivate e differenziali per funzioni reali di una variabile reale. Il caso di più
dimensioni. Il teorema delle funzioni implicite. Il teorema di esistenza e unicità per i sistemi di
equazioni differenziali ordinarie.
Complementi di Algebra e Geometria - 6 crediti !
STRUTTURE ALGEBRICHE IN UN INSIEME. La nozione di gruppo . Esempi di gruppi finiti ed i gruppi
classici di matrici. Sottogruppi, omomorfismi ed isomorfismi. Azione di un gruppo su un insieme,
orbite e stabilizzatori. Azioni di un gruppo su se’ stesso: moltiplicazio- ne sinistra, destra e
coniugazione. Definizione di rappresentazione. Un sistema di generatori per il gruppo SO(3,R). I
gruppi di simmetrie dei poliedri regolari ed il gruppo quadratico.!Il gruppo dei movimenti rigidi come
prodotto semidiretto. Definizioni di anello, campo, spazio vettoriale, algebra ed esempi.!STRUTTURE
TOPOLOGICHE IN UN INSIEME. La topologia euclidea. Struttura topologica in un insieme : insiemi
aperti ed applicazioni continue; omeomorfismi. Gruppi topologici e gli esempi dei gruppi classici di
matrici. Connessione, connessione per archi e compattezza; studio dei gruppi classici di matrici con
riferimento a tali nozioni.!GRUPPO DI LORENTZ. Lo spazio di Minkowski R(1,3) e la definizione del
gruppo di Lorentz L(1,3). Il gruppo di Lorentz L(1,1) e le sue orbite sul piano R(1,1). Le orbite del
gruppo di Lorentz L(1,3) sullo spazio di Minkowski. Azione del gruppo SL(2,C) sullo spazio delle
matrici hermitiane 2x2. Generazione del gruppo proprio di Lorentz Lo(1,3) tramite le matrici di
SO(3,R) e le “boost transformations”. L’applicazione SL(2,C) Ò Lo(1,3) come omomor- fismo di
gruppi e come rivestimento doppio del gruppo proprio di Lorentz.!RAPPRESENTAZIONI DEI
GRUPPI. Rappresentazioni irriducibili e completamente riducibili. Rappresentazioni complesse di
gruppi finiti: teoremi generali e teoria dei caratteri. Le rappresentazioni irriducibili dei gruppi delle
permutazioni su 3 e 4 elementi. Cenni alla teoria delle rappresentazioni dei gruppi compatti. Le
rappresentazioni irriducibili dei gruppi compatti SO(2,R) ed SU(2). Il gruppo di Poincare’ come
prodotto semidiretto del gruppo proprio di Lorentz ed R(1,3); il suo rivestimento doppio prodotto
semidiretto di SL(2,C) ed R(1,3). Enunciato del teorema di Wigner: la strategia per calcolare le
rappresentazioni irriducibili del rivestimento doppio del gruppo di Poincare’. Calcolo delle
rappresentazioni irriducibili unitarie che sono riconducibili al caso compatto e cenni al loro legame
con le “particelle elementari”.
Teoria della relatività ristretta - 3 crediti!
Ipotesi dell'etere; esperimento di Michelson-Morley. Contrazione di Lorentz. Postulati della relativita'
ristretta. Esperimenti per mettere in evidenza un eventuale moto rispetto all'etere basati sull'effetto
Doppler e l'effetto Mossbauer. Misura della velocità della luce emessa da pioni in volo. Trasformazioni
di Lorentz. Cono luce; passato, futuro e altrove di un evento. Tempo proprio; dilatazione del tempo;
verifiche sperimentali. Effetto Doppler relativistico.!Composizione delle velocità; quadrivettore
velocita'. Costruzione di impulso ed energia relativistici imponendo la conservazione di impulso ed
energia in urti elastici in ogni sistema di riferimento. Massa a riposo.!Proprieta' dello spazio-tempo.
Gruppo di Lorentz omogeneo e non omogeneo. Scalari, vettori controvarianti e covarianti e tensori
di rango K. Trasformazioni di Lorentz proprie ed improprie. Trasformazioni infinitesime del gruppo di
Lorentz proprio. Generatori delle rotazioni e delle trasformazioni tra riferimenti inerziali in moto
relativo. Regole di commutazione dei generatori di Lorentz.!Invarianza della carica elettrica. Vettore
quadricorrente ed equazione di continuta'. Forma covariante delle equazioni per il quadripotenziale.
Tensore intensita' di campo e tensore duale. Forma covariante delle equazioni di Maxwell nel vuoto e
in un mezzo. Trasformazioni dei campi e.m. per trasformazioni di Lorentz.!Principio di minima azione
ed equazioni di Eulero-Lagrange. Lagrangiana libera e lagrangiana di interazione per una particella
carica in un campo e.m. Momento canonico coniugato; equazioni del moto. Hamiltoniana per una
particella in un campo e.m. Generalizzazione delle equazioni di Eulero-Lagrange al caso continuo.
Lagrangiana per il campo e.m. libero e in presenza di sorgenti. Equazioni di Eulero-Lagrange ed
equazioni di Maxwell omogenee e non omogenee. Conservazione della corrente.
.