Poligoni - Salesiani Bra

Poligoni
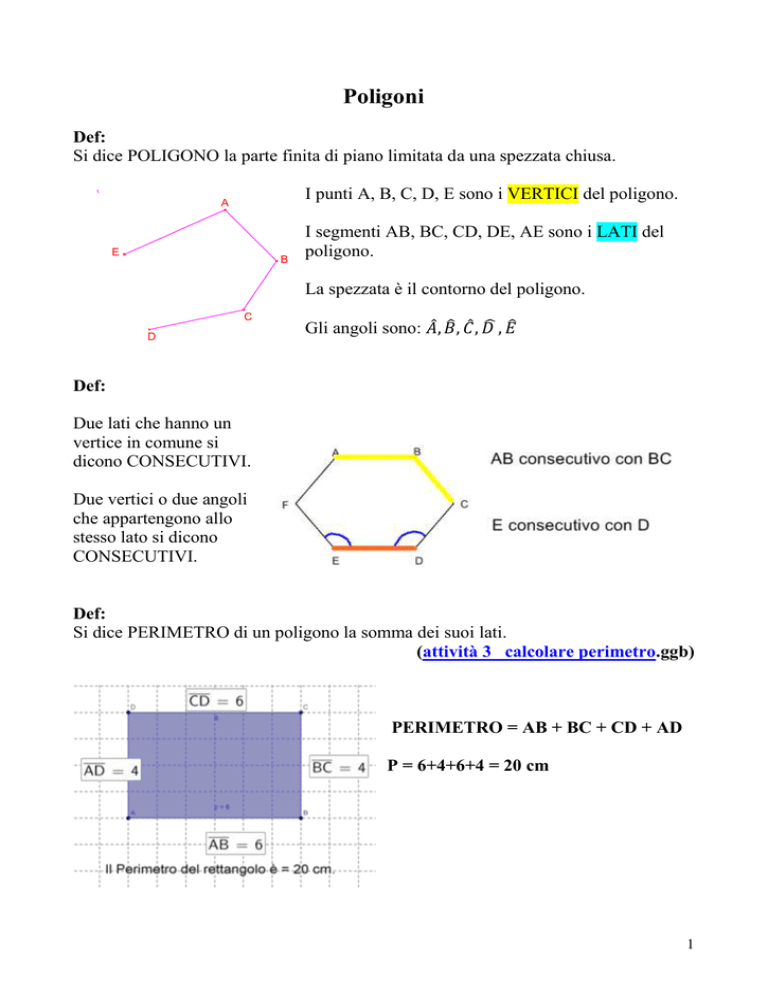
Def:
Si dice POLIGONO la parte finita di piano limitata da una spezzata chiusa.
I punti A, B, C, D, E sono i VERTICI del poligono.
A
E
B
I segmenti AB, BC, CD, DE, AE sono i LATI del
poligono.
La spezzata è il contorno del poligono.
C
D
Gli angoli sono: 𝐴̂, 𝐵̂, 𝐶̂ , 𝐷̂ , 𝐸̂
Def:
Due lati che hanno un
vertice in comune si
dicono CONSECUTIVI.
Due vertici o due angoli
che appartengono allo
stesso lato si dicono
CONSECUTIVI.
Def:
Si dice PERIMETRO di un poligono la somma dei suoi lati.
(attività 3_ calcolare perimetro.ggb)
PERIMETRO = AB + BC + CD + AD
P = 6+4+6+4 = 20 cm
1
Proprietà:
Un poligono si dice CONVESSO se si trova tutto in uno stesso semipiano rispetto a
ciascuna delle rette cui appartiene un suo lato;
si dice CONCAVO se è attraversato da una o più rette alle quali appartiene un suo
lato.
(attività 3_ poligoni convessi_concavi.ggb)
Def:
Si dice ANGOLO INTERNO di un poligono ciascun angolo formato da due lati
consecutivi; si dice ANGOLO ESTERNO ogni angolo adiacente ad un angolo interno
di un poligono.
OSSERVAZIONE:
1. l’angolo esterno è attraversato
dai prolungamenti dei lati che lo
compongono;
2. angolo interno più angolo
esterno sono uguali ad un angolo
piatto (180º)  SUPPLEMENTARI
2
DENOMINAZIONE DEI POLIGONI
Proprietà:
Un poligono ha almeno 3 lati, 3 angoli e 3 vertici.
Un poligono prende il nome del numero dei suoi lati o dei suoi angoli.
 Il poligono con 3 lati, 3 angoli e 3 vertici, prende il nome di TRIANGOLO.
 Il poligono con 4 lati, 4 angoli e 4 vertici, prende il nome di QUADRILATERO.
 Il poligono con 5 lati, 5 angoli e 5 vertici, prende il nome di PENTAGONO.
 Il poligono con 6 lati, 6 angoli e 6 vertici, prende il nome di ESAGONO.
 Il poligono con 7 lati, 7 angoli e 7 vertici, prende il nome di ETTAGONO.
3
 Il poligono con 8 lati, 8 angoli e 8 vertici, prende il nome di OTTAGONO.
Def:
Un poligono si dice EQUILATERO se ha tutti i LATI CONGRUENTI.
Esempio:
ROMBO
Costruzione:
 si disegna una diagonale (segmento)
 si trova il punto medio M
 si traccia una retta perpendicolare al segmento nel punto
medio (cioè l’ASSE del segmento)
 si prende un punto sull’asse e si trova il suo simmetrico
 si trova la diagonale maggiore
Def:
Un poligono si dice EQUIANGOLO se ha tutti gli ANGOLI CONGRUENTI.
Esempio:
RETTANGOLO
Def:
Un poligono si dice REGOLARE se è equilatero ed equiangolo e cioè se ha tutti i lati
e tutti gli angoli congruenti.
Es:
Il ROMBO non è regolare, perché ha i lati uguali , ma gli angoli no.
Il RETTANGOLO non è regolare, perché ha gli angoli uguali, ma i lati no.
Il QUADRATO è REGOLARE.
4
Per tutti i poligoni che sono regolari, nel nome si aggiunge la parola “REGOLARE”:
esempio l’ ESAGONO REGOLARE, il PENTAGONO REGOLARE,
l’OTTAGONO REGOLARE….
 PENTAGONO REGOLARE
(attività 3_ poligoni regolari.ggb)
Proprietà:
Ciascun lato di un poligono è minore della somma di tutti gli altri lati.
(attività 3_ disuguaglianza triangolare.ggb)
Def:
Si dice DIAGONALE di un poligono ogni
segmento che unisce due suoi vertici non
consecutivi.
Regola:
per calcolare il numero delle diagonali di un
poligono si applica la seguente formula
d
n  (n  3)
2
n = numero lati
5
TRIANGOLO  n = 3
d
QUADRILATERO  n = 4
3  (3  3)
 3 0 : 2  0  d = 0
2
d
4  (4  3)
 4 1 : 2  4 : 2  2  d = 2
2
5  (5  3)
 5  2 : 2  10 : 2  5  d = 5
PENTAGONO  n = 5
2
6  (6  3)
d

 (6  3) : 2  18 : 2  9  d = 9
ESAGONO  n = 6
2
7  (7  3)
d

 (7  4) : 2  28 : 2  14  d = 14
ETTAGONO  n = 7
2
d
Regola:
per calcolare il numero delle diagonali uscenti da un vertice di un poligono si applica
la seguente formula:
𝑛−3
n = numero dei lati
Teorema n. 1:
la somma degli angoli interni di un triangolo è uguale a
180 0 .
𝛼 + 𝛽 + 𝛾 = 1800
6
Dimostrazione:
Th:
𝐴̂ + 𝐵̂ + 𝐶̂ = 1800
Si conduce la parallela ad AB per il vertice C: DE // AB
Si considera AB // DE e come trasversale AC, allora:
̂ perché alterni interni
𝐴̂ ≅ 𝐷
Si considera AB // DE e come trasversale BC, allora:
𝐵̂ ≅ 𝐹̂ perché alterni interni
 dal disegno si vede che:
̂ + 𝐶̂ + 𝐹̂ = 1800
𝐷
Sostituendo nella formula quanto trovato si ottiene:
𝐴̂ + 𝐶̂ + 𝐵̂ = 1800
c.v.d.
7
Teorema n. 2:
in ogni triangolo, un angolo esterno è congruente alla somma dei due angoli interni
ad esso non adiacenti.
𝐶𝐵̂𝐷 = 𝛼 + 𝛾
Dimostrazione:
Dal Teorema precedente:
𝐴̂ + 𝐵̂ + 𝐶̂ = 1800
Sappiamo che un angolo esterno più un angolo interno fanno 1800 :
̂ = 1800
𝐵̂ + 𝐷
Si prolunga il lato AB dalla parte del vertice B, e si considera l’angolo esterno CBˆ D ,
esso è supplementare del suo angolo interno ABˆ C , quindi ABˆ C + CBˆ D = 180 0
Ma dal teorema della somma degli angoli interni si sa che
ABˆ C + BCˆ A + CAˆ B = 180 0 e dalla formula precedente:
ABˆ C + CBˆ D = 180 0 , quindi CBˆ D = BCˆ A + CAˆ B
Teorema n. 3:
8
la somma degli angoli interni di un poligono di n lati è:
S i  (n  2)  180 0
n = numero dei lati del poligono.
Es:
TRIANGOLO: 𝑆𝑖 = (𝑛 − 2) ∙ 1800 = (3 − 2) ∙ 1800 = 1 ∙ 1800 = 1800
QUADRILATERI: 𝑆𝑖 = (𝑛 − 2) ∙ 1800 = (4 − 2) ∙ 1800 = 2 ∙ 1800 = 3600
PENTAGONO: 𝑆𝑖 = (𝑛 − 2) ∙ 1800 = (5 − 2) ∙ 1800 = 3 ∙ 1800 = 5400
ESAGONO: 𝑆𝑖 = (𝑛 − 2) ∙ 1800 = (6 − 2) ∙ 1800 = 4 ∙ 1800 = 7200
Teorema n. 4 :
la somma degli angoli esterni di un poligono qualsiasi è:
S e  3600 ( qualunque sia il numero dei lati)
Disegno
Teorema n. 5:
la somma degli angoli interni e degli angoli esterni di un poligono di n lati è:
𝑆𝑡 = 𝑛 ∙ 1800
𝑆𝑡 = somma totale angoli interni e esterni
TRIANGOLO: 𝑆𝑡 = 𝑛 ∙ 1800 = 3 ∙ 1800 = 5400
QUADRILATERI: 𝑆𝑡 = 𝑛 ∙ 1800 = 4 ∙ 1800 = 7200
PENTAGONO: 𝑆𝑡 = 𝑛 ∙ 1800 = 5 ∙ 1800 = 9000
(dimostrazione solo da leggere e capire sul libro pag. 138)
RIEPILOGO:
SOMMA ANGOLI INTERNI
TRIANGOLO
𝑺𝒊 = 𝟏𝟖𝟎𝟎
9
TRIANGOLO:ANGOLO
ESTERNO UGUALE SOMMA
ANGOLI INTERNI NON
ADIACENTI
𝐶𝐵̂𝐷 = 𝛼 + 𝛾
SOMMA ANGOLI INTERNI
𝑺𝒊 = (𝒏 − 𝟐) ∙ 𝟏𝟖𝟎𝟎
SOMMA ANGOLI ESTERNI
𝑺𝒆 = 𝟑𝟔𝟎𝟎
SOMMA TOTALE ANGOLI
(interni più esterni)
𝑺𝒕 = 𝒏 ∙ 𝟏𝟖𝟎𝟎
10