CONTROLLO INDUSTRIALE
MODELLO DI UN PENDOLO INVERSO DA LABORATORIO
Prof. Lalo Magni
Descrizione parametri modello
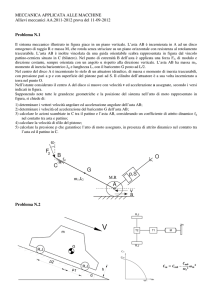
Figure 1: Schema semplificato di un pendolo inverso da laboratorio
In Figura 1 è rappresentato lo schema meccanico semplificato del processo. Per semplicità di realizzazione sono
state fatte le seguenti ipotesi:
• il carrello è descrivibile come un corpo puntiforme di massa M concentrata nel baricentro;
• la massa m dell’asta è concentrata nel baricentro;
• non sono modellizate le forze d’attrito.
Nel seguito si utilizzerà la seguente simbologia.
• M : massa del carrello (0.455 kg).
• m: massa dell’asta (0.21 kg).
• θ: angolo formato dall’asta con la verticale passante per il baricentro del carrello ([rad]).
• ω: velocità angolare dell’asta ([rad/s]).
• x: posizione del carrello ([m]).
• v: velocità del carrello ([m/s]).
• F : forza applicata al carrello ([N ]).
• l: metà della lunghezza dell’asta (0.305 m).
• A: baricentro dell’asta.
• B: baricentro del carrello.
1
Equazioni del moto
Definiamo le relazioni cinematiche tra le grandezze x, v, θ, ω.
Siano:
• aA : vettore accelerazione del punto A;
• aB : vettore accelerazione del punto B.
Applicando il teorema di Rivals:
aA = aB + aAB
(1)
in cui la componente aAB rappresenta l’accelerazione di A rispetto a B. Si scompone dunque il vettore aAB in
due componenti, la prima lungo la congiungente tra A e B (aABn ) e la seconda lungo la retta perpendicolare ad essa
(aABt ). I moduli dei vettori sono definiti come segue:
aB =
dv
dω
aABn = ω 2 l aABt =
l.
dt
dt
Dal grafico riportato in Figura 2, attraverso semplici calcoli trigonometrici, si possono determinare le relazioni che
legano le componenti lungo gli assi X e Y del vettore aA con le variabili di stato x, v, theta e ω.
Figure 2: Somma vettoriale (1)
aAX =
dω
dv
− ω 2 l sin θ +
l cos θ
dt
dt
aAY = ω 2 l cos θ +
dω
l sin θ
dt
(2)
(3)
L’equazione di equilibrio alla traslazione orizzontale è:
F −M
dv
= maAX
dt
sostituendo in (2) si ottiene:
dω
dω
− mω 2 l sin θ + m l cos θ = F.
dt
dt
Si passa ora a considerare l’equazione di equilibrio di rotazione dell’asta attorno al punto B:
(M + m)
(4)
maAX l cos θ + maAY lsinθ − mgl sin θ = 0
sostituendo (2) e (3)
dv
dω
= g sin θ −
cos θ.
(5)
dt
dt
Le equazioni (4) e (5) descrivono completamente il sistema meccanico. Riscriviamo le equazioni nella forma di
sistema di equazioni nonlineari nelle variabili di stato x, v, θ, ω:
l
ẋ =v
1
(ml2 ω 2 sin θ − mg cos θ sin θ + F )
M + m − m cos2 θ
θ̇ =ω
cos θ
1
(mg cos θ sin θ − ml2 ω 2 sin θ − F ))
ω̇ = (g sin θ +
l
M + m − m cos2 θ
v̇ =
2
Modello del motore
L’attuatore utilizzato è un motore in corrente continua.
I parametri del modello sono i seguenti.
• km : costante di coppia (0.00767
N
A)
• kg : rapporto di trasmissione (3.7)
• ρm : rendimento del motore (0.87)
• ρr : rendimento del riduttore (0.9)
• Ra : resistenza di armatura (2.6 Ω)
• r: raggio della ruota (0.0064 m)
• V : tensione applicata al motore ([V ])
Il modello del motore in corrente continua in cui si esplicita la forza F è il seguente:
km kg ρr
F =V
−
Ra r
km kg ρr
r
La tensione V applicata al motore è l’ingresso del sistema.
Variabili di stato, di controllo e di uscita
x1 = x
x2 = v
x3 = θ
x4 = ω
u=V
y1 = x
y2 = θ
3
2
1
v.
Ra ρm