Università degli studi di Trieste
Facoltà di Ingegneria
Laurea in Ingegneria dell’Informazione
a.a. 2001/2002
APPUNTI del CORSO di ELETTROTECNICA
Introduzione al Trasformatore Reale
docente: Stefano Pastore
1
Descrizione del trasformatore
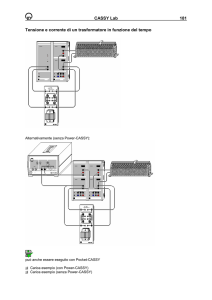
Consideriamo lo schema di principio di un trasformatore (vedi Fig. 1). E’ costituito da due
avvolgimenti (il primario e il secondario) avvolti su un nucleo laminato di materiale ferromagnetico. Il primario è alimentato con una tensione sinusoidale pari a V1 = VA1 − VB1 ,
mentre il secondario alimenta un carico generico zc tramite la tensione V2 = VA2 − VB2 .
Supponiamo di suddivedere le linee di flusso magnetico in tre classi fondamentali:
1. linee di flusso che si richiudono interamente sul ferro, disposte prevalentemente sulla
linea mediana del circuito magnetico,
2. linee di flusso che si richiudono in aria concatenandosi con il solo primario,
3. linee di flusso che si richiudono in aria concatenandosi con il solo secondario.
Le linee di flusso di tipo 1, concatenate con entrambi i circuiti, costituiscono il flusso
principale φ della macchina. Tale flusso è costante in ogni sezione S della macchina, e
come tale si concatena con le N1 spire del primario e le N2 spire del secondario.
I flussi di tipo 2 e 3 danno origine ai flussi φd1 e φd2 , che si chiamano, rispettivamente,
flusso di autoinduzione di dispersione primario e flusso di autoinduzione di dispersione
secondario. Supponendo che tali flussi operino in regime di linearità e quindi siano proporzionali alle correnti, si ha:
φd1 = Ld1 i1
(1)
φd2 = Ld2 i2
1
Fig. 1: Schema di principio di un trasformatore.
dove Ld1 è il coefficiente di autoinduzione di dispersione primario e Ld2 è il coefficiente di
autoinduzione di dispersione secondario. Notiamo come questi flussi dispersi siano localizzati parzialmente in aria, materiale che ha una elevata riluttanza. Ciò rende trascurabili
le cadute di tensione magnetica nel ferro, e riduce gli effetti di una eventuale saturazione
del campo. E’ allora giustificato l’impiego di relazioni lineari nelle eq. (1).
Come conseguenza, ne risulta che i flussi φc1 e φc2 complessivamente concatenati con,
rispettivamente, il primario e il secondario sono dati da:
φc1 = N1 φ + φd1 = N1 φ + Ld1 i1
φc2 = N2 φ + φd2 = N1 φ + Ld2 i2
2
(2)
Equazioni interne
Supponendo che il materiale del nucleo ferromagnetico si comporti linearmente, possiamo
utilizzare la legge di Hopkinson al circuito magnetico interessato al flusso principale φ,
per cui si ha:
(3)
N 1 i1 + N 2 i2 = R φ
dove R è la riluttanza del del tubo di flusso di φ, con buona approssimazione coincidente
con il nucleo del trasformatore. L’ipotesi ora fatta è basata sulla linearizzazione della curva
di isteresi del materiale ferromagnetico impiegato. Non entriamo in ulteriori dettagli, ma
diamo per scontato che ciò sia possibile. Aggiungiamo solo che la permeabilità magnetica
µ, presente nella formula R = l/µS, deve essere calcolata considerando la pendenza della
retta che congiunge l’origine degli assi al punto di lavoro sulla curva di isteresi, punto
determinato dalla tensione di alimentazione del primario.
L’ipotesi di linearità ci permette, inoltre, di scrivere le cadute sugli avvolgimenti dovute
al flusso completo e ai flussi concatenati. Ricordando la legge di Faraday, si ha:
dφc1
dφ
d i1
= N1
+ Ld1
v1φ =
dt
dt
dt
(4)
dφ
d i2
dφc2
v2φ =
= N2
+ Ld2
dt
dt
dt
2
da cui le due equazioni interne del trasformatore sono, tenuto conto degli opportuni segni:
v1 − v1φ = R1 i1
(5)
−v2 − v2φ = R2 i2
dove R1 e R2 rappresentano le resistenze degli avvolgimenti, rispettivamente, del primario
e del secondario.
Se il carico zc è lineare, è pure lineare tutto il sistema trasformatore carico, e se
l’alimentazione è sinusoidale a frequenza angolare ω, si può passare ai fasori per scrivere le equazioni interne del trasformatore. Trasformando e raccogliendo le eq. (3), (4) e
(5), si ottiene:
V1 − jωN1 Φ − jωLd1 I1 = R1 I1
−jωN2 Φ − jωLd2 I2 = R2 I2 + V2
(6)
N 1 I1 + N2 I2 = R φ
Definendo le reattanze di dispersione primaria e secondaria:
Xd1 = ω Ld1
Xd2 = ω Ld2
le equazioni interne (6) diventano:
V1 = (R1 + j Xd1 ) I1 + jωN1 Φ
0 = (R2 + j Xd2 ) I2 + jωN2 Φ + V2
N 1 I1 + N 2 I2 = R φ
(7)
(8)
Queste equazioni descrivono il funzionamento del trasformatore con qualsiasi carico.
3
Equazioni esterne
Le eq. (8) costituiscono un sistema di 3 equazioni complesse in 5 variabili complesse
V1 , V2 , I1 , I2 , Φ, vale a dire in 10 variabili reali, che si riducono a 9 fissando arbitrariamente la fase di una delle grandezze. Le 3 equazioni complesse corrispondono a 6 equazioni
reali, in quanto ogni equazione costituosce un vincolo per la parte reale delle variabili e
un vincolo per la parte immaginaria. Rimangono perciò da fissare aancora 3 gradi di
libertà per la completa ed univoca soluzione del problema, cioè per la determinazione
delle 5 variabili complesse. Le 3 condizioni che dobbiamo ancora imporre costituiscono le
equazioni di collegamento con l’esterno, o equazioni esterne del trasformatore.
Esse sono costituite da:
V1 = V1s
(9)
V2 = zc I2
Dove la prima equazione riguarda solo il modulo della tensione di alimentazione, in quanto
la sua fase è già stata presa come riferimento.
Complessivamente, abbiamo ora nove equazioni reali in 9 incognite reali: il problema
trasformatore è ora risolvibile.
3
4
Sistema completo approssimato
Un trasformatore progettato correttamente presenta delle reattanze di dispersione e delle
resistenze interne piuttosto modeste, per limitare le cadute su tali componenti a pochi
punti percentuali della caduta complessiva. Trascurando perciò tali cadute, si ottiene
dalle prime due equazioni delle (8):
V1 jωN1 Φ
(10)
−V2 = jωN2 Φ
da cui si deduce che:
N1
V1
=
V2
N2
(11)
equazione fondamentale del trasformatore, dove il rapporto N1 /N2 è chiamato rapporto
spire o rapporto di trasformazione. Analogamente, trascurando nella terza equazione del
sistema (8) il termine R φ, normalmente modesto di entità, si ottiene:
I1
N2
=
I2
N1
(12)
Pa1 = V1 I1 = V2 I2 = Pa2
(13)
Una conseguenza diretta è che:
dove i moduli delle tensioni e delle correnti sono intesi come valori efficaci. Quindi le
potenze apparenti in ingresso (misurate in [VA]) al primario del trasformatore ed in uscita
dal secondario sono uguali, avendo però cambiato secondo il rapporto spire il valore della
tensione e inversamente quello della corrente. la potenza attiva effettiva sarà determinata
dal carico che aggiungerà il fattore di potenza alla tensione e alla corrente in uscita.
Il sistema totale approssimato delle equazioni interne ed esterne si può riassumere come:
V1 jωN1 Φ
−V2 = jωN2 Φ
N 1 I1 + N 2 I2 = 0
(14)
V1 = V1s
V2 = zc I2
Le equazioni possono essere risolte in sequenza, partendo dalla tensione di alimentazione
V1s , la cui fase può essere presa come riferimento, da cui si trova il flusso Φ, La tensione
V2 , la corrente I2 ed infine la corrente I1 .
4