Cognome___________________Nome_________________
VERIFICA DELLE COMPETENZE DI MATEMATICA - Classe 1CL
Prima Prova Esperta – Febbraio 2012
Prima di cominciare leggi bene queste istruzioni
A - Come e dove rispondere
In questa prova dovrai rispondere a domande e svolgere del lavoro grafico.
Rispondi alle domande su un foglio protocollo a quadretti e svolgi gli esercizi grafici nel, negli
appositi spazi che sono all’interno del testo.
B - Cosa fare se ci sono cose che non capisci
Il testo del compito è stato scritto cercando di usare parole semplici e i termini che dovresti avere
imparato, dal libro o dalla lezione, in questo primo periodo.
Potrebbero esserci comunque parole o espressioni che non conosci o non capisci. Prima di provare a
rispondere alle domande sarà meglio che tu cerchi di chiarire i punti oscuri e potrai:
- rileggere con più attenzione e calma le domande;
- cercare il significato in un dizionario, che sarà a disposizione in aula.
Se ci sono parole o espressioni che NON capisci annotale nella penultima pagina
Ad ogni domanda corrisponde uno spazio dove poter scrivere, diviso in due colonne.
Nella colonna di sinistra scrivi le parole che NON
capisci,
Nella colonna di destra scrivi il significato che credi
che esse abbiano, se a un certo punto ti sembra di
averle capite.
Foglio 1 di 7
Cognome___________________Nome_________________
Prima parte
1 – Piante in giardino e giardini in
pianta
Premessa (leggi attentamente)
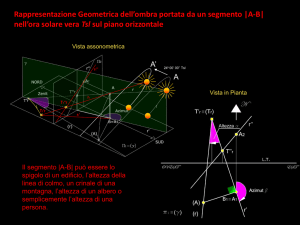
Nella immagine qui accanto sono
riprodotte la fotografia di un giardino e
la sua pianta.
La forma può apparire a prima vista di
una certa complessità, anche se ha una
evidente simmetria.
Forme complesse possono, però, essere
generate da forme semplici, con
procedimenti di “somma” o
“sottrazione”.
Qui sotto vedi, per esempio, come una
figura irregolare possa essere vista
come la combinazione di due figure
semplici:
Fig 2 – la figura complessa asimmetrica di sinistra
è quella che si otterrebbe coprendo un
quadrato con un cerchio bianco
Si potrebbe dire che la figura è stata
ottenuta “sottraendo” un cerchio a un
quadrato.
Fig. 1 – Una foto prospettica del giardino e il suo disegno in
pianta. Non si hanno informazioni sulle lunghezze ma
si sa in che rapporto fra gli elementi di base
Seguendo questa idea:
a) Identifica i diversi tipi di figure complesse che compongono la pianta e, a questo scopo:
- assegna un numero a ogni tipo di forma
- scrivi su ogni elemento della figura il numero che corrisponde al suo tipo
b) Elenca le figure di base che sono sufficienti a generare la pianta
c) Spiega con quale sequenza di operazioni di “somma”
e “sottrazione” di figure di base può essere generata
la figura centrale (la parte nera nella figura qui
accanto)
Foglio 2 di 7
Cognome___________________Nome_________________
d) Nella fig. 1 NON sono indicate misure in centimetri ma sono indicate le proporzioni fra
alcuni elementi essenziali del disegno: si capisce, per esempio che il raggio del cerchio
centrale,
L
, è la metà della misura di riferimento L.
2
Usando per L la misura del segmento raffigurato qui:
L = ____
realizza con squadra e compasso la pianta, mostrando chiaramente come riesci a
mantenere le proporzioni corrette.
Nota Bene: non devi usare la misura in centimetri ma sfruttare la congruenza fra
segmenti
Foglio 3 di 7
Cognome___________________Nome_________________
Seconda parte
2 – Se sai allora sai spiegare
a) Immagina di dover scrivere una parte di un libro di Geometria in cui si spiega come trovare
il punto medio di un segmento.
Il tuo lavoro deve essere organizzato in questo modo:
a1) fai una breve introduzione in cui dirai cosa stai per spiegare;
a2) spiega, con parole e con disegni, la procedura da seguire (cioè tutte le cose che
bisogna fare;
Spazio per i disegni della domanda 2.a2
b) Non è possibile giustificare questo metodo usando solo i teoremi sui triangoli che hai
studiato fino ad ora: servono altre idee e teoremi che ancora non conosci. e ti è stato
chiesto di fidarti.
C’è, però, qualcosa che può essere dimostrato.
Infatti, per trovare il punto medio si traccia, in pratica, anche un segmento perpendicolare
al segmento da dividere in due; questo segmento perpendicolare passa proprio per il punto
medio. Questo segmento appartiene a una retta che si chiama asse del segmento iniziale.
b1) spiega in modo rigorosamente logico, attraverso le tue conoscenze sui teoremi e i
criteri che riguardano i triangoli, il motivo per cui il segmento è certamente
perpendicolare.
(suggerimento: ripensa a cosa vuol dire “perpendicolari” e ricorda che un angolo piatto è
congruente alla somma di due angoli retti)
b2) Il concetto di asse di un segmento è stato detto qualche riga sopra, alla conclusione di
un discorso in cui non era l’argomento principale.
Scrivi tu, ora, una definizione breve e chiara per “asse di un segmento”.
Foglio 4 di 7
Cognome___________________Nome_________________
3 – Se sai allora sai fare
a) Con il metodo che hai descritto prima puoi disegnare solo segmenti perpendicolari che
passano per il punto medio. Spesso però bisogna tracciare segmenti perpendicolari che
passano per altri punti.
Nella Fig. 1a (Foglio 5) vedi un segmento, chiamato
a e un punto, P, che non gli appartiene.
Nella Fig. 1b vedi il primo passaggio grafico per tracciare un segmento, che chiamerai b,
che parta da P e cada perpendicolarmente al segmento a.
a1) Disegna il segmento b
Spazio per la domanda 3.a1 – Finisci la costruzione richiesta sopra la Fig. 1b
b) Il primo passaggio, illustrato nella Fig. 1b, permette di identificare un triangolo
b1) di che tipo di triangolo si tratta?
b2) spiega, facendo riferimento agli opportuni teoremi, il motivo per cui il segmento b è
certamente perpendicolare al segmento a.
c) Nella fig. 2 (Foglio 5) è rappresentato un segmento di estremi A e B. Questo segmento è la
base di un rettangolo la cui altezza deve essere la metà della base.
c1) Spiega che strategia userai per determinare l’altezza usando solo la riga e il compasso.
c2) disegna il rettangolo, usando solo riga e compasso.
Foglio 5 di 7
Cognome___________________Nome_________________
4 – Dimostrazione
a1) Disegna un segmento AC. Il segmento, come sai, appartiene a una retta che divide il piano
in due parti uguali.
Da una parte disegna un triangolo isoscele con base AC e vertice B e dall’altra un altro
triangolo isoscele con vertice D.
Traccia BD
a2) Dimostra che BD è bisettrice dell’angolo ABC
Foglio 6 di 7
Parole che non conosco
Parole non capite
Significato attribuito
Domanda 1
a
b
c
d
Domanda 2
a
a1
a2
b
b1
b2
Domanda 3
a
a1
b
b1
b2
C
c1
c2
Foglio 7 di 7