L2.mat, punto di formazione per matematica e fisica (cerca con Google maps)
Problema sulla circonferenza
In una circonferenza di raggio r sono fissate due corde tra loro parallele e situate dalla stessa parte
rispetto al centro della circonferenza. Sapendo che le misure delle due corde sono 60cm e 48cm e che la
loro distanza è 6cm, determinare:
1. il raggio della circonferenza;
2. il perimetro del trapezio avente per basi le due corde;
3. l’area del settore circolare il cui arco è sotteso dalla corda maggiore e che contiene il trapezio
suddetto.
Elaborazioni
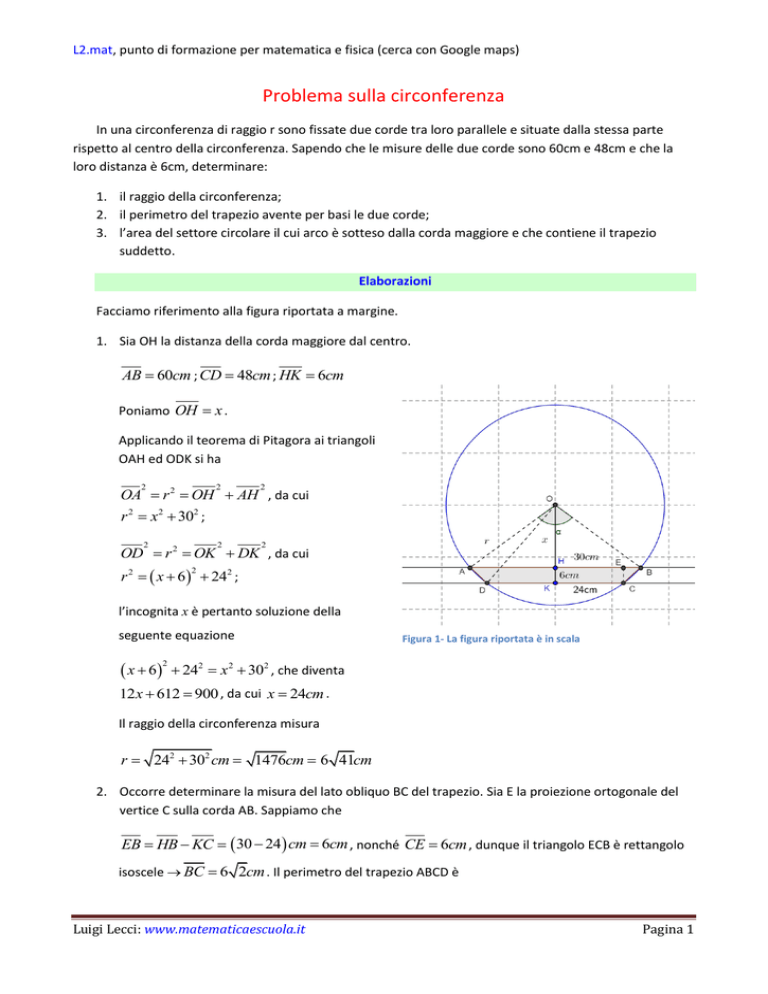
Facciamo riferimento alla figura riportata a margine.
1. Sia OH la distanza della corda maggiore dal centro.
AB 60cm ; CD 48cm ; HK 6cm
Poniamo OH x .
Applicando il teorema di Pitagora ai triangoli
OAH ed ODK si ha
2
2
2
2
2
OA r 2 OH AH , da cui
r 2 x2 302 ;
2
OD r 2 OK DK , da cui
r 2 x 6 242 ;
2
l’incognita x è pertanto soluzione della
seguente equazione
x 6
2
Figura 1- La figura riportata è in scala
242 x 2 302 , che diventa
12 x 612 900 , da cui x 24cm .
Il raggio della circonferenza misura
r 242 302 cm 1476cm 6 41cm
2. Occorre determinare la misura del lato obliquo BC del trapezio. Sia E la proiezione ortogonale del
vertice C sulla corda AB. Sappiamo che
EB HB KC 30 24 cm 6cm , nonché CE 6cm , dunque il triangolo ECB è rettangolo
isoscele BC 6 2cm . Il perimetro del trapezio ABCD è
Luigi Lecci: www.matematicaescuola.it
Pagina 1
L2.mat, punto di formazione per matematica e fisica (cerca con Google maps)
2 p ABCD AB 2BC CD 12 9 2 cm
3. Sia l’angolo al centro del settore in oggetto. L’area S del settore si ottiene con la seguente
formula
S
1 2
r , con espresso in radianti.
2
Osserviamo che
30cm
5
5
HB
, da cui 2arcsen
sen
.
41
2 OB 6 41cm
41
L’area del settore è
S
2
1
5
5
6 41 2arcsen
1476 arcsen
2
41
41
Luigi Lecci: www.matematicaescuola.it
1476 0,896055 1322,5777 cm2.
Pagina 2












