Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE
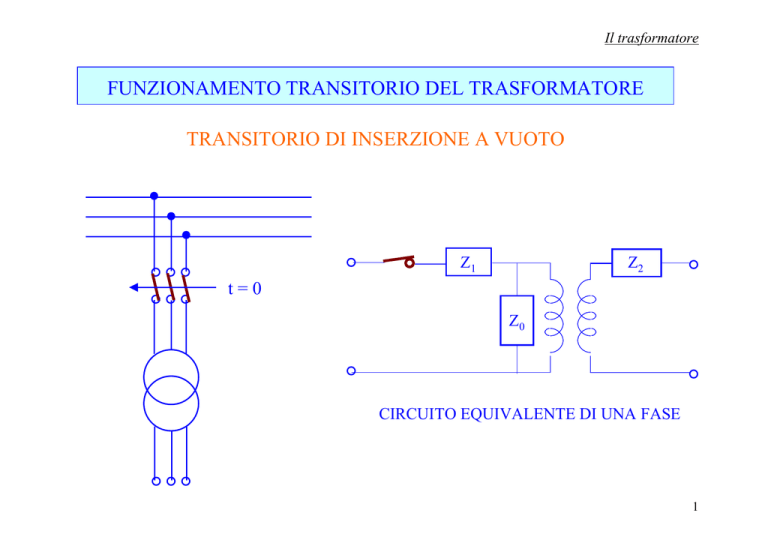
TRANSITORIO DI INSERZIONE A VUOTO
Z1
Z2
t=0
Z0
CIRCUITO EQUIVALENTE DI UNA FASE
1
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
Per lo studio del transitorio si introduce la NON LINEARITÀ nel legame flussicorrenti.
Le equazioni di funzionamento sono:
dΨ
[ v ] = [ R ][i ] +
d t
ove Ψ = Ψ(i) è una funzione NON LINEARE.
La risoluzione di questo sistema di equazioni differenziali non lineari può essere
condotta su calcolatore numerico o su calcolatore analogico.
Una soluzione approssimata e quindi una interpretazione approssimata del
problema è ottenibile nel seguente modo:
• si introduce l’ipotesi di LINEARITÀ;
• si trascura l’induttanza di dispersione primaria:
L 1 = L A1 + L m 1
;
• la corrente secondaria è nulla.
2
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
Il sistema di equazioni si riduce alla sola equazione primaria:
v 1 = R 1i1 + L m 1
d i1
dt
v1 = VM s i n ω t
i 1 = i R E G IM E + i O M O G E N E A = I M sin ( ω t − ϕ ) + A e − t
T
I valori delle correnti del transitorio sono sensibilmente influenzati dal valore
della tensione v1 all’istante di chiusura dell’interruttore:
3
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
Istante iniziale:
ωt = 0
i1 = 0
A = − I M sin ( − ϕ )
i 1 = I M sin ( ω t − ϕ ) + I M sin ϕ e − t
Istante iniziale:
ωt = π/2
A = − IM
T
i1 = 0
π
sin − ϕ
2
i 1 = I M sin ( ω t − ϕ ) − I M
π
sin − ϕ e − t
2
T
Si noti che, per ϕ = π/2, cioè R1 ≈ 0, la corrente di regime si stabilisce
istantaneamente partendo da valore nullo.
4
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
In presenza di transitorio, la corrente i1 istantanea, dopo circa mezzo periodo,
raggiunge un valore doppio di quello di regime.
Caso di ϕ = π/2
(ωt)iniziale = 0
5
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
INTERPRETAZIONE
SATURAZIONE
DEL
FENOMENO
INTRODUCENDO
LA
Se si tiene conto del fenomeno di saturazione dei materiali magnetici,
all’aumentare della corrente diminuisce il valore dell’induttanza magnetizzante
Lm1 e si innesca un fenomeno caratterizzato da un forte aumento di corrente e da
un accorciamento del transitorio (T = Lm1/R1).
L’aumento della corrente è ancora più sensibile se si tiene conto dei fenomeni di
isteresi e in particolare della presenza di un flusso residuo nel nucleo all’istante
iniziale. In questo caso, l’induttanza magnetizzante Lm1 raggiunge valori molto
bassi e la corrente di inserzione può raggiungere valori pari a 10-20 volte la
corrente nominale del trasformatore (e quindi valori pari anche a 1000 volte la
corrente a vuoto con tensione nominale I0n).
Si noti che il flusso RESIDUO esiste in modo rilevante quando l’apertura del
collegamento tra trasformatore e linea (antecedente alla successiva inserzione)
avviene con flusso prossimo al valore di saturazione.
6
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE A VUOTO
N.B.: Il fenomeno del transitorio di inserzione si smorza per effetto dei
fenomeni dissipativi ed evolve verso il funzionamento di regime a vuoto che è
stato già oggetto di studio.
7
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE
TRANSITORIO DI CORTO CIRCUITO
Zcc
t=0
i
v
CIRCUITO EQUIVALENTE IN
CORTO CIRCUITO A REGIME
8
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE in corto circuito
A partire da una qualsiasi condizione di funzionamento (a vuoto o a carico), si
suppone di chiudere il trasformatore su un carico a impedenza nulla.
Il transitorio di corrente è di tipo R-L e il valore di regime è imposto dal valore di
Zcc e dalla tensione applicata.
I fenomeni che interessano sono principalmente due:
• la CORRENTE DI CORTO CIRCUITO PERMANENTE ha importanza ai fini
del riscaldamento. Se ne considera perciò il valore efficace che, a tensione
nominale, è espresso da:
I cc =
Vn
Z cc
• la CORRENTE DI CORTO CIRCUITO TRANSITORIA (ed in particolare il
suo valore nel primo mezzo periodo) ha importanza per gli sforzi meccanici.
9
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE in corto circuito
Nella peggiore condizione possibile (inizio del corto circuito quando la tensione
è nulla) e prescindendo dallo smorzamento della componente transitoria
unidirezionale, si può raggiungere un valore che è circa il doppio della
componente di regime dopo un semiperiodo (2√2Icc).
Tenendo conto dello smorzamento, si può arrivare a valori pari a 2,5 Icc.
10
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE in corto circuito
Gli SFORZI ELETTRODINAMICI sono proporzionali al quadrato della corrente
e, poiché la corrente negli avvolgimenti sono CONTROVERSE, sono sforzi di
repulsione.
Se gli avvolgimenti sono centrati, lo sforzo è radiale.
11
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE in corto circuito
+
.
+
.
Esempio di calcolo dello sforzo
Lo sforzo può essere espresso come derivata, rispetto alla distanza radiale dei
due avvolgimenti (y), dell’energia accumulata nel campo magnetico di
dispersione:
dE
d 1 2 1 2 dL
=
F=
Li = i
dy 2
dy
dy
2
Per
i M A X = 2, 5 I cc
⇒
(ove si può ritenere: L = k y )
2
FM A X = ( 2, 5 ) I cc
2
12
Il trasformatore
FUNZIONAMENTO TRANSITORIO DEL TRASFORMATORE in corto circuito
Si noti che si può dimostrare che, per un trasformatore, vale:
F [ N ] = A n [V A ]
13