F2
30˚
F1
F F
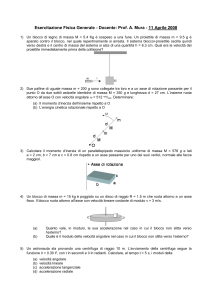
Un blocco di ghiaccio di massa 5,0 Kg è spinto da due forze 1 e 2 , orientate come in figura. Il
modulo di F1 è 20N, quello di F2 è 35N. Il blocco è libero di muoversi senza attrito sul pavimento.
a) Il blocco si muove verso l’alto o soltanto orizzontalmente sul pavimento ?
Bisogna capire se le forze verticali verso l’alto sono maggiori o minori del peso, che è l’unica forza
verticale verso il basso.
F1 y = ...
F2 y = ...
Peso = ...
A questo punto, tenendo conto delle direzioni delle forze, si può dare la risposta A.
b) Il blocco si muove verso destra o verso sinistra ?
c) Qual è la sua accelerazione ?
Scomporre le forze nella loro componente orizzontale, e poi sommarle tenendo conto della loro
direzione. E’ come l’esercizio della scorsa lezione. Poi F = M·a per trovare l’accelerazione.
d) Se si vuole tenere fermo il blocco, quale forza si dovrebbe fare ? In quale direzione ?
La somma delle forze nella direzione orizzontale (la direzione x) deve essere 0. Scrivendo
l’equazione si avrà F3 (la nuova forza) come incognita.
F F
Un blocco di ghiaccio di massa 8,3 Kg è spinto da due forze 1 e 2 , orientate come in figura e di
modulo rispettivamente 50N e 35N. Il blocco è libero di muoversi senza attrito sul pavimento.
F1
F2
25˚
55˚
a) Il blocco si muove verso destra o verso sinistra ?
b) Qual è la sua accelerazione ?
Scomporre le due forze, determinandone la componente orizzontale:
F1x = ...
F2 x = ...
Quale delle due è più grande ? (risposta A)
Determinare la forza complessiva orizzontale, sommando
F1x e F2 x
(attenzione ai segni).
Fx = ...
Dal secondo principio della dinamica
F = m⋅a
determinare l’accelerazione del blocco (risposta B).
Se le due forze sono applicate per un tempo di 12 secondi, calcolare quanto spazio percorre il corpo:
c) nei 12 secondi in cui avviene la spinta
d) nei 10 secondi successivi
Usare le equazioni del moto uniformemente accelerato e del moto uniforme.
Determinare la forza esercitata dal pavimento per sostenere il blocco:
e) durante la spinta
f) al termine della spinta
Si devono scomporre le forze considerandone questa volta la componente verticale. Ricordarsi del
peso.
Al termine della spinta l’unica forza che agisce è il peso.