Disequazioni di 2° grado - Digilander

Appunti di matematica
Disequazioni di secondo grado
Disequazioni di secondo grado
Ogni disequazione di secondo grado può essere ricondotta alla forma normale:
ax 2 + bx + c > 0 con a ≠ 0
(oppure ax 2 + bx + c < 0 , ax 2 + bx + c ≥ 0 , ax 2 + bx + c ≤ 0 )
Nota. Possiamo sempre fare riferimento ai casi in cui il coefficiente a è positivo.
Infatti se a è negativo, basta cambiare segno a tutti i termini e invertire il senso delle
disequazioni.
2
2
(Esempio: − x − 2 x + 3 > 0 è equivalente a x + 2 x − 3 < 0 )
Metodo di risoluzione grafico
Nel metodo grafico si fa ricorso alla parabola.
1) Risolvere l'equazione associata: ax 2 + bx + c = 0 e che, a seconda del segno del ∆,
avrà soluzioni reali (distinte o coincidenti) o nessuna soluzione.
Osservazione. Perché risolvere l'equazione associata? Da un punto di vista geometrico
risolvere un’equazione di secondo grado significa determinare i punti in cui la parabola
interseca l’asse x.
 y = ax 2 + bx + c parabola
⇒ ax 2 + bx + c = 0

asse x
y = 0
Ripasso.Si ricorda che per risolvere una tale equazione si utilizzano le seguenti
formule:
∆ = b 2 − 4ac
−b− ∆
x1 =
2a
x2 =
−b + ∆
2a
Si possono presentare i seguenti tre casi:
▪ ∆>0
▪ ∆=0
▪ ∆<0
si hanno due soluzioni reali e distinte x1 e x2;
si hanno due soluzioni reali e coincidenti x1= x2;
non si hanno soluzioni reali, l’equazione è impossibile.
2) Facciamo un grafico “approssimato” della parabola y = ax 2 + bx + c , tenendo in
considerazione il segno di a. Per “approssimato” si intende che non c'è bisogno di
fare il grafico esatto della parabola, ma solamente evidenziare i suoi eventuali
punti di intersezione con l'asse x e tracciarla con la concavità verso l'alto o verso il
basso, a seconda che a sia positivo o negativo.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
1/8
Appunti di matematica
Disequazioni di secondo grado
La concavità si ricava dal segno del coefficiente del termine di secondo grado, cioè
il segno di a:
- concavità verso l'alto se a > 0,
- concavità verso il basso se a < 0.
La parabola e l’asse x si intersecano in
- due punti x1 e x2 se ∆ > 0 ;
- in un punto x1= x2 se ∆ = 0
- in nessun punto se ∆ < 0 .
Soltanto questi due elementi ci interessano in questo ambito: intersezioni e
concavità.
3) Fatto questo, si potrà risolvere la disequazione assegnata semplicemente
osservando il grafico, rispondendo a una di queste domande.
▪ Se la disequazione data è del tipo ax 2 + bx + c > 0 , la domanda è: per quali valori di x
la parabola sta sopra l'asse x?
▪ Se la disequazione data è del tipo ax 2 + bx + c < 0 , la domanda è: per quali valori di x
la parabola sta sotto l'asse x?
▪ Se la disequazione data è del tipo ax 2 + bx + c ≥ 0 , la domanda è: per quali valori di x
la parabola sta sopra o interseca l'asse x?
▪ Se la disequazione data è del tipo ax 2 + bx + c ≤ 0 , la domanda è: per quali valori di x
la parabola sta sotto o interseca l'asse x?Ecco di seguito le situazioni grafiche che
si possono presentare.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
2/8
Appunti di matematica
Disequazioni di secondo grado
Interpretazione grafica delle disequazioni di secondo grado
ax 2 + bx + c > 0
con a > 0
∆>0
∆=0
∆<0
la soluzione è data dai valori della
x per i quali la parabola sta sopra
l'asse x, cioè, come si vede dalla
figura, dagli intervalli esterni alle
intersezioni tra la parabola e l'asse
x: x<x1 x>x2 .
la soluzione è data da qualsiasi
valore di x, purchè diverso dal
punto di intersezione, x1 :
la soluzione è data da tutto
l'insieme dei numeri Reali.
Infatti, per ogni x la parabola sta
sopra l'asse x, ma in x1 lo
interseca. La disequazione, invece,
ci “chiede” i valori di x per i quali la
parabola è strettamente sopra
l'asse x.
ax 2 + bx + c < 0
∆>0
∆=0
con
a>0
∆<0
la soluzione è data dai i valori di x
per i quali la parabola sta sotto
l'asse x, cioè l' intervallo interno
alle intersezioni: x1 <x<x2
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
3/8
Appunti di matematica
Disequazioni di secondo grado
Vediamo alcuni esempi risolti.
Esempio 1.
▪
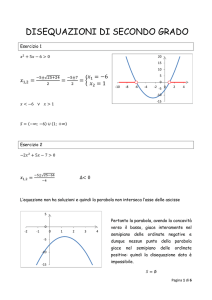
x 2 + 5x − 6 > 0
Svolgimento
2
- Si risolve prima l’equazione associata: x + 5 x − 6 = 0 ; (a=+1; b=+5 ; c=-6)
∆ = b 2 − 4ac = 25 + 24 = 49 > 0
−b− ∆ −5−7
−b+ ∆ −5+7
=
= −6
x2 =
=
= +1
2a
2
2a
2
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x1 = −6 e x 2 = +1
x1 =
- Si osserva l’equazione della parabola y = x 2 + 5 x − 6 ;
a = 1 > 0 ⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purchè passante per i due punti
disegnati e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c > 0 , la domanda è: per quali valori
di x la parabola sta sopra l'asse x?
La disequazione è verificata per x<-6 o x>+1.
Esempio 2.
2
▪ − 6x + x + 1 ≤ 0
Svolgimento
- Si cambia di segno a tutti i termini della disequazioni cambiando anche il verso
della disequazioni + 6 x 2 − x − 1 ≥ 0 .
- Si risolve prima l’equazione associata: + 6 x 2 − x − 1 = 0 ; (a=+6; b=-1 ; c=-1)
∆ = b 2 − 4ac = 1 + 24 = 25 > 0
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
4/8
Appunti di matematica
x1 =
1
− b − ∆ +1 + 5
=
=+
2a
12
2
Disequazioni di secondo grado
x2 =
1
− b + ∆ +1− 5
=
=−
2a
12
3
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x 2 = −
- Si osserva l’equazione della parabola y = 6 x 2 − x − 1 ;
a=6>0
1
1
e x1 = +
3
2
⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purchè passante per i due punti
disegnati e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c ≥ 0 , la domanda è: per quali valori
di x la parabola sta sopra o interseca l'asse x?
1
1
x≤−
x≥+
3
2.
La disequazione è verificata per
o
Esempio 3.
2
▪ 9 x − 30 x + 25 > 0
Svolgimento
2
- Si risolve prima l’equazione associata: 9 x − 30 x + 25 = 0 ; (a=+9; b=-30; c=+25)
∆ = b 2 − 4ac = 900 − 900 = 0 ⇒ due radici reali e coincidenti
x1 = x 2 =
− b ± ∆ + 30 ± 0
5
=
=+
2a
18
3
5
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x1 = x 2 = + .
3
2
- Si osserva l’equazione della parabola y = 9 x − 30 x + 25 ;
a=9>0
⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché passante per l’unico punto
disegnato e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c > 0 , la domanda è: per quali valori
di x la parabola sta sopra l'asse x?
La disequazione è verificata per ogni x ≠ +
5
.
3
Esercizio 4.
2
▪ − 81x + 18 x − 1 ≤ 0
Svolgimento
- Si cambia di segno a tutti i termini della disequazioni cambiando anche il verso
della disequazioni + 81x 2 − 18 x + 1 ≥ 0 .
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
5/8
Appunti di matematica
Disequazioni di secondo grado
- Si risolve prima l’equazione associata: 81x −18x +1 = 0 ; (a=+81; b=-18; c=+1)
2
∆ = b 2 − 4ac = 324 − 324 = 0
x1 =
− b ± ∆ + 18 ± 0
1
=
=+
2a
+ 162
9
1
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x1 = x 2 = + .
9
2
- Si osserva l’equazione della parabola y = +81x − 18 x + 1 ;
a = 81 > 0 ⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché passante per l’unico punto
disegnato e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c ≥ 0 , la domanda è: per quali valori
di x la parabola sta sopra o interseca l’asse x?
La disequazione è verificata per ogni x.
Esempio 5.
2
▪ 4x + 4 x + 1 < 0
Svolgimento
2
- Si risolve prima l’equazione associata: 4 x + 4 x + 1 = 0 ; (a=+4; b=+4; c=+1)
∆ = b − 4ac = 16 − 16 = 0
2
x1 =
−b± ∆ −4±0
1
=
=−
2a
8
2
1
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x1 = x 2 = − .
2
2
- Si osserva l’equazione della parabola y = 4 x + 4 x + 1 ;
a=4>0
⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché passante per l’unico punto
disegnato e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c < 0 , la domanda è: per quali valori
di x la parabola sta sotto l’asse x?
La disequazione non è mai verificata, è impossibile.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
6/8
Appunti di matematica
Disequazioni di secondo grado
Esempio 6.
2
▪ − 9x + 6x − 1 ≥ 0
Svolgimento
- Si cambia di segno a tutti i termini della disequazioni cambiando anche il verso
della disequazioni 9 x 2 − 6 x + 1 ≤ 0 .
- Si risolve prima l’equazione associata: 9 x 2 − 6 x + 1 = 0 ; (a=+9; b=-6; c=+1)
∆ = b 2 − 4ac = 36 − 36 = 0
x1 =
1
−b± ∆ +6±0
=
=+
2a
+ 18
3
1
- Si disegna l’asse x e si fissano su di esso, le due radici trovate x1 = x 2 = + .
3
2
- Si osserva l’equazione della parabola y = 9 x − 6 x + 1 ;
a=9>0
⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché passante per l’unico punto
disegnato e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c ≤ 0 , la domanda è: per quali valori
di x la parabola sta sotto o interseca l’asse x?
La disequazione è verificata solo per
x=+
1
3.
Esempio 7.
▪
x 2 − 2 x + 10 > 0
Svolgimento
2
- Si risolve prima l’equazione associata: x − 2 x + 10 = 0 ; (a=+1; b=-2; c=+10)
∆ = b 2 − 4ac = 4 − 40 = −36 < 0
(l’equazione non ha soluzioni)
- Si disegna l’asse x e non si fissa alcun punto, perché non trovati.
- Si osserva l’equazione della parabola y = x 2 − 2 x + 10 ;
a =1> 0
⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché non intersechi l’asse delle x in
nessun punto e con la concavità rivolta verso l’alto.
- Poichè la disequazione data è del tipo ax 2 + bx + c > 0 , la domanda è: per quali valori
di x la parabola sta sopra l’asse x?
La disequazione è verificata sempre, cioè per ogni x.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
7/8
Appunti di matematica
Disequazioni di secondo grado
Esempio 8.
2
▪ − x + 4x − 5 ≥ 0
Svolgimento
- Si cambia di segno a tutti i termini della disequazioni cambiando anche il verso
della disequazioni x 2 − 4 x + 5 ≤ 0 .
- Si risolve prima l’equazione associata: x 2 − 4 x + 5 = 0 ; (a=+1; b=-4; c=+5)
∆ = b 2 − 4ac = 16 − 20 = −4 < 0
(l’equazione non ha soluzioni)
- Si disegna l’asse x e non si fissa alcun punto, perché non trovati.
- Si osserva l’equazione della parabola y = x 2 − 4 x + 5 ;
a = 1 > 0 ⇒ concavità rivolta verso l ' alto ;
- Si disegna la parabola in modo approssimato purché non intersechi l’asse delle x in
nessun punto e con la concavità rivolta verso l’alto.
- Poiché la disequazione data è del tipo ax 2 + bx + c ≤ 0 , la domanda è: per quali valori
di x la parabola sta sotto o interseca l’asse x?
La disequazione non è mai verificata, cioè è impossibile.
Sitografia
- http://www.itg-rondani.it/dida/Matem/ipermonica/retta_par/parabola/parab09.htm
- http://www.ripmat.it/mate/a/ag/agdca.html
- http://www.ittmazzotti.it/docenti/matematicaestiva2002/AudioLez3/Intr_audio.html
- http://www.webalice.it/rcicero/appunti%20maths/Disequazioni%20SecondoG.doc
- http://www.studenti.it/matematica/biennio/disequazioni_secondogrado.php#ma
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
8/8