Lezione 12 Luglio 2000 – Introduzione alla fisica dello stato solido
1.
Struttura della materia solida
In questo capitolo si affrontano gli aspetti essenziali delle teorie e delle osservazioni sperimentali
rivolti allo studio della materia allo stato solido. In questo campo di ricerca, estremamente vasto ed
articolato, vengono messi alla prova i modelli e le predizioni della meccanica quantistica al cospetto
di insiemi grandissimi di particelle (atomi, ioni, molecole) legate fra loro per costituire i materiali
che quotidianamente osserviamo ed utilizziamo in innumerevoli occasioni. Benché tali materiali
siano pressoché illimitati nelle loro differenze di aspetto, sostanza, proprietà, caratteristiche
chimiche, fisiche, meccaniche, e così via, l’approccio tecnico della scienza fisica consente una
classificazione relativamente semplice e schematica di sostanze solide in termini di poche e bene
definite proprietà generali. C’è una prima, piuttosto ovvia distinzione fra sostanze allo stato gassoso
(nelle quali le interazioni fra i costituenti “elementari” sono trascurabili o comunque piccole), allo
stato liquido (per le quali la teoria, benché consolidata sul fronte della simulazione numerica, sia
ancora insoddisfacente da punti di vista più fondamentali), e sostanze solide. Queste ultime possono
essere differenziate in due grandi famiglie. Da un lato, vi sono i solidi cristallini, per i quali è
possibile considerare una struttura regolare, ordinata, basata su un “reticolo” di particelle (atomi,
ioni, molecole) che, oltre ad obbedire alle leggi della meccanica quantistica nelle loro interazioni,
presentano una caratteristica di sistematica previdibilità nella collocazione spaziale. Un po’ come
pensare ad una costruzione di mattoni disposti secondo una sequenza ordinata ed egualmente
ripetuta in tutto lo spazio a disposizione. Dall’altro lato, esistono sostanze amorfe, nelle quali i
“mattoni” non sono più collocati in modo ordinato ma “ammucchiati” senza regole di ordine
spaziale di alcun genere. Benché molti sistemi solidi di interesse fondamentale ed applicativo
ricadano in questa categoria (basti pensare ai vetri), la loro descrizione è molto complessa e non
verrà affrontata in questo corso. Ci interessiamo dunque solo di solidi cristallini, per i quali, come
già detto, è possibile parlare di un reticolo, ossia di un ordinamento spaziale che si può pensare
esteso indefinitamente, in corrispondenza del quale si collocano i “mattoni” che costruiscono il
solido in esame. Tali mattoni (come già detto, atomi, ioni o molecole) non vanno pensati come
entità statiche, immobili, puntiformi, bensì come unità strutturate nonché in moto più o meno
pronunciato a seconda delle situazioni, interagenti con altre unità vicine o prossime. Ciononostante,
l’idea di avere tali entità di materia disposte secondo una struttura “in media” ordinata, consente
semplificazioni e previsioni molto efficaci del comportamento fisico-chimico della sostanza
considerata. Vedremo come le proprietà “esterne” (colore, risposta meccanica) e quelle “interne”
(elettriche, magnetiche, termiche) delle sostanze a struttura ordinata siano ottenibili nel linguaggio
della meccanica quantistica in termini relativamente semplici. Un altro aspetto importante dello
studio di strutture solide cristalline è che per esse esistono tecniche di indagine sperimentale
(essenzialmente studi di diffrazione di raggi X e di neutroni) che, sfruttando interamente proprio la
regolarità del reticolo di queste sostanze, consentono di ottenere informazioni dettagliate ed
attendibili sulle proprietà della materia considerata.
2.
Solidi ionici
Nello studio delle molecole, si sono considerati legami di tipo ionico, che si instaurano in presenza
di atomi differenti i quali, a causa di uno sbilancio di carica indotto e rafforzato tra di essi, si
attirano reciprocamente. Una situazione del tutto simile esiste in quella classe di solidi cristallini i
cui componenti sono atomi con forti differenze di elettronegatività e sono disposti secondo strutture
spaziali che ottimizzano lo “impacchettamento” degli atomi stessi. Una delle strutture di base più
ricorrenti è quella cubica, con atomi (ioni) collocati ai vertici di un reticolo di cubi. A seconda del
tipo di atomi coinvolti, l’impacchettamento può condurre a due strutture distinte, quella a corpo
centrato (bcc, body-centered cubic) e quella a facce centrate (fcc, face-centered cubic). Come
Introduzione alla fisica dello stato solido - 1
raffigurato, entrambe le strutture conducono ad un’elevata densità di atomi.
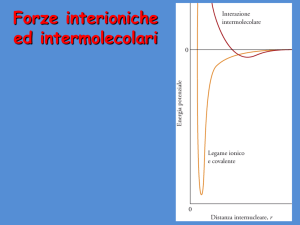
L’energia complessiva del sistema può essere calcolata a
partire da due contributi fondamentali. Si ha
l’attrazione/repulsione di natura coulombiana, elettrostatica,
ed una repulsione di natura quantistica, dovuta (come nel caso
delle molecole a carattere ionico) all’impossibilità di
avvicinare oltre una minima distanza gli ioni a causa della
repulsione fra cariche omonime (protoni ed elettroni) ma
reticolo cubico
anche a causa dell’azione del principio di Pauli sul
semplice
riempimento degli orbitali atomici da parte degli elettroni
chiamati in causa. Il reticolo fcc è leggermente più compatto del bcc, ma la
configurazione del solido dipende da vari fattori, inclusa la temperatura, oltre
reticolo fcc
naturalmente agli atomi che costituiscono il materiale. L’esempio più tipico di
solido fcc è il cloruro di sodio (sale da cucina, NaCl), che si può dunque pensare come una struttura
regolare di ioni Na+ e Cl collocati alternativamente sui vertici e sulle facce dei
cubi costituenti il reticolo. Un caso invece tipico di reticolo bcc è il cloruro di
cesio, CsCl. Questi solidi hanno un’energia di coesione che può essere calcolata
con un’operazione che tenga conto delle interazioni fra tutti gli ioni del reticolo.
Nel caso di NaCl, ad esempio, osserviamo che ogni ione di sodio ha sei primi
vicini di cloro a distanza R (il lato della “cella unitaria”), e 12 secondi vicini di
sodio a distanza R(2)1/2. Il conteggio può proseguire, per ottenere una serie di
termini a segno alterno (attrazione/repulsione coulombiana per ioni di segno
opposto/eguale) che lentamente converge ad un valore negativo per l’energia
reticolo bcc
elettrostatica del singolo ione. Per il cloruro di sodio si ottiene la seguente
espressione:
UC
e2
40
6
12
8
e2
,
40 R
R R 2 R 3
in cui la costante , detta costante di Madelung, dipende dalla struttura del reticolo e per NaCl vale
1.748, mentre per CsCl (reticolo bcc) vale 1.763. Dobbiamo ovviamente aggiungere a quest’energia
anche la repulsione quantistica/elettrostatica sopra citata. Un modello
ragionevole e semplice suggerisce di adottare un termine
del tipo A/Rn, con A ed n da determinare a seconda del
solido considerato. L’energia totale di uno ione è dunque
data dalla somma di UC e del termine repulsivo. Ci si
aspetta dunque di ottenere una dimensione reticolare di
minima energia, semplicemente calcolando la derivata
CsCl
NaCl
dell’energia ionica rispetto la coordinata reticolare R. Il
risultato è solitamente assegnato esprimendo il parametro A dell’energia repulsiva in funzione delle
altre grandezze coinvolte. L’esponente n è infatti determinabile in modo indiretto a partire da
misure di proprietà meccaniche legate alla compressibilità del cristallo. Si ottiene in definitiva che
l’energia di legame dello ione minima è data da
E B E ( Rmin )
e2 1
1 .
40 R0 n
L’energia di coesione del solido (l’energia richiesta per separarlo in tutti i suoi costituenti ionici,
ovvero l’energia richiesta per costruire l’intero cristallo) è data dall’energia di legame di ciascuno
ione moltiplicata per il numero totale di ioni. EB rappresenta infatti l’energia di legame di un singolo
Introduzione alla fisica dello stato solido - 2
ione dovuta all’interazione con tutti gli altri ioni del reticolo. Per ottenere l’energia di coesione di
una mole di ioni (NA ioni) dobbiamo prendere EB dimezzata (per non contare due volte il contributo
di legame ionico), considerare 2NA coppie di ioni e dunque l’energia di coesione è
EC=(EB/2)(2NA)=EBNA. La figura mostra l’andamento dei due contributi energetici per un singolo
ione.
Come conseguenza della struttura sopra descritta, i cristalli ionici
presentano in generale caratteristiche di elevata stabilità
meccanica e durezza (per la compattezza del reticolo), sono
conduttori elettrici estremamente poveri (non ci sono elettroni
disponibili, essendo tutti impegnati nel legame ionico), hanno
temperature di fusione/evaporizzazione molto elevate (il legame
ionico è dell’ordine di qualche eV, corrispondente a temperature
dell’ordine di qualche migliaio di gradi), sono trasparenti alla
radiazione visibile (fotoni in questo campo di frequenze hanno
energie non utili per l’eccitazione degli elettroni disponibili nel
cristallo) ma assorbono fortemente nell’infrarosso, come è
possibile verificare assumendo che la forza di richiamo fra gli ioni
Energie in un cristallo ionico
(NaCl)
sia elastica ed inserendo i valori tipici di un solido ionico. Sono
infine solidi solubili in acqua ed in altri liquidi polari, ossia con
molecole che presentano un dipolo elettrico permanente, in grado di esercitare una forza sufficiente
a rompere il legame ionico.
3.
Solidi covalenti
In totale analogia con il caso delle singole molecole covalenti, è possibile osservare solidi cristallini
i cui costituenti sono impegnati in legami con completa condivisione degli elettroni nei livelli
disponibili, ossia senza bisogno di chiamare in causa interazioni di natura elettrostatica. In questo
limite, si parla di solidi o cristalli covalenti, caratterizzati (come nel caso delle molecole
corrispondenti) da legami fortemente direzionali (basti pensare
alle ibridizzazioni sp dei composti del
carbonio). A tale proposito, una
struttura reticolare molto conosciuta è
quella del carbonio nella forma di
diamante, nella quale il reticolo ripete
una singola cella tetraedrica nello
spazio, come raffigurato. I solidi
cella tetraedrica del
covalenti presentano caratteristiche
carbonio
spesso molto differenti da quelle dei
solidi ionici, essendo ovviamente altrettanto differente la loro
reticolo del diamante
composizione. E’ peraltro più difficile definire un insieme di
proprietà comuni per i solidi covalenti, che presentano spesso
differenze notevoli di comportamento chimico fisico. Il diamante è trasparente e compatto per
l’elevata energia di legame, mentre germanio e silicio (sempre covalenti) sono opachi alla
radiazione visibili e riflettenti. Il diamante fonde a temperature molto elevate, germanio e silicio a
temperature relativamente più basse. Anche le proprietà elettriche sono estremamente differenti,
come avremo occasione di riprendere in seguito parlando di semiconduttori.
4.
Solidi molecolari
Nei solidi ionici e covalenti non è possibile parlare di molecole, in quanto la loro identità è del tutto
dissolta nella struttura reticolare del sistema. Esistono però in natura sostanze solide nelle quali le
Introduzione alla fisica dello stato solido - 3
molecole mantengono la loro identità e si uniscono con legami di natura ancora una volta
elettrostatica, benché di minore intensità. Un caso tipico è costituito dai composti solidi dell’acqua o
di altre sostanze formate da molecole polari (il ghiaccio, ad esempio). In esse le molecole si
uniscono in strutture cristalline grazie a forze elettrostatiche dipolari. Anche sostanze non polari,
ossia le cui molecole non posseggono un momento permanente di dipolo elettrico, possono formare
strutture solide cristalline. Questo è reso possibile ancora una volta da interazioni molto deboli fra
dipoli non permanenti ma indotti dai continui moti rapidissimi interni ai singoli atomi o molecole.
Un caso tipico è quello degli aggregati solidi di gas inerti (che solidificano in forma cristallina
secondo varie forme reticolari) o di aggregati solidi di molecole più complesse (dimeri e polimeri).
Il legame supportato da dipoli non permamenti è usualmente ricondotto ad un’interazione efficace
che è nota come potenziale di Van der Waals. Esistono infine solidi nei quali gli elettroni più esterni
sono così poco legati agli atomi originari da potere essere “condivisi” dai centri reticolari, portando
ad una struttura nella quale gli elettroni sono visti come un “mare” o un “gas” di particelle che, oltre
ad “incollare” fra loro gli ioni atomici (i centri del reticolo), forniscono un
efficace mezzo di conduzione sia elettrica che termica. Questi solidi, che
spesso presentano una struttura reticolare di tipo esagonale compatta
(raffigurata), sono detti solidi metallici e ad essi viene dedicato uno studio
specifico. E’ anche importante sottolineare che la classificazione qui
presentata (come tutte le classificazioni) non può essere rigidamente
assunta come unico schema di appartenenza delle innumerevoli varietà di
materiali presenti in natura o prodotti artificialmente. In molti casi si
osserveranno caratteristiche miste di comportamento. Nella forma
cristallina del carbonio detta grafite, ad esempio, convivono modalità
covalenti di legame (si forma un reticolo compatto piano a celle esagonali
di atomi di atomi) e modalità molecolari (i vari piani covalenti sono
reticolo esagonale
sovrapposti e legati da forze deboli di natura dipolare). Il risultato è che i
vari piani (che possono essere pensati come immense molecole nella forma
di griglie esagonali) possono scorrere facilmente uno sull’altro, ciò che conferisce alla grafite le ben
note proprietà lubrificanti.
5.
Teoria delle bande elettroniche
La maggior parte delle proprietà dei solidi può essere compresa, o quantomeno inquadrata con
proprietà, nell’ambito di una teoria che esplicitamente tenga conto del
modo in cui i livelli energetici a disposizione degli elettroni in un
solido si modificano in virtù del grandissimo numero di particelle
interagenti. Si consideri, ad esempio, l’interazione fra due atomi di
3s
sodio, ciascuno portatore di un elettrone spaiato nel livello 3s. Come
precedentemente studiato, gli atomi eguali, a partire da distanza molto
grande, combinano i livelli inizialmente degeneri (con eguale energia)
in due livelli con funzioni d’onda che sono combinazioni diverse
degli stati atomici separati. Il risultato è che si ottengono due energie
3s associate a configurazioni leganti e non-leganti dei due atomi. Se il
numero degli atomi di sodio aumenta, la procedura qui delineata è
essenzialmente immutata, con l’unica ed importante differenza che
ora aumenta corrispondentemente il numero di livelli energetici resi
disponibili dall’aumentato numero di singoli stati atomici interagenti.
3s Se si considera un numero elevatissimo di atomi (come capita di fatto
in un solido), l’idea qui descritta conduce alla formazione di un “quasi
continuo” di livelli energetici, una cosiddetta banda di energia, che è
semplicemente un susseguirsi fittissimo di stati energetici a disposizione per gli elettroni di tipo 3s
Introduzione alla fisica dello stato solido - 4
degli atomi coinvolti. Siccome ogni atomo contribuisce con un elettrone 3s, unendo N atomi in una
struttura solida si ottiene una banda di energia riempita da N elettroni.
Questa banda, vista la sua origine, potrebbe essere ulteriormente
3p
popolata, in quanto per ogni coppia di livelli 3s il principio di Pauli
permette le coabitazione di 2 elettroni. La banda in questione è dunque
3s
riempita solo per metà.
N
In pratica, considerando un solido composto da atomi di sodio, ci
aspettiamo una sequenza di bande energetiche associate ai livelli atomici
2p
6N
dei singoli atomi, 1s, 2s, 2p, 3s. Le bande che derivano da orbitali
atomici completi (1s, 2s, 2p) saranno complete e popolate da 2N
elettroni (le bande s) e da 6N elettroni (le bande p). La banda 3s, come
2N
2s
sopra detto, è popolata solo per metà. Esistono ovviamente altre bande
che, in assenza di eccitazione esterna (ad esempio di origine termica)
2N
1s
sono completamente vuote: ad esempio la banda 3p potrebbe accettare
6N elettroni ma nessuno la popola, in questo stato di minima energia. Questa situazione, che
corrisponde appunto allo stato fondamentale elettronico del solido di atomi di sodio, ovvero sodio
metallico, permette immediatamente di comprendere e visualizzare qualitativamente il meccanismo
di conduzione (sia elettrica che termica) ad opera di elettroni “liberi”
o di “conduzione” all’interno del metallo stesso. Si tratta di
considerare che la banda 3s è disponibile ad essere popolata da
livelli vuoti
elettroni, essendo piena solo a metà, ed anche la banda 3p, come
quelle di energia ancora più grande, sono vuote e pronte ad essere
popolate da elettroni con energia sufficiente. Questo meccanismo
livelli pieni
avviene ad opera tipicamente di schemi di eccitazione termica:
ricordando che gli elettroni, in quanto fermioni, obbediscono alla
distribuzione statistica di Fermi-Dirac, a temperatura zero sono tutti
ad energie minori dell’energia di Fermi, che dunque si colloca a metà
della banda 3s, fino a dove gli elettroni sono collocati nel metallo. Per
EF
anche piccoli aumenti di temperatura, si rendono disponibili (nel
senso statistico del termine) stati conduttivi, ossia elettroni che prima
erano “congelati” nella metà inferiore della banda 3s, possono essere
promossi ad energie più elevate (ancora nella banda 3s, oppure fino
alla banda 3p per energie crescenti) e dunque risultano liberi di
muoversi nel metallo e di condurre energia. Anche se questo
meccanismo è in realtà più complesso a causa delle collisioni con il reticolo degli ioni atomici (gli
atomi di sodio che hanno ceduto elettroni al “mare” termicamente eccitato), il motivo principale
della conduzione è quello appena descritto.
L’esempio ora visto del sodio metallico è quello di un buon conduttore, in quanto esso ha a
disposizione una banda di energia solo parzialmente occupata. Al contrario, un solido nel quale una
banda è completamente piena e la
successiva è completamente vuota,
banda di
è candidato ad essere un buon
banda di
conduzione
conduzione
isolante. Se la differenza di energia
fra queste bande consecutive (detto
gap) è maggiore di kT, il “quanto”
EF
EF
di eccitazione termica (circa 25
banda di
banda di
valenza
valenza
meV a temperatura ambiente),
assecondando la distribuzione di
Fermi-Dirac, con energia di Fermi
conduttore
isolante
semiconduttore
collocata nel gap energetico, si
comprende che questo solido non
Introduzione alla fisica dello stato solido - 5
potrà contare su elettroni liberi di sostenere meccanismi conduttivi. Il terzo caso, che verrà
comunque approfondito in altra sede, è quello in cui il gap energetico è molto piccolo. In questo
caso, per energie sufficientemente elevate, è possibile promuovere elettroni dalla banda piena (che
spesso è detta banda di valenza) a quella vuota (detta banda di conduzione). Allo stesso tempo,
liberando stati dalla banda di valenza, si ha disponibilità anche per gli elettroni di valenza di
acquistare energia e mobilità all’interno del solido. Quando un solido risponde a queste
caratteristiche è detto semiconduttore. Anticipando ulteriori approfondimenti, dovrebbe comunque
risultare già chiaro che un metallo semiconduttore risulterà relativamente sensibile ad effetti di
temperatura rispetto un metallo conduttore o isolante, vista la piccolezza del gap energetico fra le
bande di valenza e di conduzione. Inoltre è possibile modificare in modo molto ampio le proprietà
elettriche di un semiconduttore, sempre per gli stessi motivi, introducendo piccole quantità di atomi
“ospiti” nel solido, operazione detta drogaggio (doping).
Vale la pena infine sottolineare l’importanza della teoria delle bande nei solidi in quanto, almeno
apparentemente, le proprietà sopra elencate per i conduttori ed isolanti potrebbe venire bene
descritte semplicemente osservando le caratteristiche dell’atomo
singolo: che il sodio sia un buon conduttore è facilmente accettabile in
6N
quanto l’atomo ha un elettrone spaiato, come pure il fatto che lo xenon
metallico sia isolante è comprensibile in quanto nell’atomo sono
3p
impegnati tutti gli elettroni disponibili ed il legame è di tipo molecolare.
8N
Se però si prende il magnesio, atomo con il livello elettronico 3s
completo, il metallo corrispondente è invece un buon conduttore.
2N
Analogamente, per il carbonio, ci si aspetta che esso sia un buon
3s
conduttore visto che solo due dei sei elettroni 2p sono impegnati nei
legami. Il carbonio (diamante, ad esempio) è invece un eccellente
isolante. E’ dunque chiaro che la descrizione di questi (come di altri)
solidi richiede qualcosa di più
generale che non la teoria del
silicio, germanio
riempimento dei livelli atomici. La teoria delle bande
fornisce infatti l’interpretazione corretta per entrambe gli
4N
esempi. Nel caso del magnesio, si osserva che nel solido le
np
bande 3s (piena) e 3p (vuota) all’avvicinarsi degli atomi si
8N
sovrappongono per divenire un’unica banda con
ns
disponibilità totale di 8N elettroni, e riempita soltanto da
4N
2N di essi. Dunque il magnesio metallico è un buon
conduttore. Nel caso del carbonio, del germanio e del
carbonio
silicio, inizialmente le bande ns ed np (con 2N e 6N
elettroni) dopo essersi sovrapposte come nel caso del
magnesio, si separano in due bande con 4N elettroni ciascuna, entrambe complete e ben distanziate
(per il carbonio) oppure molto vicine (per silicio e germanio). Di conseguenza, il carbonio è isolante
mentre la vicinanza delle due bande spiega la natura semiconduttrice di silicio e germanio.
6.
Interazioni con i centri reticolari
La teoria delle bande di energia per gli elettroni in un solido può essere ottenuta a partire da
considerazioni relativamente semplici basate sul comportamento quantistico degli elettroni in
interazione con i centri reticolari. Si consideri, per semplicità, un “reticolo” unidimensionale, ossia
una catena di ioni immobili ed equispaziati alla distanza d. Un elettrone che viaggia con una data
energia lungo questa catena può comportarsi in due modi: è libero di propagare nel solido in quanto
la sua lunghezza d’onda è tale da escludere interazioni apprezzabili con gli ioni (detto in altro
modo, l’onda elettronica rimane essenzialmente piana e fuori fase rispetto la catena degli ioni),
oppure l’elettrone subisce collisioni con la catena di ioni. Ciò avviene in corrispondenza di
Introduzione alla fisica dello stato solido - 6
particolari coincidenze fra la lunghezza d’onda dell’elettrone e la spaziatura del reticolo, in modo
del tutto simile con i fenomeni di diffusione à la Bragg discussi precedentemente nel caso della
spettroscopia di cristalli solidi. Quando queste condizioni
si realizzano, l’elettrone si comporta come un’onda
k
stazionaria, definita dalla sovrapposizione (interferenza)
d
dell’onda incidente sullo ione e quella riflessa (diffusa).
L’onda può risultare sia rinforzata in ampiezza
(interferenza costruttiva) che diminuita (intereferenza
distruttiva). Possiamo interpretare questo risultato
ioni
ammettendo che, in corrispondenza di tali due situazioni,
l’elettrone si localizzi preferenzialmente in prossimità dei
centri reticolari (diminuendo così la sua energia, a causa dell’attrazione ione-elettrone) oppure tra di
essi (aumentando l’energia per il medesimo motivo). Se l’elettrone
non soddisfa la condizione di interferenza, la sua energia è legata
al suo numero d’onda, k=p/ћ, dalla E=p2/2m=ћ2k2/(2m), ossia
l’energia è rappresentata da una parabola in funzione del numero
d’onda. La condizione di interferenza è data da 2d=nλ, ossia
k=nπ/d. In corrispondenza di tali valori per k, l’energia
dell’elettrone sarà leggermente minore (intereferenza costruttiva) o
maggiore (intereferenza distruttiva) di quella parabolica libera. Si
osserva nell’andamento complessivo che il momento dell’elettrone
definisce automaticamente una serie di “zone” (dette di Brillouin)
π/d 2π/d
entro le quali l’elettrone è “intrappolato”. Allo stesso tempo, le 2π/d π/d
k
zone di Brillouin (associate appunto alle varie condizioni di
interferenza per valori crescenti di n) definiscono una sequenza a bande dell’energia dell’elettrone.
Questo risultato, ora ottenuto senza calcoli espliciti, oltre a trovare diretta conferma in svariate
situazioni sperimentali, è raffinabile a vari livelli introducendo forme esplicite, più o meno
complesse di potenziali periodici che rappresentano i centri reticolari e le loro interazioni con gli
elettroni. Vedremo, nel capitolo dedicato ai fenomeni conduttivi, semiconduttivi e superconduttivi
come la teoria delle bande combinata con la statistica di Fermi-Dirac dia risposte precise sulla
natura e sulle caratteristiche dettagliate di pressoché l’intera famiglia dei solidi cristallini.
7.
Esercizi
(a) Sapendo che l’energia di coesione del cristallo NaCl è pari a 769103 J/mol,
determinare l’energia di legame di una coppia di ioni nel solido.
(b) Sapendo che il passo reticolare di NaCl è pari a 0.281 nm ed n=9 (l’esponente nel
potenziale ionico repulsivo), confrontare il risultato dell’esercizio precedente con il
valore ottenuto dall’espressione per l’energia di legame ionico riportata nel testo.
(c) Calcolare l’energia richiesta per atomo neutro richiesta per separare nelle sue
componenti un cristallo NaCl.
(d) Utilizzando le espressioni date nel testo, ed assumendo che la forza fra ioni sia di
natura elastica (imponendo piccoli spostamenti dalla coordinata di equilibrio),
verificare che un cristallo di NaCl è un buon assorbitore nell’infrarosso.
Introduzione alla fisica dello stato solido - 7