PSfrag replacements
Modulo o "valore assoluto"
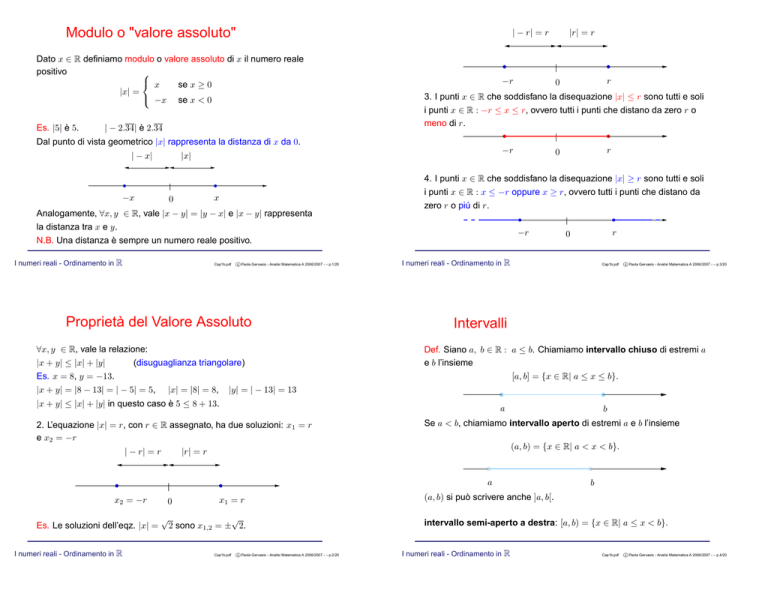
Dato x ∈ R definiamo modulo o valore assoluto di x il numero reale
positivo
x
se x ≥ 0
|x| =
−x se x < 0
Es. |5| è 5.
| − 2.34| è 2.34
PSfrag replacements
Dal punto di vista geometrico |x| rappresenta la distanza di x da 0.
| − x|
|x|
−x
PSfrag replacements
Analogamente, ∀x, y ∈ R, vale |x − y| = |y − x| e |x − y| rappresenta
−r
0
−r
0
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.1/20
Proprietà del Valore Assoluto
∀x, y ∈ R, vale la relazione:
|x + y| ≤ |x| + |y|
(disuguaglianza triangolare)
Es. x = 8, y = −13.
|x + y| = |8 − 13| = | − 5| = 5,
−r
|x| = |8| = 8,
Cap1b.pdf
[a, b] = {x ∈ R| a ≤ x ≤ b}.
a
|r| = r
Es. Le soluzioni dell’eqz. |x| =
I numeri reali - Ordinamento in R
0
b
Se a < b, chiamiamo intervallo aperto di estremi a e b l’insieme
(a, b) = {x ∈ R| a < x < b}.
PSfrag replacements
√
x1 = r
√
2 sono x1,2 = ± 2.
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.2/20
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.3/20
Def. Siano a, b ∈ R : a ≤ b. Chiamiamo intervallo chiuso di estremi a
e b l’insieme
a
x2 = −r
r
0
Intervalli
|y| = | − 13| = 13
2. L’equazione |x| = r, con r ∈ R assegnato, ha due soluzioni: x1 = r
Sfrag replacements
e x2 = −r
| − r| = r
r
I numeri reali - Ordinamento in R
PSfrag replacements
|x + y| ≤ |x| + |y| in questo caso è 5 ≤ 8 + 13.
r
4.
punti
| −I r|
= rx ∈ R che soddisfano la disequazione |x| ≥ r sono tutti e soli
i punti
x r∈ R : x ≤ −r oppure x ≥ r, ovvero tutti i punti che distano da
|r| =
zero r o piú di r.
la distanza tra x e y.
N.B. Una distanza è sempre un numero reale positivo.
I numeri reali - Ordinamento in R
|r| = r
3.
punti
| −I r|
= rx ∈ R che soddisfano la disequazione |x| ≤ r sono tutti e soli
i punti
x r∈ R : −r ≤ x ≤ r, ovvero tutti i punti che distano da zero r o
|r| =
meno di r.
PSfrag replacements
x
0
| − r| = r
b
(a, b) si può scrivere anche ]a, b[.
intervallo semi-aperto a destra: [a, b) = {x ∈ R| a ≤ x < b}.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.4/20
PSfrag replacements
a
intervallo semi-aperto a sinistra: (a, b] = {x ∈ R| a < x ≤ b}.
a ≤ x,
(a, +∞) = {x ∈ R| a < x}
oppure (−∞, b] = {x ∈ R| x ≤ b},
(−∞, b) = {x ∈ R| x < b},
Es. A = (−∞, 1). A è superiormente limitato, ma non inferiormente
In generale: un intervallo si dice chiuso se include i suoi estremi,
aperto se esclude i suoi estremi.
Def. I punti dell’intervallo che non sono estremi dell’intervallo sono
detti punti interni.
eplacements
Es. A = [−1, 1) ∪ {2}. Qualunque a ≤ −1 è minorante di A. A è
superiormente e inferiormente limitato.
Si definisce la Retta estesa R = R ∪ {−∞, +∞} = [−∞, +∞]
Cap1b.pdf
∀x ∈ A.
Ogni a che soddisfa tale relazione è detto un minorante di A.
dove i simboli −∞ e +∞ non indicano numeri reali, permettono di
estendere l’ordinamento dei reali, attraverso la convenzione che
∀x ∈ R, −∞ < x < +∞.
I numeri reali - Ordinamento in R
R
Def. Sia A ⊂ R. Diciamo che A è inferiormente limitato se esiste un
numero reale a tale che:
Intervalli definiti da una sola disuguaglianza:
[a, +∞) = {x ∈ R| a ≤ x},
A
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.5/20
limitato: tutti i numeri reali x ≥ 1 sono maggioranti di A, mentre non
esistono minoranti di A.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.7/20
Insiemi limitati
A
b
R
Def. Sia A ⊂ R. Diciamo che A è superiormente limitato se esiste un
numero reale b tale che:
eplacements
x ≤ b,
∀x ∈ A.
−2
Ogni b che soddisfa tale relazione è detto un maggiorante di A.
Es. A = {x ∈ R| − 1 ≤ x < 1}. b = 1, b = 10, b = 1000 sono
A
1
5
non esiste b ∈ R maggiorante di N.
Proprietà di Archimede
Def. Si dice che A è limitato se è contemporaneamente
superiormente e inferiormente limitato.
maggioranti di A. Qualunque b ≥ 1 è maggiorante di A.
−1
Es. N ⊂ R è inferiormente limitato, ma non superiormente. Qualunque
a ≤ 0 è un minorante di N, ma:
R
L’intervallo [−5, π) è limitato. I suoi minoranti sono tutti i numeri reali
x ≤ −5, i suoi maggioranti sono tutti i numeri reali x ≥ π
Es. A = [−1, 1) ∪ {2}. Tutti i b ≥ 2 sono maggioranti di A, b = 1.6 non è
maggiorante di A.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.6/20
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.8/20
Massimo e minimo di un insieme
Def. Diciamo che un insieme A ⊂ R ammette massimo se esiste un
elemento xM ∈ A tale che
x ≤ xM
∀x ∈ A.
L’elemento xM viene chiamato massimo dell’insieme A e si indica
con xM = max A.
Oss. Un insieme che ammette massimo è anche superiormente
limitato e xM = max A è un maggiorante di A.
Proprietà: Se un insieme A ha massimo, allora max A è il piú piccolo
dei maggioranti di A.
Es. A = (−5, 2]. max A = 2 e ogni x ≥ 2 è maggiorante di A.
Es. A = {x ∈ Q| x2 − 2 < 0}. A è limitato in R, ma non ha massimo e
minimo.
√
√
Infatti si può anche scrivere A = {x ∈ Q| − 2 < x < 2}.
√
I maggioranti di A sono tutti i numeri reali x ≥ 2. I minoranti di A
√
√
√
sono tutti i numeri reali x ≤ − 2, ma ± 2 6∈ Q e quindi ± 2 6∈ A.
√ √
√
√
N.B. La scrittura (− 2, 2) è equivalente a {x ∈ R| − 2 < x < 2} e
√
√
non a {x ∈ Q| − 2 < x < 2}.
√
√
Es. A = {x ∈ R| x2 − 2 ≤ 0} = {x ∈ R| 2 ≤ x ≤ 2}.
A è limitato in R ed ha massimo e minimo.
√
Infatti, stavolta ± 2 ∈ A.
Oss. Un insieme che è superiormente limitato non è detto che abbia
massimo:
Es. A = (−5, 2). @xM ∈ A maggiore o uguale di tutti gli elementi di A.
N.B. x = 2 6∈ A.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.9/20
Def. Diciamo che un insieme A ⊂ R ammette minimo se esiste un
elemento xm ∈ A tale che
xm ≤ x
∀x ∈ A.
L’elemento xm viene chiamato minimo dell’insieme A e si indica con
xm = min A.
Oss. Un insieme che ammette minimo è anche inferiormente limitato e
xm = min A è un minorante di A.
Proprietà: Se un insiema A ammette minimo, allora min A è il piú
grande dei minoranti di A.
Es. A = [−5, 2). min A = −5 e ogni x ≤ −5 è minorante di A.
Oss. Un insieme che è inferiormente limitato non è detto che abbia
minimo:
Es. A = (−5, 2). @xm ∈ A minore o uguale di tutti gli elementi di A.
N.B. x = −5 6∈ A.
Teorema. Massimo e minimo, se esistono, sono unici.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.10/20
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.11/20
Estremi inferiore e superiore
Def. Sia A ⊂ R superiormente limitato. Chiamiamo estremo
superiore di A il più piccolo dei maggioranti di A e lo denotiamo con
sup A.
Sia A ⊂ R inferiormente limitato. Chiamiamo estremo inferiore di A il
più grande dei minoranti di A e lo denotiamo con inf A.
Oss. Se un insieme ha massimo, allora tale numero è anche estremo
superiore. Il viceversa non è vero.
Se un insieme ha minimo, allora tale numero è anche estremo
inferiore. Il viceversa non è vero.
√ √
√
√
Es. A = (− 2, 2], max A = 2 = sup A, inf A = − 2.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.12/20
Caratterizzazione matematica del sup
Il sup A è caratterizzato dalle seguenti due condizioni:
1) ∀x ∈ A, x ≤ sup A
(ovvero sup A è un maggiorante di A)
Proprietà. Se esistono inf e sup di un insieme, questi sono unici.
Se un insieme non è superiormente limitato, diciamo che
sup A = +∞
2) ∀r ∈ R, r < sup A, ∃x ∈ A| x > r.
(ovvero sup A è il piú piccolo dei maggioranti di A, perché un qualsiasi
altro numero reale r minore di sup A non è piú maggiorante di A)
Sfrag replacements
x
r
I numeri reali - Ordinamento in R
Se un insieme non è inferiormente limitato, diciamo che
inf A = −∞
sup A
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.13/20
I numeri reali - Ordinamento in R
2) ∀r ∈ R, r > inf A, ∃x ∈ A| x < r.
(ovvero inf A è il piú grande dei minoranti di A, perché un qualsiasi
altro numero reale r maggiore di inf A non è piú minorante di A)
Sfrag replacements
x
sup A
infA
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.15/20
Stavamo analizzando le proprietà di R
Caratterizzazione matematica dell’inf
L’inf A è caratterizzato dalle seguenti due condizioni:
1) ∀x ∈ A, x ≥ inf A
(ovvero inf A è un minorante di A)
Cap1b.pdf
1. Le operazioni di Q si estendono a R
2. Su R c’e’ un ordinamento totale: ≤
intervalli aperti e chiusi, insiemi superiormente ed inferiormente
limitati, maggioranti e minoranti, massimo e minimo, sup e inf.
3. I numeri razionali sono densi tra i numeri reali, ovvero tra due
numeri reali qualsiasi, esistono infiniti numeri razionali.
4. L’insieme dei numeri reali è completo: geometricamente vuol dire
che ogni punto della retta è associato ad un unico numero reale.
r
Questa proprietà permette di risolvere equazioni come x2 − 2 = 0 che
non hanno soluzione in Q.
I numeri reali - Ordinamento in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.14/20
I numeri reali
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.16/20
PSfrag replacements
3. Q è denso in R
C2
ovvero: Tra due numeri reali qualsiasi esistono infiniti numeri razionali
Es. Consideriamo i numeri reali
π = 3.1415926535897932384626433832785....
x = 3.1415926535897932384726433832785....
I numeri
3.141592653589793238463
3.141592653589793238464
..
.
3.141592653589793238471
sono tutti razionali (hanno rappresentazione decimale finita), ma anche
3.1415926535897932384631, 3.1415926535897932384632, ...
3.1415926535897932384639, ..., 3.1415926535897932384709
sono tutti razionali, ecc.
I numeri reali - Q è denso in R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.17/20
4. La completezza di R
disgiunti di R (C1 ∩ C2 = ∅) tali che C1 ∪ C2 = R e tali che ogni
elemento
di C1 sia minore o uguale di ogni elemento di C2 .
PSfrag replacements
R
C1
R
C1
s
Def.
detto elemento
I numeri
realis- viene
La completezza
di R
R
=
Q
∪
(R \ Q)
reali
=
razionali
∪
irrazionali
Sia Q che (R \ Q) sono densi in R.
L’Assioma di completezza di R implica che: "Ogni sottoinsieme di R
superiormente (risp. inferiormente) limitato ammette in R estremo
Fine di R.
superiore (risp. inferiore)".
I numeri reali - La completezza di R
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.19/20
Esercizio: Individuare le proprietà dei seguenti intervalli (aperto,
chiuso, semi-aperto a destra o a sinistra, limitato); individuare inf e sup
e, qualora esistano, anche min e max.
(−5, 4],
(−∞, 0),
{x ∈ R : |x| < 3},
{x ∈ R : |x| ≤ π},
[−2π, 2π),
{x ∈ R : x2 ≤ 2}.
Esercizio: individuare inf, sup, maggioranti e minoranti dei seguenti
insiemi e, qualora esistano, anche min e max.
C2
x1 ≤ s ≤ x 2
Geometricamente, la completezza significa che ovunque io tagli in due
la retta reale R, il punto di confine s tra le due semirette rappresenta
un (!) numero reale.
La retta R è un continuo di punti. Al contrario Q non è rappresentabile
con una retta, perchè è un sottoinsieme discreto della retta.
]2, 18[,
C2
Allora ∃!s ∈ R :
s
Riferimento bibliografico: C. Canuto, A. Tabacco: Analisi Matematica 1,
seconda edizione. Capitolo 1, pag. 14-19; Esercizi: pag 26-31.
L’insieme dei numeri reali R è completo ovvero verifica la seguente
proprietà detta Assioma di completezza o Assioma di Dedekind.
Siano C1 , C2 ⊂ R due classi contigue, ovvero due sottoinsiemi
Sfrag replacements
R
C1
∀x1 ∈ C1 , ∀x2 ∈ C2 .
separatore delle
classi.
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.18/20
Cap1b.pdf {x ∈ R : |x| > 4},
{x ∈ R : |x| < 3 ∨ |x| > 8},
{x ∈ R : |x| ≤ π ∧ |x| > 2},
(2, 10],
{x ∈ R : x ≤ 2} ∩ {x ∈ R : x > 1},
(
)
r
2
3 x − 3
x∈R:
≥0 .
3x + 5
2
I numeri reali
3
[−2π, 2π) ∪ {6},
Cap1b.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.20/20