Elementi di calcolo vettoriale
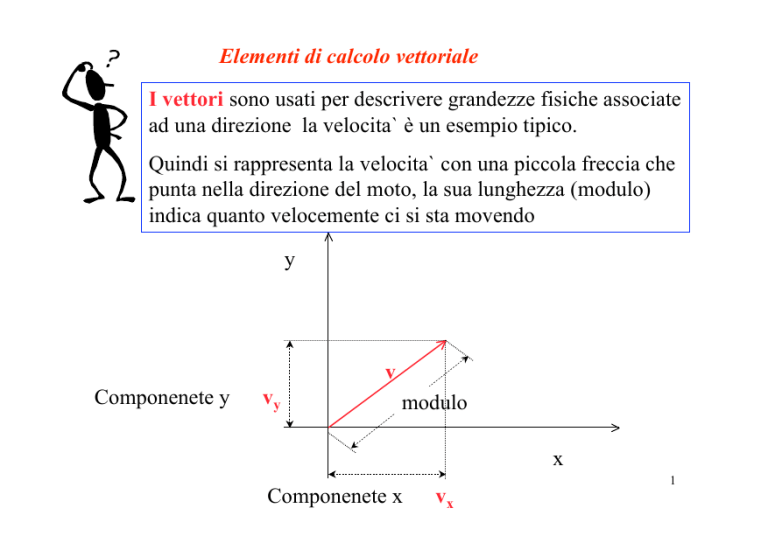
I vettori sono usati per descrivere grandezze fisiche associate
ad una direzione la velocita` è un esempio tipico.
Quindi si rappresenta la velocita` con una piccola freccia che
punta nella direzione del moto, la sua lunghezza (modulo)
indica quanto velocemente ci si sta movendo
y
v
Componenete y
vy
modulo
x
Componenete x
vx
1
COMPONENTE DI UN VETTORE
(lungo una direzione)
vy = v sen α
vx = v cos α
v y 2 + vx 2 =
= v2 sen2α + v2 cos2α =
= v2(sen2α + cos2α) =
= v2
direzione
y
vy
o
vx
v→
α
x
2
VERSORE
modulo = 1
→
direzione v
→
verso v
→
n = v
v
→
→
n ≡ direzione e verso
→
esempio di componente di un vettore
n
→
Fn = F cos !
Fn
F
!
ΔS
3
SOMMA DI VETTORI
regola del parallelogramma
(metodo grafico)
v1
→
v3
→
→
→
v1 + v2 =
→
v3
→
v2
4
SOMMA DI VETTORI
metodo per componenti
(metodo quantitativo)
y
v1y
v3x = v1x + v2x
v3y = v1y + v2y
→
v1
v3y
o
v2y
v3
→
v1x
α
v2x
v3x
x
→
v2
3 dimensioni : componente z
v3 =
2
2
v3x + v3y
v3y
tg α = v
3x
5
Somma e differenza di vettori
a1
10m
b1
15m
+
a2
10m
15m
+
a3
b2
b3
+
b
15m
=
c1
5m
c2
a3
b3
c3
18m
Somma di due vettori a+b: Regola del
parallelogramma
a+b
a
a-b
b
25m
=
=
10m
Differenza di due vettori
a
r r r
rLa somma c = a + b è tale che
c = (ax + bx ) xˆ + (ay + by )yˆ
6
PRODOTTO SCALARE
→
v1
v1 • v2 = v1 v2 cos φ
→
→
v2
φ
→
→
→
→
→
v1 • v2 = v1x v2x + v1y v2y*
→
→
v 1 • v2 = v 2 • v1
→
→
→
→
→
→
→
v1 • (v2 + v3) = v1 • v2 + v1 • v3
3 dimensioni : componente z
* + v1z v2z
7
PRODOTTO SCALARE
→
v1
v1 • v2 = v1 v2 cos φ
→
→
→
v2
φ
→
φ=0
v1
→
v2
→
→
→
→
→
→
v1 • v2 = v1v2 cos φ = v1v2
→
φ = 90°
v1
→
→
φ = 180°
v1
v2
→
v2
v1 • v2 = v1v2 cos φ = 0
v1 • v2 = v1v2 cos φ = – v1v2
8
a
c=-2a
Moltiplicazione di un vettore per un numero
y
Scomposizione di un vettore nelle sue componenti
sugli assi in un sistema cartesiano
a
ay
x
ax
b
r
)
a = ax xˆ + ay y
Il Prodotto scalare di due vettori è uno
scalare ossia un numero
θ
a
a • b = abcosθ
9
Alcuni esempi
Dati due vettori a=3.0i+3.0j+3.0k e b=2.0i+1.0j+3.0k si determini l’angolo compreso
axbx+ayby+azbz=abcosθ a=(ax2+ay2+az2)1/2 b=(bx2+by2+bz2)1/2
6+3+9=5.2∗3.7cosθ da cui cosθ =0.9 ossia θ=(25.8)o…..
Un motore trascina una massa m=150kg su un piano inclinato liscio che forma un
angolo θ=30o con l’orizzontale. La massa sale con velocita`costante. Calcolare la forza
esercitata dal motore
Ftot=0 Fmotore=mgsinθ=735N
mg
Un corpo scivola lungo un piano inclinato di 15o con velocita` costante. Calcolare il
coefficiente d’attrito fra il corpo e il piano.
Fr=µN=µ(mgcosθ) poiché la velocita` è costante Fr=mgsinθ e
quindi µ =sin15/cos15=0.27
10
Un uomo deve attraversare un fiume largo l=0.8km.Punta la barca verso la riva
opposta e rema con una velocita` v=3.2km/h rispetto all’acqua. La corrente ha una
velocita` di 6.4km/h.
Quanto tempo impiega l’uomo ad attraversare il fiume?
In quale punto della riva opposta approdera` ?
vx=6.4km/h
(0,0)
(1.6,0.8)
vy=3.2km/h
y-yo=v yt da cui
t=0.8/3.2=1/4 h
vx=6.4km/h
x-xo=vxt=1.6km
vy=3.2km/h
y-yo=vyt=0.8km
11
Esempio: la seguente tabella dà la posizione di un corpo in funzione del tempo
•Qual’è la velocità media del corpo nei primi 5 secondi del moto? Nei primi 8
secondi del moto? Nell’intero tragitto?
• Qual’è la velocità media nell’intervallo t1 =3s e t 2=7s e nell’intervallo t1 =4s e t 2=6s
•Riportare i valori della tabella in un grafico ed interpolare i punti con una curva
continua, quindi stimare la posizione del corpo negli istanti t=4.5s e t=5.5s , stimare
la velocità media in questo intervallo
•Disegnare la tangente al diagramma per t=5s e determinare in quell’istante la
velocità istantanea e confrontarla con la vm calcolata nei punti precedenti
•Calcolare la velocità istantanea agli istanti t=1s e t=9s
t(sec)
0
1
2
3
4
5
6
7
8
9
10
x(m)
0
2.3
8.4
17.1
27.2
37.5
46.8
53.9
57.6
56.7
50
•Valutare sul grafico la posizione del corpo nell’istante in cui si ferma e il momento
in cui ciò avviene
x(m)
70
60
50
40
x(m)
30
20
10
0
0
2
4
6
8
10
12
t
12
Ay=Asenθ
A
Dati due vettori A e B, determinare il vettore C
somma dei due
θ
Ax=Acosθ
C
B
A
A=15 con un angolo θ=30o rispetto all’orizzontale
B=30 con un angolo θ=60o rispetto all’orizzontale
13