Linea di Trasmissione (riassunto)

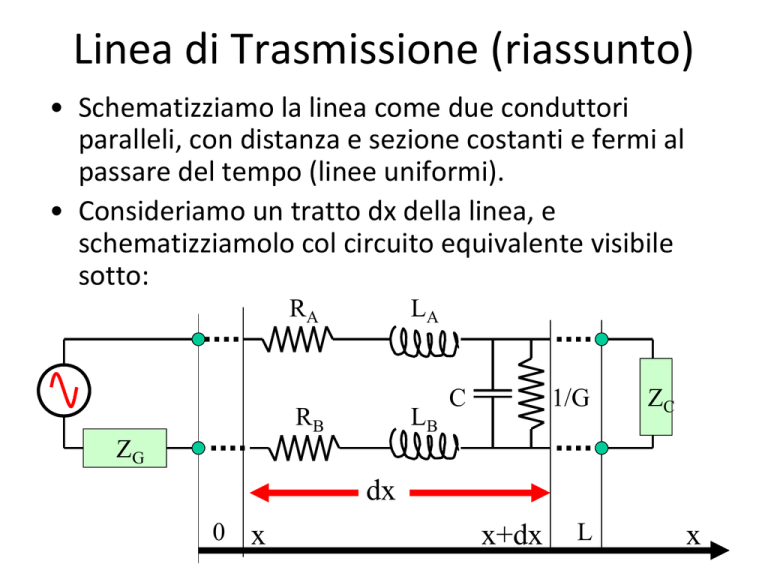
Linea di Trasmissione (riassunto)
• Schematizziamo la linea come due conduttori paralleli, con distanza e sezione costanti e fermi al passare del tempo (linee uniformi).
• Consideriamo un tratto dx della linea, e schematizziamolo col circuito equivalente visibile sotto:
RA
LA
RB
ZG
LB
C
1/G
ZC
dx
0 x
x+dx
L
x
 V ( x )
  x   Z u I ( x )
 I ( x)

  Y u V ( x )
 x
(riassunto)
dove


Zu   Ru  Lu 
t 



Yu  Gu  C u 
t 

  2V ( x )

I ( x )  Z u YuV ( x )
  Z u 

2
x
x
 2
  I ( x )   Y u   V ( x )  Z u Y u I ( x )
  x 2
x
Equazioni dei
Telegrafisti
Zu
V(t)
Yu
ZC
ZG
0 x
dx
x+dx
L
x
Soluzione per la tensione (riassunto)
• La soluzione in regime sinusoidale è
V ( x , t )  A1 e
 A2 e
 x
x
Onda progressiva
cos  t   x   1 
cos  t   x   2 
Onda regressiva
• Le due onde si propagano nella linea con velocità di fase (=Im()=Im(sqrt(ZuYu)))

Per l’onda progressiva
v


v 
Per l’onda regressiva

Soluzione per la corrente
(sinusoidale)
• Dall’ eq. dei telegrafisti
1 V ( x )
V ( x )

  Z u I ( x )  I ( x )  
x
Z u x
  x
   x   x
1    x
 


A1 e  A 2 e
A1 e  A 2 e
Z u x
Zu





  x
Z u Yu   x

A1 e  A 2 e
Zu
Zu
e' una impedenza
Yu

1
Zu
Yu


  x
  x
A1 e  A 2 e

Z o  Z o e j 

R u  j Lu
G u  j C u


Soluzione
per la corrente

I ( x , t )  Re I ( x ) e j  t 
  x
  x 
 1
(sinusoidale)
A
e
A
e
 Re 


1
2
j
Z
e
 o

A1   x
I ( x, t) 
e
cos  t   x   1    
Onda progressiva
Zo


Onda regressiva
A2  x
e

cos  t   x   2   
Zo
• Da confrontare con:
V ( x , t )  A1 e   x cos  t   x   1 
 A 2 e   x cos  t   x   2 
• Si vede che per ciascuna onda il rapporto tra tensione e corrente vale Zo. Inoltre c’è uno sfasamento -.
Usando la notazione solita:

Z o  Z o e j 
Ru  jLu

Gu  jCu
Ru  jLu

(Gu  jCu ) /(Gu  jCu )
Gu  jCu
( Ru  jLu )(Gu  jCu )


2
2 2
Gu   Cu
( Ru Gu   2 Lu Cu )  j ( Lu Gu  Ru Cu )

Gu2   2Cu2
Soluzione per la corrente
(sinusoidale)

1/2
 Im( Z o ) 
  G u L u  R u C u  
   arctg 
  arctg 

2
 Ru G u   Lu C u 
 Re( Z o ) 
• Lo sfasamento è nullo – Per linea non distorcente G u L u  R u C u
– Per linea non dissipativa R u  0 G u  0
– Per alte frequenze
R u   L u
G u   C u
R u  j Lu

• In tutti questi casi G u  j  C u

Lu
Z o 
 Ro
C u

Z o  Z oe
j

Zo 

Lu
 Ro
Cu
• Cioè l’ impedenza si riduce a una resistenza.
Lu
 Ro
Cu
Segnali Impulsivi
• Per segnali non sinusoidali la trattazione si complica molto. Ma abbiamo visto che almeno nel caso non dissipativo le diverse componenti sinusoidali si propagano tutte allo stesso modo.
• Studiamo quindi questo caso in generale:
V (x, t) 

 x  Ru  Lu t I (x, t)




I
x
t

(
,
)




 Gu  Cu V (x, t)
 x
t 

I (x, t)
 V (x, t)
 x  Lu t
I (x, t)
V (x, t)

 Cu
t
 x
• Derivando la prima rispetto a x e la seconda rispetto a t:
2
 2V ( x, t)
 I ( x, t)
2
2
 x2  Lu xt
 V ( x, t)
 V ( x, t)

 Cu Lu
0
 2
2
2
2
(
,
)
(
,
)


V
x
t
I
x
t
x
t

 Cu
 xt
t 2
Equazione delle onde
Segnali Impulsivi
 V ( x, t)
 V ( x, t)
0
 Cu Lu
2
2
x
t
2
2
• La soluzione generale è del tipo V ( x, t )  f1 ( x  vt )  f 2 ( x  vt ) con v 
• Analogamente si trova l’ equazione per I, che ha soluzione
1
Lu Cu
I ( x, t )  g1 ( x  vt )  g 2 ( x  vt )
V (x, t)
I (x, t)
 Lu
• Sostituendo nella si ottiene
x
t
1

 V (x, t)  f1(x  vt)  f2 (x  vt)
v


LuCu
I (x, t)  1  f (x  vt)  f (x  vt) dove 
1
2

R  L / C
Ro
u
u
 o


[ f1 ( x  vt )  f 2 ( x  vt )]   Lu [ g 1 ( x  vt )  g 2 ( x  vt )]
x
t
ma


 ( x  vt )


x
 x  ( x  vt )
 f1
 ( x  vt )
f 2
 ( x  vt )


 ( x  vt )
x
 ( x  vt )
x
g1
 ( x  vt )
g 2
 ( x  vt )
  Lu [


 ( x  vt )
t
 ( x  vt )
t
 f1
f 2
g1
g 2
(  v )  Lu
(v ) 

  Lu
 ( x  vt )  ( x  vt )
 ( x  vt )
 ( x  vt )
  f1
f1
 g1
L
v
g




1
u
(
)
(
)
x
vt
x
vt
Lu v





 f 2
g 2
f2
  Lu v
 g2  

 ( x  vt )
Lu v
  ( x  vt )
f1 ( x  vt ) f 2 ( x  vt )

I
Lu v
Lu v
ma
v
R0 
1

Lu C u
v
1
Lu / C u 

 Lu v  R0
R0 Lu
1

 V (x, t)  f1(x  vt)  f2 (x  vt)
v


LuCu
I (x, t)  1  f (x  vt)  f (x  vt) dove 
1
2

R  L / C
Ro
u
u
 o
Segnali Impulsivi
1

 V (x, t)  f1(x  vt)  f2 (x  vt)
v


LuCu
I (x, t)  1  f (x  vt)  f (x  vt) dove 
1
2

R  L / C
Ro
u
u
 o
• Ci aspettiamo quindi le solite onde progressive e regressive
• Ad alte frequenze ci aspettiamo anche che siano attenuate durante la loro propagazione di exp(-x).
• Inoltre ci aspettiamo che l’ impedenza della linea (rapporto tra V e I per ciascuna delle onde) sia Ro.
2

 Cu  ln(D / d )
1
1
c
 v




  R
Cu Lu
Lu  ln(D / d )

2
Segnali Impulsivi
2

 Cu  ln(D / d )



Lu  ln(D / d )

2
c
1
1

v




Cu Lu

R

R  L / C  1  /  ln(D / d )
u
u
 o
2
• Numeri tipici per l’ RG-58:
R=2, v=c/sqrt(2)
• Cu=100 pF/m
• Ro=50
• v=20cm/ns
=5ns/m
• Quindi un cavo di 100m introduce un ritardo di 500 ns.
Segnali Impulsivi
• Supponiamo di collegare la linea
ad un generatore con R interna pari Vg
a Rg, e che genera un impulso
ampio Vg per un tempo T.
• Il generatore “vede” un carico di
0
impedenza Ro, almeno finche’ non
arriva l’ onda regressiva dall’ altra
estremita’.
Vg
• Quindi nel punto x=0 a t=0 e per
un tempo2tl=2l/v si ha
1
0
1
Ro

V ( x  0, t )  Vin  Vg R  R

o
g

1
 I ( x  0, t )  I in  Vg
Ro  Rg

Senza linea
2
3
4
t(s)
Con linea
(adattata)
2
3
4
t(s)
Linea Adattata
• Al tempo t= tl=l/v il segnale arriva all’ estremità opposta della linea, attenuato di exp(-l):
V ( x  l , t )  V out  V in e   l

V out

I (x  l,t) 

Ro
• La seconda eq. deriva dal fatto che c’è solo l’ onda progressiva.
• Quello che avviene successivamente dipende da come è terminata la linea. Supponiamo che sia chiusa su una resistenza Rc. Nell’ attimo in cui il segnale arriva all’ estremità trova la resistenza Rc che chiude la linea.
• Se Rc= Ro non c’è cambiamento, perchè V(x,t)/I(x,t)= Ro come era nella linea. La resistenza Ro assorbe completamente ed esattamente le tensioni e correnti arrivate in quel punto, e quindi non parte l’ onda regressiva – non c’è riflessione. Si dice che la linea è adattata.
Linea Aperta
• Se la linea è aperta (Rc=infinito) in x= l ci deve essere sempre I(x= l )=0. Possiamo garantire che questo avvenga sovrapponendo all’ onda progressiva che è arrivata fin lì una onda regressiva (riflessa) tale che le correnti generate dalle due onde si annullino perfettamente. Avremo quindi
0  I ( x  l , t )  I out  I rifl

I rifl   I out
e anche Vrifl  Vout
definendo il coefficiente di riflessione  
Vrifl
Vout
si ha in questo caso   1. Quindi sommando le due onde :
V ( x  l , t  tl )  Vrifl  Vout  2Vin e l
Linea Aperta
• Quest’ onda riflessa comincia a viaggiare indietro lungo la linea, e al tempo t= 2tl=2l/v arriva all’ ingresso della linea, attenuata di un ulteriore fattore exp(-l).
2l
• A t= 2tl la tensione in ingresso sale quindi a Vin  Vin e
Linea aperta
Vg
0
1
2
3
4
t= 2tl=2l/v
t(s)
Linea Aperta
• Quindi all’ ingresso vedremo un’ onda di questo genere: Senza linea
Vg
0
1
2
3
4
Linea aperta
Vg
t=2tl=2l/v
Finisce l’
Impulso originale
Vin  Vin e 2l
Ro
Vin  Vg
Ro  Rg
Arriva l’ “eco” dell’ impulso
Finisce l’
“eco” dell’ impulso t(s)
Vin e 2l
0
1
2
3
4
t(s)
Linea Aperta
• Consideriamo adesso un punto diverso, a distanza x da quello iniziale: in ogni punto della linea avremo la sovrapposizione di onda progressiva e onda regressiva: per tl <t< 2tl
V ( x , t )  Vin e
- 
 Vout e
 (   x )
 [( t  t  )  (   x ) / v ] 
 Vin e -   Vin e   e  (   x ) [( t  t  )  (   x ) / v ] 

 Vin e
• Dove
- 
e
 [( t  t  )  (   x ) / v ]
 ( 2   x )
(z)
1
0
0
z
Linea in corto
• Se la linea è in corto (Rc=0) in x= l ci deve essere sempre V(x= l )=0. Possiamo garantire che questo avvenga sovrapponendo all’ onda progressiva che è arrivata fin lì una onda regressiva (riflessa) tale che le tensioni generate dalle due onde si annullino perfettamente. Avremo quindi
0  V ( x  l, t )  Vout  Vrifl
e quindi  
Vrifl
Vout

Vrifl  Vout
 1
Quindi sommando le due onde :
V ( x  l, t  tl )  Vrifl  Vout  0
1
Vout
I ( x  l, t  tl )  (Vout  Vrifl )  2
Ro
Ro
Linea in corto
• Quest’ onda riflessa comincia a viaggiare indietro lungo la linea, e al tempo t= 2tl=2l/v arriva all’ ingresso della linea: Se non fosse attenuata annullerebbe perfettamente la tensione del generatore. Ma è attenuata un fattore exp(-2l): V  V e 2l
in
Vg
Linea in corto
0
1
2
3
4
t= 2tl=2l/v
t(s)
in
Linea in corto
Senza linea
• Quindi all’ ingresso vedremo un’ onda di questo genere: Vg
0
1
2
3
4
Linea in corto
Vg
Ro
Ro  Rg
Vin  Vin e 2l
t(s)
Vin  Vg
t=2tl=2l/v
Finisce l’
Impulso originale
Arriva l’ “eco” dell’ impulso
 Vin e
Finisce l’
“eco” dell’ impulso 2l
0
1
2
3
4
t(s)
In generale
• Per Rc qualsiasi ricaviamo il coefficiente di riflessione imponendo la legge di Ohm per Rc :
V ( x  , t  t  )
 Rc
I ( x  , t  t  )
Vin e   Vin e 
 Rc


Vin e
Vin e

Ro
Ro
1   Rc


1   Ro
• Si verifica facilmente che  vale 0 per Rc=Ro, vale 1 per Rc infinita e vale –1 per Rc =0.
• In ingresso  2 

V ( x  0, t  2t  )  Vin 1   e

• Tutto questo verrà verificato sperimentalmente nell’ultima esperienza del corso (10/6/2015).
1   Rc

1   Ro

V ( x  0 , t  2 t  )  Vin 1   e 2 

Esperienza del 20/5/2015
Circuito RLC con segnali impulsivi
• Lo scopo dell’esperienza è verificare il L
comportamento sottosmorzato, criticamente smorzato, e sovrasmorzato R
dei circuiti RLC serie quando il segnale in V (t )
ingresso è un impulso ad onda quadra. • Un breve richiamo di quanto abbiamo già dimostrato :
C
• siccome l’eccitazione non è sinusoidale, non si possono usare le impedenze per I (t )
risolvere il circuito. • si scrive l’equazione della maglia, tenendo conto delle relazioni tra corrente e dI
Q(t )
tensione per i diversi componenti (R, L, C): V (t )  L dt (t )  RI (t )  C
• derivando rispetto a t si ottiene:
dI I
d 2I
dV
L 2 R 
• equazione differenziale lineare del dt C
dt
dt
secondo ordine, valida per qualsiasi V(t).
dI I
d 2I
dV
L 2 R 
dt
dt C
dt
• L’equazione è non omogenea. La soluzione è la somma dell’ integrale generale dell’ omogenea più un integrale particolare della disomogenea.
2
d I
dI I
L 2 R  0
dt C
dt
Omogenea associata
• Fisicamente la soluzione dell’ omogenea corrisponde al comportamento transitorio iniziale; a regime vale l’ integrale particolare.
dI I
d 2I
L 2 R  0
dt
dt C
• La soluzione dell’ omogenea è del tipo
k1t
k 2t
I (t )  I1e  I 2 e
• Con I1 e I2 costanti da determinare dalle condizioni iniziali e k1 e k2 soluzioni dell’ equazione caratteristica:
1
Lk  Rk   0
C
2
• quindi
2
k1, 2
1
R
R



2
2L
4 L LC
R2
1

2
4 L LC
• ponendo
R
a
2L
b
• e definendo
R

L
1
 o2
LC
• si trova la soluzione I (t )  I1e  ( a b ) t  I 2 e  ( a b ) t
• La quantità b può essere reale, nulla, o immaginaria, a seconda che sia:
Soluzione complessiva per Q(0)=qo , I(0)=0
 R2
1
 2 
 4 L2 LC
1
R
 2 
 4 L2 LC
R  1
 4 L2 LC
b reale e positivo, caso sovrasmorzato
qoo at bt bt
e {e  e }
I (t )  
2b
b nullo, caso criticamente smorzato
I (t )  qoo te  at
b immaginario, caso sottosmorzato, dove   2RL  
I (t ) 
2
2
1
R2

LC 4 L2
q o o2

e t sen (  t )
• Nell’esperienza osserveremo con l’oscilloscopio la tensione ai capi del resistore, variando il valore di R per ottenere i tre comportamenti. Infatti per avere ad esempio il caso sovrasmorzato dovremo avere
2
Rtot
1

2
4L
LC
2L
 Rtot 
LC
L
 Rtot  2
C
• dove Rtot rappresenta la resistenza totale presente nel circuito RLC serie, e quindi
Rtot  RGs  RL  R
• Noi lasceremo e costanti, e varieremo R, la resistenza RL
RGs
ai capi della quale misureremo la tensione. Otterremo quindi 2
nei tre casi:
qoo  at bt
V (t )  RI (t )   R
e {e  e bt }
2b
R  2 L / C

R  2 L / C
R  2 L / C

V (t )  RI (t )   Rqoo te
2
V (t )  RI (t )  R
q o o2

 at
e t sen (  t )
Esperienza del 20/5/2015
Circuito RLC con segnali impulsivi
• Lo scopo dell’esperienza è verificare il comportamento sottosmorzato, criticamente smorzato e sovrasmorzato dei circuiti RLC serie visibili a fianco, quando il segnale in ingresso è un impulso ad onda quadra. • All’inizio dell’esperienza (circuito 1, uscita ai capi della resistenza) si sostituirà la resistenza R con un potenziometro (resistenza variabile) e si osserverà sull’oscilloscopio, all’aumentare del valore di R, il passaggio dal regime oscillatorio sottosmorzato a quello impulsivo sovrasmorzato.
• Le forme d’onda che si osserveranno sono le seguenti. 1 ‐ Uscita ai capi del resistore R
10
30
50
70
90
130
170
210
caso sottosmorzato
RsG=10
RL=10
L=1mH
C=47nF
R=10… 210
Vo=+5V
1 ‐ Uscita ai capi del resistore R
10
30
50
70
90
130
170
210
caso sottosmorzato
All’aumentare di R si s
RG=10
passa da un regime RL=10
oscillatorio a un regime L=1mH
sempre più impulsivo, C=47nF
aumentando via via R=10… 210 l’ampiezza dell’impulso, Vo=+5V
fino al caso criticamente smorzato (linea tratteggiata). 1 ‐ Uscita ai capi del resistore R
caso sovrasmorzato
300
550
RsG=10
RL=10
L=1mH
C=47nF
R=300… 550
Vo=+5V
Aumentando ulteriormente R si oltrepassa il caso criticamente smorzato e si passa al regime sovrasmorzato, aumentando l’ ampiezza e la larghezza dell’ impulso. Esperienza del 20/5/2015
Circuito RLC con segnali impulsivi
• Il caso criticamente smorzato si ottiene quando le due soluzioni dell’equazione caratteristica sono coincidenti, cioè quando
Rtot

2L
1
LC
 Rtot  2
L
C
• E quindi
R  Rtot  RGs  RL  2
L
 RGs  RL
C
• Si ruota l’asse del potenziometro finchè non si visualizza sull’oscilloscopio un impulso di minima durata e senza ulteriori oscillazioni: questa sarà la condizione di smorzamento critico. Senza muovere l’asse, si scollega il potenziometro dal circuito e se ne misura la resistenza R, controllando che coincida entro gli errori con quello dato dalla formula sopra. Conviene rifare più volte la procedura, per stimare l’incertezza su R.
1
2
3
1
3
2
1
2 3
R
Nota : Importanza del caso criticamente smorzato
• La risposta criticamente smorzata è quella che arriva al valore di regime più rapidamente, senza però introdurre oscillazioni. • E’ importante ottenerla nei sistemi di controllo, nei quali uno o più sensori misurano una quantità fisica, ed il loro segnale viene utilizzato, processandolo opportunamente, per regolarla in tempo reale.
• Il segnale del sensore viene confrontato con il segnale desiderato, e la differenza tra i due viene processata introducendo una componente Proporzionale (amplificazione), una Integrale, una Differenziale (PID). Il segnale differenza, processato PID, viene utilizzato per azionare un attuatore, che regola la quantità fisica di interesse finchè il suo valore non è pari a quello desiderato ( a quel punto la differenza si annulla e l’attuatore si ferma). Valore desiderato
Quantità fisica
sensore
+ Segnale
differenza
PID
Segnale differenza
processato
attuatore
Nota : Importanza del caso criticamente smorzato
• Questo sistema di controllo è un tipo di feedback loop (anello di retroazione), perché la quantità che si vuole regolare, che è una uscita del sistema, viene riutilizzata, misurata dal sensore, per la regolazione della stessa. Viene rimandata indietro, in pasto al regolatore (feedback). La retroazione viene usata comunemente in moltissimi circuiti e sistemi, come si vedrà dopo. Valore desiderato
sensore
+ -
Quantità fisica
Feedback loop
PID
attuatore
• In questo ed in moltissimi altri casi è importante che la risposta del segnale del sensore processato sia più veloce possibile, ma senza oscillazioni. Si deve quindi ottenere un segnale di ingresso all’attuatore processato in modo da realizzare la condizione di smorzamento critico. Nota : Importanza del caso criticamente smorzato
•
Ad esempio: un potenziometro (sensore) viene ruotato dal movimento di una piattaforma girevole, quindi la sua resistenza misura l’angolo di rotazione della piattaforma (osservabile). Il segnale proveniente dal potenziometro viene confrontato con quello desiderato. Il segnale differenza viene processato PID ed utilizzato per comandare il motore (attuatore) che fa ruotare la piattaforma, variandone l’angolo in modo da arrivare all’angolo di rotazione voluto, e in modo da reagire ad eventuali perturbazioni esterne che lo farebbero variare. Valore desiderato
potenziometro
+ -
Feedback loop
PID
•
Angolo piattaforma
motore
Il segnale processato PID deve avere smorzamento critico in modo da arrivare all’angolo desiderato il più velocemente possibile, evitando però oscillazioni della piattaforma. Nota : Importanza del caso criticamente smorzato
• Altro esempio: la lancetta del tester analogico, con la sua molla di richiamo, è un oscillatore meccanico smorzato, che deve essere utilizzato in regime di smorzamento critico per raggiungere la posizione di equilibrio nel più breve tempo possibile, senza oscillarci intorno, per leggere il risultato della misura nel più breve tempo possibile.
Esperienza del 20/5/2015 : Circuito RLC con segnali impulsivi
• Nella seconda parte dell’esperienza si studia la tensione ai capi del condensatore, in regime sottosmorzato. • Se consideriamo l’equazione omogenea per la carica (lezione 9):
dI
Q(t )
0  L (t )  RI (t ) 
dt
C

d 2Q
dQ Q(t )
 0  L 2 (t )  R

dt
dt
C
d 2Q
dQ
2




oQ  0
2
dt
dt
• L’equazione caratteristica e le sue soluzioni sono  
      0         o2
2
2
2
2
o
• E quindi, nel caso sottosmorzato
Q  Qo e

 t
2
cos 1t

2
smorzamento
Qo  2 t
 VC (t ) 
e cos 1t
C
pseudoperiodo
Esperienza del 20/5/2015
Circuito RLC con segnali impulsivi
• Nella seconda parte dell’esperienza (circuito 2, con uscita ai capi del condensatore, che si ottiene dal precedente scambiando condensatore e resistore) si lavorerà in regime sottosmorzato, inserendo al posto del potenziometro R una resistenza fissa da 10. • Scopo di questa parte è la misura dello smorzamento e dello pseudo‐
periodo. • Si visualizzerà l’ oscillazione smorzata, ottimizzando le impostazioni dell’oscilloscopio per riempire il più possibile lo schermo. • Si prenderanno poi tempi e ampiezze dei massimi successivi dell’oscillazione. con shunt
T1 
2
1
Linea sottile: con shunt
R=10, RL=10, RG=10, L=1mH, C=10nF
Linea spessa: senza shunt
R=10, RL=10, RG=50, L=1mH, C=10nF
V  Vo e
 t / 2
VC  Vo e  t / 2 cos(1t )
Dalla sequenza dei massimi, graficando i dati in scala semilog, si può ricavare .
Dalla distanza tra i massimi, si può ricavare 
T1 
VC  Vo e  t / 2 cos(1t )
2
1