INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
Calcolo retta Regressione Lineare utilizzando il
metodo dei minimi quadrati
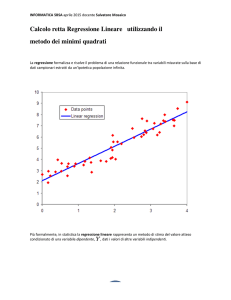
La regressione formalizza e risolve il problema di una relazione funzionale tra variabili misurate sulla base di
dati campionari estratti da un'ipotetica popolazione infinita.
Più formalmente, in statistica la regressione lineare rappresenta un metodo di stima del valore atteso
condizionato di una variabile dipendente, , dati i valori di altre variabili indipendenti.
INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
Metodo dei MINIMI QUADRATI
Si tratta di approssimare il fenomeno con una retta y=mx+qi cui coefficienti si ricavano dalla relazione
n(∑ xi yi ) − (∑ xi )(∑ yi )
m=
2
2
n ∑ xi − (∑ xi )
(
)
(
x )(∑y ) − (∑x )(∑x y )
∑
q=
2
i
i
i
i i
n(∑xi ) − (∑xi )
2
2
Che può essere più semplicemente scritta (dal punto di vista dei calcoli)
y − m∑x
∑
q=
i
i
n
L’analisi della correlazione fra due variabili conduce a misurare la forza, o l’intensità, del legame
fra le due variabili. Si misura mediante l’indice di Bravais-Pearson detto “Indice di correlazione
lineare”
2
INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
r=
n∑xi yi − ∑xi ∑yi
n∑xi − (∑xi ) * n∑yi − (∑yi )
2
2
2
2
Frammento di codice che fa i calcoli in javascript
SOMMATORIAX = 0;
SOMMATORIAY = 0;
SOMMATORIAXX = 0;
SOMMATORIAXY = 0;
SOMMATORIAYY = 0;
for (i = 1; i <= N; i++)
SOMMATORIAX = SOMMATORIAX +
SOMMATORIAY = SOMMATORIAY +
SOMMATORIAXY = SOMMATORIAXY
SOMMATORIAXX = SOMMATORIAXX
SOMMATORIAYY = SOMMATORIAYY
// per ciascun punto
{
X[i];
Y[i];
+ X[i] * Y[i];
+ X[i] * X[i];
+ Y[i] * Y[i];
} // i = 1 to 16
PENDENZA = (N * SOMMATORIAXY - SOMMATORIAX * SOMMATORIAY) / (N * SOMMATORIAXX SOMMATORIAX * SOMMATORIAX);
QUOTA = (SOMMATORIAY - PENDENZA * SOMMATORIAX) / N;
r = (N * SOMMATORIAXY - SOMMATORIAX * SOMMATORIAY) / (pow(N * SOMMATORIAXX - SOMMATORIAX *
SOMMATORIAX, 0.5) * pow(N * SOMMATORIAYY - SOMMATORIAY * SOMMATORIAY, 0.5));
Esempio
Riportiamo i valori della differenza di potenziale V , ottenuti facendo variare la differenza di
potenziale ai capi di un conduttore (misurata in Volt, con un errore assoluto di (0,1V) e misurando
la corrispondente intensità di corrente I (misuarta in milliampere, con un errore di 0,2Ma)
Osservando la distribuzione dei punti ci aspettiamo una relazione lineare che andiamo a calcolare
Col metodo sopra descritto
3
INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
Dopo avere calcolato abbiamo m e q possiamo calcolare i valori teorici
INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
Una volta ottenuta la funzione si può vedere il valore teorico calcolato
Vediamo infine alcuni esercizi
INFORMATICA 5ASA aprile 2015 docente Salvatore Mosaico
1) Pressione Arteriosa
Data una popolazione di individui si vuole stimare la relazione tra pressione arteriosa ed età.
La seguente tabella riporta i dati relativi al campionamento:
ETA'
PRESSIONE
25
120
30
125
42
135
55
140
55
145
69
180
70
160
Si ipotizza una relazione lineare tra le grandezze del tipo:
y = ax + b
Si richiede di stimare i coefficienti della retta mediante il metodo dei minimi quadrati.
2) Fatturato
La seguente tabella riporta i dati relativi al fatturato degli ultimi cinque anni di una nota
azienda di giocattoli (il fatturato è espresso in milioni di Euro):
ANNO
FATTURATO
(106 €)
1
9
2
11,2
3
9,8
4
11,8
5
14
Si determini un modello di regressione lineare semplice per prevedere l'andamento futuro del
fatturato.
6