docx - Luca Ghio

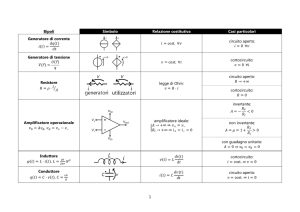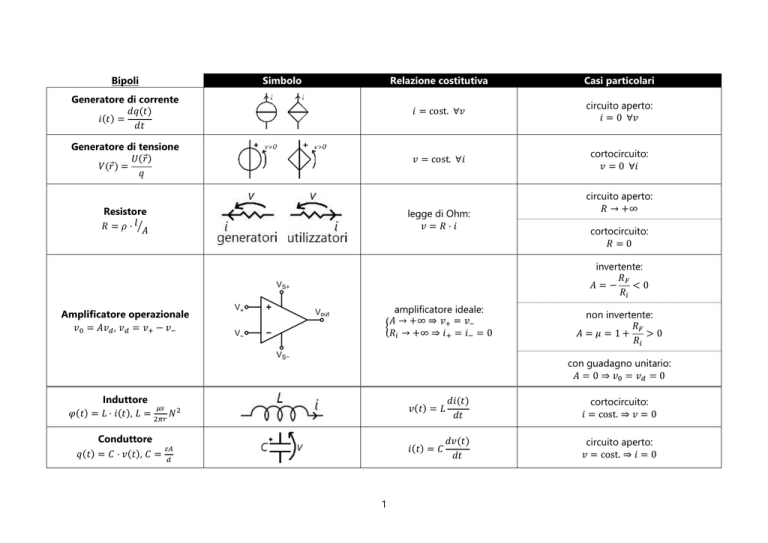
Bipoli
Simbolo
Relazione costitutiva
Casi particolari
Generatore di corrente
𝑑𝑞(𝑡)
𝑖(𝑡) =
𝑑𝑡
𝑖 = cost. ∀𝑣
circuito aperto:
𝑖 = 0 ∀𝑣
Generatore di tensione
𝑈(𝑟⃗)
𝑉(𝑟⃗) =
𝑞
𝑣 = cost. ∀𝑖
cortocircuito:
𝑣 = 0 ∀𝑖
Resistore
𝑅 = 𝜌 ⋅ 𝑙⁄𝐴
legge di Ohm:
𝑣 =𝑅⋅𝑖
circuito aperto:
𝑅 → +∞
cortocircuito:
𝑅=0
invertente:
𝑅𝐹
𝐴=−
<0
𝑅𝑖
Amplificatore operazionale
𝑣0 = 𝐴𝑣𝑑 , 𝑣𝑑 = 𝑣+ − 𝑣−
amplificatore ideale:
𝐴 → +∞ ⇒ 𝑣+ = 𝑣−
{
𝑅𝑖 → +∞ ⇒ 𝑖+ = 𝑖− = 0
non invertente:
𝑅𝐹
𝐴 =𝜇 =1+
>0
𝑅𝑖
con guadagno unitario:
𝐴 = 0 ⇒ 𝑣0 = 𝑣𝑑 = 0
Induttore
𝜇𝑠
𝜑(𝑡) = 𝐿 ⋅ 𝑖(𝑡), 𝐿 = 2𝜋𝑟 𝑁 2
𝑣(𝑡) = 𝐿
𝑑𝑖(𝑡)
𝑑𝑡
cortocircuito:
𝑖 = cost. ⇒ 𝑣 = 0
Conduttore
𝜀𝐴
𝑞(𝑡) = 𝐶 ⋅ 𝑣(𝑡), 𝐶 = 𝑑
𝑖(𝑡) = 𝐶
𝑑𝑣(𝑡)
𝑑𝑡
circuito aperto:
𝑣 = cost. ⇒ 𝑖 = 0
1
Rappresentazioni
dei doppi bipoli
Relazione
costitutiva
𝑅11 =
su base corrente
𝑣1 , 𝑣2 = 𝑓(𝑖1 , 𝑖2 )
𝑣1
𝑖
(𝑣 ) = 𝑅 ( 1 )
𝑖2
2
Condizione
di reciprocità
Matrice
𝑅21 =
𝑣1
⁄𝑖 |
1 𝑖
2 =0
𝑣2
⁄𝑖 |
1 𝑖
2 =0
𝑅12 =
2 =0
su base tensione
𝑖1 , 𝑖2 = 𝑓(𝑣1 , 𝑣2 )
𝑣1
𝑖
( 1 ) = 𝐺 (𝑣 )
𝑖2
2
𝐺21
𝑖
= 2⁄𝑣1 |
𝑣
2 =0
𝑅22 =
ibrida
𝑣1 , 𝑖2 = 𝑓(𝑖1 , 𝑣2 )
𝑣1
𝑖
(𝑖 ) = 𝐻 ( 1 )
𝑣2
2
𝑣1
⁄𝑖 |
1 𝑣
2 =0
(resistenza equivalente)
𝐻21
𝑖
= 2⁄𝑖 |
1 𝑣
2 =0
(guadagno in corrente)
di trasmissione
𝑣1 , 𝑖1 = 𝑓(𝑣2 , −𝑖2 )
𝑇11 = 𝐴 =
𝑣1
𝑣2
( 𝑖 ) = 𝑇 (−𝑖 )
1
2
𝑇21
𝑣1
⁄𝑣2 |
𝑖
2 =0
𝑖
= 𝐶 = 2⁄𝑣2 |
𝑖
2 =0
2
𝑅21 = 𝑅12
𝑣2
⁄𝑖 |
2 𝑖
1 =0
𝑖
𝐺12 = 1⁄𝑣2 |
𝑣
1 =0
(trans-conduttanza)
𝐺22
(trans-conduttanza)
𝐻11 =
1 =0
(trans-resistenza)
(trans-resistenza)
𝑖
𝐺11 = 1⁄𝑣1 |
𝑣
𝑣1
⁄𝑖 |
2 𝑖
𝐺21 = 𝐺12
𝑖
= 2⁄𝑣2 |
𝑣
𝐻12 =
1 =0
𝑣1
⁄𝑣2 |
𝑖
1 =0
(guadagno in tensione)
𝐻12 = −𝐻21
𝑖
𝐻22 = 2⁄𝑣2 |
𝑖
1 =0
(conduttanza equivalente)
𝑇12 = 𝐵 =
𝑇22
𝑣1
⁄−𝑖 |
2 𝑣
2 =0
𝑖
= 𝐷 = 1⁄−𝑖 |
2 𝑣
2 =0
det(𝑇) = 1
Legge di Ohm
(nel dominio dei fasori)
𝑉 =𝑍⋅𝐼
𝐼 =𝑌⋅𝑉
𝑍 = 𝑅 + 𝑗𝑋 (impedenza)
𝑌 = 1⁄𝑍 = 𝐺 + 𝑗𝐵 (ammettenza)
𝑉𝑀
⁄𝐼 (resistenza)
𝑀
• Im{𝑍} = 𝑋 = 𝜃𝑣 − 𝜃𝑖 (reattanza)
• Re{𝑍} = 𝑅 =
𝑅
𝐼
= 𝑀⁄𝑉 (conduttanza)
𝑅2 +𝑋 2
𝑀
𝑋
− 2 2 = 𝜃𝑖 − 𝜃𝑣 (suscettanza)
𝑋 +𝑅
• Re{𝑌} = 𝐺 =
• Im{𝑌} = 𝐵 =
Bipoli resistivi
𝑋=0
{
𝐵=0
𝑌=𝐺
resistore
𝑍=𝑅
𝑍=
condensatore
Bipoli reattivi
𝑅=0
{
𝐺=0
induttore
1
= 𝑗𝑋𝐶
𝑗𝜔𝐶
1
𝑋𝐶 = −
𝜔𝐶
𝑍 = 𝑗𝜔𝐿 = 𝑗𝑋𝐿
𝑋𝐿 = 𝜔𝐿
3
𝐺=
1
𝑅
𝑌 = 𝑗𝜔𝐶 = 𝑗𝐵𝐶
𝐵𝐶 = −
𝑌=
1
= 𝜔𝐶
𝑋𝐶
1
= 𝑗𝐵𝐿
𝑗𝜔𝐿
𝐵𝐿 = −
1
1
=−
𝑋𝐿
𝜔𝐿
1
2
𝑆 = 𝑉𝐼 ̅ = 𝑃 + 𝑗𝑄 (potenza complessa)
Potenza
(in regime sinusoidale)
resistore
𝑃>0
condensatore
𝑄<0
induttore
𝑄>0
|𝑆| = 𝑉eff ⋅ 𝐼eff (potenza apparente)
cos ∠𝑆 = cos(𝜃𝑣 − 𝜃𝑖 ) = cos 𝜑 (fattore di potenza)
Re{𝑆} = 𝑃 = 𝑉eff 𝐼eff cos 𝜑 (potenza attiva)
Im{𝑆} = 𝑄 = 𝑉eff 𝐼eff sen 𝜑 (potenza reattiva)
2
𝑃 = 𝑅𝐼eff
2
𝑃 = 𝐺𝑉eff
2
𝑃 = 𝑅𝐼eff
2
𝑃 = 𝐺𝑉eff
2
𝑄 = 𝑋𝐼eff
𝑋=0
⇒𝑄=0
{
𝐵=0
𝑄=−
𝑅=0
⇒𝑃=0
{
𝐺=0
1 2
𝐼
𝜔𝐶 eff
2
𝑄 = 𝜔𝐿𝐼eff
4
2
𝑄 = −𝐵𝑉eff
2
𝑄 = −𝜔𝐶𝑉eff
𝑄=
1 2
𝐼
𝜔𝐿 eff
Circuiti RLC in evoluzione libera
𝑥(𝑡) = 𝐴1 𝑒 𝑠1 𝑡 + 𝐴2 𝑒 𝑠2 𝑡
2
𝑑 𝑥
𝑑𝑥
+ 2𝛼
+ 𝜔0 2 𝑥 = 0
2
𝑑𝑡
𝑑𝑡
{
𝑠1 = −𝛼 + √𝛼 2 − 𝜔0 2
𝑠2 = −𝛼 − √𝛼 2 − 𝜔0 2
sovrasmorzato
𝛼 > 𝜔0
𝑥(𝑡) = 𝐴1 𝑒 𝑠1 𝑡 + 𝐴2 𝑒 𝑠2 𝑡
𝑠2 < 𝑠1 < 0
con smorzamento critico
𝛼 = 𝜔0
𝑥(𝑡) = (𝐴1 𝑡 + 𝐴2 )𝑒 −𝛼𝑡
𝑠1 = 𝑠2 = −𝛼 = −𝜔0
sottosmorzato
0 < 𝛼 < 𝜔0
senza smorzamento
𝛼=0
𝑥(𝑡) = [𝐴1 cos(𝛽𝑡) + 𝐴2 sen(𝛽𝑡)]𝑒 −𝛼𝑡
con 𝛽 = √𝜔0 2 − 𝛼 2
𝑥(𝑡) = 𝐴1 cos(𝜔0 𝑡) + 𝐴2 sen(𝜔0 𝑡)
5
{
𝑠1 = −𝛼 + 𝑗√𝜔0 2 − 𝛼 2
𝑠2 = −𝛼 − 𝑗√𝜔0 2 − 𝛼 2
{
𝑠1 = +𝑗√𝜔0 2 − 𝛼 2
𝑠2 = −𝑗√𝜔0 2 − 𝛼 2
Filtri in regime sinusoidale
|𝑯(𝒋𝝎)| (risposta in ampiezza della funzione di trasferimento)
circuito RC
passa-alto
𝐻(𝑗𝜔) =
𝑉𝑅
𝑗𝜔𝑅𝐶
=
𝑉𝑖 1 + 𝑗𝜔𝑅𝐶
circuito RL
𝜔𝐶 =
1
𝑅𝐶
circuito RC
passa-basso
𝐻(𝑗𝜔) =
𝑉𝐶
1
=
𝑉𝑖 1 + 𝑗𝜔𝑅𝐶
𝑍(𝑗𝜔) =
𝑉𝑜
1
=
𝑉𝑖 1 + 𝑗 (𝜔𝐶 − 1 )
𝑅
𝜔𝐿
circuito RL
passa-banda
circuito RLC parallelo
𝜔0 =
1
√𝐿𝐶
𝑄 = 𝜔0 𝑅𝐶
elimina-banda
𝑌(𝑗𝜔) =
circuito RLC serie
6
𝐼𝑜
1
=
𝑉𝑖 𝑅 + 𝑗 (𝜔𝐿 − 1 )
𝜔𝐶
Trasformata di Laplace
+∞
𝐹(𝑠) = ℒ[𝑓(𝑡)] = ∫
𝑓(𝑡)𝑒 −𝑠𝑡 𝑑𝑡
0
riscalamento
ℒ[𝑘𝑓(𝑡)] = 𝑘𝐹(𝑠)
linearità
ℒ[𝑓1 (𝑡) + 𝑓2 (𝑡)] = 𝐹1 (𝑠) + 𝐹2 (𝑠)
derivazione
rispetto al tempo
ℒ[
derivazione
rispetto a 𝒔
𝑑𝑓(𝑡)
] = 𝑠𝐹(𝑠) − 𝑓(0)
𝑑𝑡
ℒ[𝑡 ⋅ 𝑓(𝑡)] = −
𝑑𝐹(𝑠)
𝑑𝑠
traslazione
rispetto al tempo
ℒ[𝑢(𝑡 − 𝑡0 ) ⋅ 𝑓(𝑡 − 𝑡0 )] = 𝑒 −𝑠⋅𝑡0 𝐹(𝑠)
trasformata
di funzioni periodiche
𝑓(𝑡) periodica di periodo 𝑇:
1
ℒ[𝑓(𝑡)] = 𝐹(𝑠)
1 − 𝑒 −𝑠𝑇
ℒ[𝑒 𝑎𝑡 ] =
7
1
𝑠−𝑎