CORRENTE ALTERNATA IN Un RESISTORE

CIRCUITI IN CORRENTE ALTERNATA
Più del 99% dell’energia elettrica prodotta e consumata è alternata perché con un trasformatore
posso alzate la tensione e di conseguenza far scendere la corrente così non si scaldano troppo i fili.
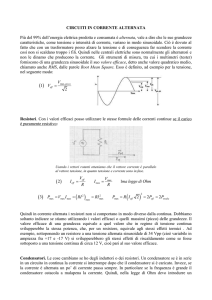
Gli strumenti di misura forniscono il valore efficace (valore quadratico medio RMS) di una
grandezza sinusoidale.
1
I eff 
I max
2
Con i valori efficaci posso utilizzare le stesse formule delle correnti continue se il carico è
puramente resistivo:
 2
Pmedia   RI 2 
 3
I eff 
Veff
R
medio

1 2
RI  Veff I eff
2
legge di Ohm
Quindi in corrente alternata i resistori non si comportano in modo diverso dalla continua.
Condensatori
Le cose cambiano se ho degli induttori o dei resistori.
Un condensatore se è in serie in un circuito in continua la corrente si interrompe dopo che il
condensatore si è caricato.
Invece, se la corrente è alternata un po’ di corrente passa sempre. In particolare se la frequenza è
grande il condensatore ostacola a malapena la corrente. Quindi nella legge di Ohm devo introdurre
un termine che dipende dalla frequenza:
 4
I eff 
Veff
XC
XC 
1
1

C 2 fC
reat tan za capacitiva
Maggiore è la frequenza minore è la reattanza.
Si può dimostrare che la potenza media in un condensatore è nulla. Quindi un condensatore a
differenza di un resistore non dissipa energia ma la accumula.
Induttore
Con una corrente continua l’induttore è semplicemente un pezzo di filo. Se la corrente è variabile si
genera una fem indotta che è direttamente proporzionale alla rapidità di variazione della corrente
cioè alla frequenza. Quindi ad alta frequenza l’induttore ostacola la corrente.
 5
I eff 
Veff
X C   L  2 fL reat tan za induttiva
XL
RLC circuito serie
Poiché la reattanza induttiva aumenta all’aumentare della frequenza mentre quella capacitiva
diminuisce in un circuito dove ci sono tutti e due può capitare che si uguagliano:
2 fL 
X L  XC
1
2 fC

f 
1
2 LC
frequenza di risonanza
Chiamo impedenza Z la grandezza:
 6
Z  R2   X L  X C 
7
I max 
8
I eff 
8'
1
Pmedia  Veff I eff cos   Vmax I max cos 
2
tan  
2
Vmax
R2   X L  X C 
Veff
Z
2

X L  XC
R
Vmax
Z
sin t   
L’impedenza è minima e la corrente efficace è massima se la frequenza della fem è uguale alla
frequenza di risonanza. Inoltre la tensione è minima.
Nella realtà il circuito risonante a causa delle perdite provocate dai componenti e dal carico si ha
una diminuzione della condizione di risonanza. Per questo si introduce il fattore di merito Q.
9
Q
2 fL
R
Tanto più alto è tale valore quanto più selettivo è il circuito
Se il circuito è abbastanza risonante, cioè per Q maggiore di 23 tale fattore può essere arrotondato
a:
10 
Q
f
f
f è la larghezza a meta altezza della curva di risonanza.
RLC circuito parallelo
Quando la frequenza della tensione di alimentazione di un circuito accordato di tipo “ in parallelo” è
uguale a quella di risonanza del circuito la tensione raggiunge i valori massimi e la corrente quelli
minimi perché l’impedenza è massima.
In un circuito radio il valore di L e di C (variabile) seleziona la frequenza del segnale catturato. A
valle avrò il segnale di tensione massimo. Quando invece in un circuito debbo fare delle regolazioni
fini di taratura è preferibile avere un’induttanza variabile costituita da una bobina munita di nucleo
di ferrite.
Ricevitore a galena